Лекция 6. Примеры программ с циклическим алгоритмом.

Вывод по формату.

Решение практических задач сводится к использованию некоторого набора типовых приемов, облегчающих процесс программирования. Рассмотрим наиболее часто встречающиеся задачи с использованием циклического алгоритма.

Табулирование функции

Первый пример – табулирование функции – был подробно рассмотрен в предыдущей лекции и здесь на нем не будем останавливаться, см. Лекцию 5 данного курса.

Вычисление суммы конечного числа слагаемых (алгоритм накопления суммы)

Рассмотрим сумму конечного числа слагаемых:

(1)

Здесь a_n – слагаемое или общий член суммы с номером n. n меняется в данной сумме от значения p до значения q с шагом 1. В математике принята следующая сокращенная запись такой суммы:

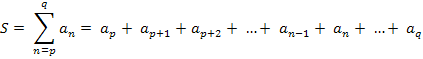
Здесь a_n - слагаемое или общий член суммы с номером (индексом суммирования) n. n – номер слагаемого в сумме, p - номер первого слагаемого в сумме, q – номер последнего слагаемого в сумме. Вычислять данную сумму будем последовательно, добавляя очередное слагаемое к ранее вычисленному значению суммы.

Алгоритм накопления суммы:

(3)

Пусть вычислено значение суммы S_n-1 первых слагаемых от p-того до (n-1)-го слагаемого включительно, тогда следующее значение суммы с добавлением следующего слагаемого a_n будет равно S_n = S_n-1 + a_n.

Это так называемый алгоритм накопления суммы, аналогичный алгоритму накопления определенной суммы денег на счете банковской карты: каждое последующее перечисление денег увеличивает сумму на величину перечисленных денег.

Так как при вычислении на компьютере не обязательно сохранять каждое вычисленное значение суммы в отдельных ячейках памяти, то для хранения значения суммы выделим одну ячейку памяти S, и в расчетных формулах опустим индексы (номера),

S=S+a – рекуррентная формула накопления суммы: каждое последующее значение суммы вычисляется через предыдущее. Как правило, начальное значение S=0 (S_n-1=0, при n=1).

Рассмотрим подробнее на конкретном примере.

Пример 1. Вычислить значение суммы .

Б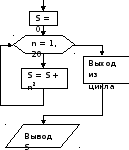лок-схема задачи:

Запишем программу:

program SUM1

S = 0

do n=1, 20

S = S + n**2

enddo

print *,’ S=’,S

end

При решении используем принцип накопления, при котором вычисленное слагаемое в цикле прибавляется к сумме всех предыдущих, т.е. . Здесь S_n и S_n-1 надо представить в виде простых переменных, поэтому оператор присваивания, накапливающий сумму, должен иметь вид (a_n = n²). Параметр цикла n одновременно является и индексом суммирования. Перед первым выполнением оператора цикла, начальное значение S должно быть равно нулю. Следовательно, перед циклом должен стоять оператор присваивания S = 0, а оператор внутри тела цикла – накапливает сумму.

Рассмотрим данную программу «по шагам». В этом примере находим сумму , т.е. S_n = S₁ + S₂ + S₃ + … + S₂₀ = 1² + 2² + 3² + 4² + … + 20² = 1 + 4 + 9 + 16 + … + 400. Таким образом,

Шаг 1. S присваивается значение, равное 0 (S = 0).

Шаг 2. Счетчику цикла n присваивается начальное значение n = 1 при первом проходе цикла.

Шаг 3. Рассчитывается новое значение переменной S = 0 + 1² = 1 (добавлено первое слагаемое).

Шаг 4. На 2-ом проходе цикла n становится равным 2 (n = 2) и в цикле происходит добавление следующего слагаемого в переменную S: S = 1 + 2² = 5 (сумма двух слагаемых).

Шаг 5. На 3-ем проходе цикла n = 3, S становится равной S = 5 + 3² = 14 (сумма трех слагаемых).

и т.д. до последнего прохода цикла. Последний раз в переменную S добавится последнее слагаемое 20² = 400 (n = 20) и сумма полностью посчитается. Цикл завершится.

Последний шаг. Вывод значения суммы S.

Заметим, что начальное значение переменной суммы до цикла задается равным нулю для того, чтобы при первом проходе цикла в переменную S не добавилось ничего лишнего к результирующей сумме. По правилам оператора присваивания, сначала вычисляется выражение, находящееся справа от знака равенства, т.е. S + a, а потом вычисленный результат присваивается переменной, стоящей слева от знака равенства, т.е. переменной S присваивается новое значение, увеличенное на слагаемое a. Т.е. если сначала S ≠ 0, то это число добавится в сумму и окончательный результат будет неверным.