11

Министерство общего и профессионального образования

Российской Федерации

Комсомольский-на-Амуре государственный

технический университет

Кафедра «Электропривод и автоматизация промышленных установок»

ИССЛЕДОВАНИЕ ВРЕМЕННЫХ И ЧАСТОТНЫХ ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ

Методические указания к лабораторным работам по курсу

«Теория автоматического управления»

Комсомольск-на-Амуре 2004

Цель работы: изучение передаточных функций, переходных функций и функций веса типовых звеньев, а также амплитудно-фазовых, логарифмических амплитудной и фазовой частотных характеристик типовых звеньев; исследование влияния параметров типовых звеньев на частотные и временные характеристики.

1 Основные теоретические положения

1.1 ПЕРЕДАТОЧНАЯ ФУНКЦИЯ

Физические процессы в любой динамической системе в общем случае описываются системой дифференциальных уравнений, которая может быть сведена к одному дифференциальному уравнению в форме Коши

,

где x_вх(t) – входное воздействие;

x_вых(t) – изменение выходной величины;

a_i, b_i, i = 1..n, j = 1..m – постоянные величины, которые определяются физическими свойствами системы.

При замене знака производной оператором дифференцирования , дифференциальное уравнение запишется в виде операторного уравнения

.

В теории автоматического управления (ТАУ) широкое применение получил способ математического описания динамических систем, основанный на использовании передаточной функции, которая определяется из операторного уравнения.

.

Передаточной функцией системы автоматического управления (САУ) называют отношение преобразования Лапласа выходной величины x_вых(p) к преобразованию Лапласа входного воздействия x_вх(p) при нулевых начальных условиях. Как правило для физической реализации порядок числителя должен быть меньше или равен порядку знаменателя m  n. При этом порядок знаменателя m является порядком САУ.

При анализе динамических свойств САУ рассматривается как звено (см. рис. 1) с передаточной функцией W(p), имеющее входное воздействие x_вх(t) и выходную величину x_вых(t). Передаточная функция полностью характеризует динамические свойства системы. Зная передаточную функцию САУ и вид воздействия, можно определить описание переходного процесса на выходе САУ

; ; .

Звенья не выше второго порядка n  2 называются типовыми. Любую сложную по конструктивному исполнению и функциональному назначению, систему можно разбить на типовые звенья. В данной лабораторной работе исследуются шесть типовых звеньев: апериодическое, инерционное 2-ого порядка, интегрирующее, реально-дифференцирующее, интегро-дифференцирующее и запаздывающее.

1.2 Временные характеристики

Важными временными характеристиками типовых звеньев являются переходная и импульсная переходная функции.

Переходная функция h(t) звена есть функция, описывающая реакцию звена на единичное ступенчатое воздействие 1(t) при нулевых начальных условиях. Сигнал 1(t) имеет уравнение

и изображение по Лапласу

.

График единичного ступенчатого воздействия изображён на рис. 2.

Импульсной переходной w(t) или весовой функцией (функцией веса) звена называют функцию, описывающую реакцию звена на единичное импульсное воздействие (t) при нулевых начальных условиях. Функция веса (t) имеет уравнение

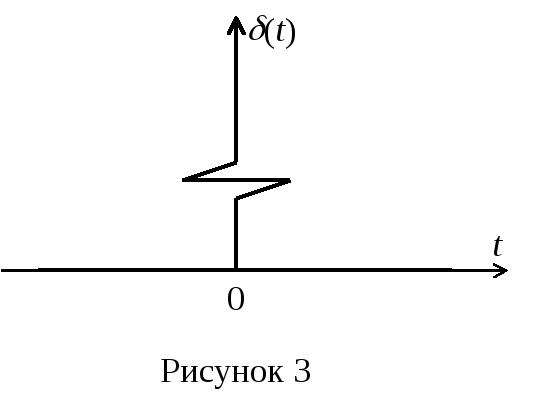
и изображение по Лапласу

.

График весовой функции представлен на рис. 3. Между переходной функцией и функцией веса существует алгебраическая связь

.

Графики переходной функции и функции веса называют соответственно переходной и импульсной переходной характеристикой.

1.3 Частотные характеристики

Частотные характеристики получаются при рассмотрении установившихся процессов на выходе звена при подаче на его вход гармонического воздействия с амплитудой A_вх и частотой . В результате на выходе звена возникает гармонический сигнал с той же частотой , но с другой амплитудой A_вых и со сдвигом фазы  относительно входного сигнала (см. рис. 4). Величины A_вых и  будут изменяться при изменении частоты .

В результате образуются частотные характеристики:

– амплитудная частотная характеристика (АЧХ);

() – фазовая частотная характеристика (ФЧХ).

Уравнения частотных характеристик можно получить из частотной передаточной функции. Частотную передаточную функцию W(j) получают из передаточной функции W(p) при подстановке в неё p = j :

.

Частотная передаточная функция является комплексной функцией от действительной переменной . Поэтому функцию W(j) можно представить в виде

,

где P(), Q() – соответственно вещественная (ВЧХ) и мнимая (МЧХ) частотные характеристики звена;

Характеристики A() и () связаны с характеристиками P() и Q() следующими соотношениями:

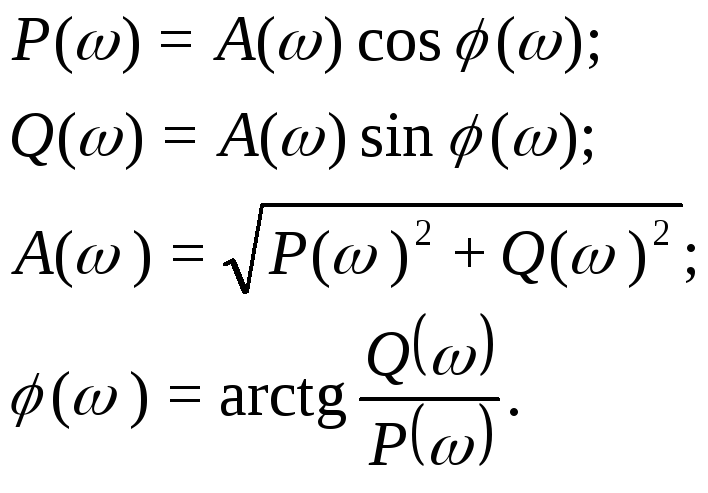
Кривую (см. рис. 5), описываемую концом вектора W(j) на комплексной плоскости (годограф вектора W(j)), называют амплитудно-фазовой частотной характеристикой (АФХ). В этом случае при частоте  значение АЧХ A() = | W(j) | есть модуль комплексного вектора W(j), а значение ФЧХ () = arg W(j) – аргумент комплексного вектора W(j), т. е. угол между вектором W(j) и вещественной осью комплексной плоскости.

При исследовании САУ часто используются логарифмические частотные характеристики.

Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического звена называют кривую, соответствующую 20 десятичным логарифмам модуля передаточной функции W(j) динамического звена, построенной в логарифмическом масштабе частот.

Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют фазовую частотную характеристику (), построенную в логарифмическом масштабе частот.