Задача 2

Плоский механизм состоит из стержней 1 – 4и ползунаВ,соединенных друг с другом и с неподвижными опорамиО₁иО₂шарнирами. Длины стержней: l₁ = 0,4м; l₂ = 1,2м; l₃ = 1,4м;l₄ = 0,8м. Положение механизма определяется угламиα, β, γ, φ, θ,которые вместе с другими величинами заданы в табл. 7.3.

Точка Dна всех схемах и точкаКна схемах 7 – 9 находятся в середине соответствующего стержня. Определить величины, указанные в табл. 7.3. Найти также ускорениеа_AточкиАстержня 1,если стержень 1имеет в данный момент времени угловое ускорениеε₁ =10с^-2.

Стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т.е. по ходу или против хода часовой стрелки (например, угол γна схеме. 1следует отложить от стержняDEпротив хода часовой стрелки, а на схеме 2 – от стержняАЕпо ходу часовой стрелки).

Построение чертежа начинать со стержня, направление которого определяется углом α; ползунВи его направляющие для большей на­глядности изобразить, как в примере (рис. 7.4).Заданную угло­вую скорость считать направленной против хода часовой стрелки, а задан­ную скоростьv_B – от точкиВкb.

Указания.Это задача на исследование плоскопараллельного движе­ния твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновен­ном центре скоростей, применяя эту теорему (или это понятие) к каждо­му звену механизма в отдельности.

Варианты схем к задаче 2

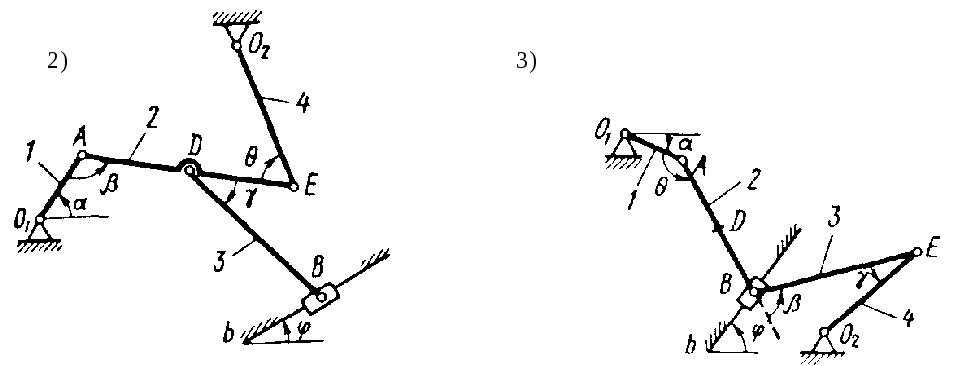
Таблица 7.4

Номер варианта условий	Углы, град.					Дано			Найти
	α	β	γ	φ	θ	ω1, 1/с	ω4, 1/с	vB, м/с
0	30	150	120	0	60	2	—	—	vB, vЕ, ω2
1	60	60	60	90	120	—	3	—	vА, vD, ω3
2	0	120	120	0	60	—	—	10	vА, vЕ, ω2
3	90	120	90	90	60	3	—	—	vB, vЕ, ω2
4	0	150	30	0	60	—	4	—	vB, vА, ω2
5	60	150	120	90	30	—	—	8	vА, vЕ, ω3
6	30	120	30	0	60	5	—	—	vB, vЕ, ω3
7	90	150	120	90	30	—	5	—	vА, vD, ω3
8	0	60	30	0	120	—	—	6	vА, vЕ, ω2
9	30	120	120	0	60	4	—	—	vB, vЕ, ω3

Пример решения задачи 2

Механизм (рис. 7.4, а) состоит из стержней 1, 2, 3, 4 и ползунаВ,соединенных друг с другом и с неподвижными опорамиО₁иО₂шарнирами.

Рис. 7.4

Дано: а = 120°;β = 60°;γ = 90°;φ = 0°;θ = 30°;АD = DE; l₁ = 0,6м;l₂ =1,2м;ω₁= 5c^-1;ε₁ = 8с^-2.

Определить: v_B; v_E; ω₃ и а_А.

Решение

1.Строим положение механизма в соответствии с заданны­ми углами (рис. 7.4, б) .

2.Определяемv_E.ТочкаЕпринадлежит стержнюАЕ.Чтобы найтиv_E,надо знать скорость какой-нибудь другой точки этого стержня и на­правлениеv_E. По данным задачи можем определить:

Вектор .

Направление найдем, учтя, что точкаЕпринадлежит одновременно стержнюО₂Е,вращающемуся вокругО₂;следовательно,.Те­перь, знаяи направление, воспользуемся теоремой о проекциях скоростей двух точек тела (стержняАЕ)на прямую, соединяющую эти точки (прямуюАЕ).Сначала по этой теореме устанавливаем, в какую сторону направлен вектор(проекции скоростей должны иметь одина­ковые знаки).Затем, вычисляя эти проекции, находим:

;

м/с.

3.Определяем. ТочкаВпринадлежит стержнюВD.Следовательно, по аналогии с предыдущим, чтобы определить, надо сначала найти ско­рость точкиD,принадлежащей одновременно стержнюАЕ.Для этого, знаяи, построим мгновенный центр скоростей (МЦС) стержняАЕ; это точкаС₂,лежащая на пересечении перпендикуляров ки, вос­ставленных из точекАиЕ (киперпендикулярны стержни 1и 4). По направлению вектораопределяем направление поворота стержняАЕвокруг МЦСС₂. Векторбудет перпендикулярен отрезкуC₂D, соединяющему точки DиС₂,и направлен в сторону поворота. Величинунайдем из пропорции:

. (1)

Чтобы вычислить C₂DиС₂А,заметим, что ∆АС₂Е – прямоуголь­ный, так как острые углы в нем равны 30°и 60°,и чтоС₂А =АЕsin30° = 0,5АЕ = AD.Тогда ∆АС₂Dявляется равносторонним, иС₂А =С₂D. В ре­зультате равенство (1)дает:

м/с,.

Так как точка Впринадлежит одновременно ползуну, движущему­ся вдоль направляющих поступательно, то направлениеизвестно. Тогда, восстанавливая из точекВ и Dперпендикуляры к скоростями, построим мгновенный центр скоростейС₃стержняBD.По направлению вектораопределяем направление поворота стержня BDвокруг центраС₃.Векторбудет направлен в сторону поворота стержня BD.Из рис. 7.4,б видно, чтоC₃DB = 30°,aDC₃B = 90°,откудаС₃B = l₃sin 30°,C₃D =l₃cos 30°. Составив теперь пропорцию, найдем, что

;

м/с.

4.Определяемω₃. Так как мгновенный центр скоростей стержня 3известен (точкаС₃),то

5.Определяема_А.Так какε₁известно, тоа_Аτ = l₁ ε₁. Далее:а_An = ,илиа_An= .Тогдаа_А = .Произведя вычисления, получим:а_А=15,8м/с'.

Ответ: v_E = 5,2м/с;v_B = 1,7м/с;с^-1; а_А = 15,8м/с².