А.Г. методичка по ТАУ (типовые звенья)(2008)

АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА «АВТОМАТИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ»

ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК И ОСНОВНЫХ СВОЙСТВ ТИПОВЫХ ЗВЕНЬЕВ С ИСПОЛЬЗОВАНИЕМ СИСТЕМЫ SIMULINK

Методические указания к лабораторным занятиям по курсу «Теория автоматического управления» для студентов специальности 220301 «Автоматизация технологических процессов и производств»

Астрахань, 2008

3

1. Цель работы

Закрепить навыки работы с пакетом прикладных программ MatLab и инструментом имитационного моделирования Simulink.

Исследовать динамические характеристики и основные свойства типовых звеньев с использованием системы Simulink.

Оценить влияние коэффициентов типовых звеньев на переходные характеристики.

2. Краткие теоретические сведения по типовым звеньям

Для расчета систем автоматического управления их разбивают на отдельные элементы, динамическими характеристиками которых являются дифференциальные уравнения не выше второго порядка. Причем различные по своей физической природе элементы могут описываться одинаковыми дифференциальными уравнениями, поэтому их относят к определенным классам, называемым типовыми звеньями.

Изображение системы в виде совокупности типовых звеньев с указанием связей между ними называется структурной схемой.

2.1. Пропорциональное звено (усилительное, безынерционное)

Пропорциональным называется звено, которое описывается уравнением

y=kx

Передаточная функция звена следующая:

Соответствующая ей структурная схема приведена на рис. 1.

Заменив в передаточной функции p на jω, получим следующие частотные характеристики:

амплитудно-фазовую:

W(jω)=k ,

вещественную частотную характеристику (рис. 2):

R(ω)=k ,

R

k

Рис. 2. ВЧХ пропорционального звена

мнимую частотную характеристику:

I(ω)=0 .

Амплитудная частотная характеристика (АЧХ) определяется соотношением:

( ) R2 ( ) I 2 ( ) R( ) k

и имеет тот же вид, что и ВЧХ. Выражение для фазовой частотной характеристики (ФЧХ):

( ) arctg[I ( )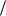 R( )] 0 .

Это означает, что амплитуда периодического входного сигнала усиливается в k - раз, а фазовый сдвиг отсутствует.

5

АФХ звена имеет вид точки на комплексной плоскости (рис. 3).

I

Рис. 3. АФХ пропорционального звена

2.2. Апериодическое звено

Апериодическим называется звено, дифференциальное уравнение которого имеет вид

Заменив в d/dt на p, перейдем к символической записи дифференциального уравнения,

(Tp+1)y = kx,

откуда определяется передаточная функция апериодического звена:

6

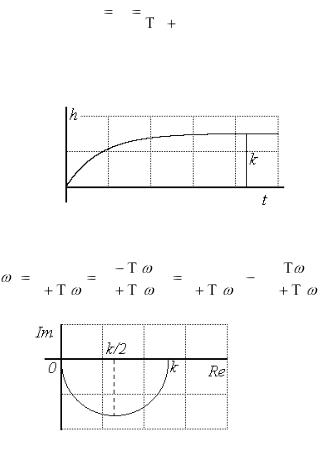
Переходная характеристика получается решением дифференциального уравнения при u=1(t) и y(0)=0 (рис. 4),

Рис. 4. Переходная характеристика апериодического звена Выражение, соответствующее АФХ апериодического звена, имеет вид:

Рис. 5. АФХ апериодического звена

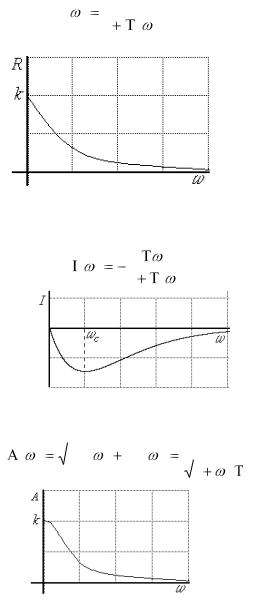
Вещественная частотная характеристика апериодического звена:

7

Рис. 6. ВЧХ апериодического звена

Мнимая частотная характеристика (рис. 7) строится по соотношению

Рис. 7. МЧХ звена

Амплитудная частотная характеристика (рис. 8) строится по выражению:

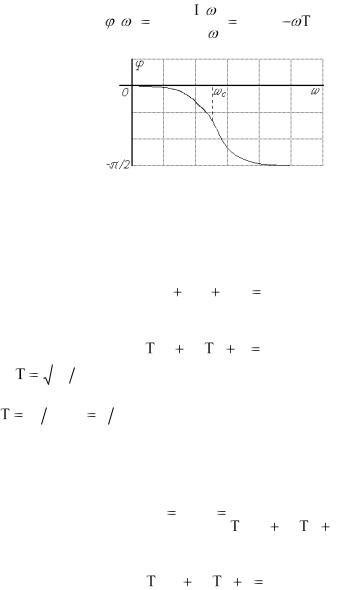
ФЧХ апериодического звена определяется соотношением:

Рис. 9. ФЧХ апериодического звена

2.3. Апериодическое звено 2-го порядка (колебательное)

Это звено, дифференциальное уравнение которого

9