
- •Краткая теория
- •Приборы, используемые в лабораторных работах
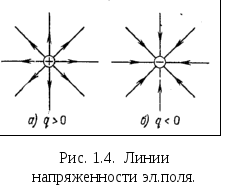
- •Общие положения
- •Подготовка и порядок работы
- •Контрольные вопросы
- •Литература
- •Определение эквипотенциальных поверхностей и линий напряженности электростатического поля
- •Краткая теория
- •Теорема Остроградского-Гаусса
- •Точечный заряд
- •Бесконечно заряженная плоскость
- •Поле 2-х бесконечных заряженных пластин
- •Поле бесконечной заряженной нити
- •Описание метода исследования и установки
- •Порядок выполнения работы
- •Задание № 1
- •Задание № 2
- •Контрольные вопросы
- •Литература
- •Измерение неизвестных емкостей при помощи баллистического гальванометра.
- •Краткая теория
- •Таким образом, электрическая емкость плоского конденсатора
- •Электрическая емкость цилиндрического конденсатора
- •Описание установки
- •Передняя панель лабораторного стенда в аудиториях № 311 и 315.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Краткая теория
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 4.
- •Краткая теория
- •Тогда окончательно получаем
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Краткая теория
- •Передняя панель лабораторного стенда в аудиториях № 311 и 315.
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Передняя панель лабораторного стенда в аудиториях № 311 и 315.
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Краткая теория
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Краткая теория
- •Описание метода эксперимента
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Краткая теория
- •Ход работы
- •Контрольные вопросы
Теорема Остроградского-Гаусса
Потоком вектора напряженности электрического поля сквозь малый участок поверхности, проведенной в поле, называется величина
dN
= E
dS
cos![]() )=
)=![]() .
(1.17)
.
(1.17)
где
![]() - вектор напряженности электрического
поля в точках малого участка поверхности
площадью dS,
- вектор напряженности электрического
поля в точках малого участка поверхности
площадью dS,
![]() -
единичный вектор, нормальный к площадке
dS,
а вектор
-
единичный вектор, нормальный к площадке
dS,
а вектор
![]() .
.
dN = EndS = EdS . (1.18)
Поток напряженности N сквозь любую поверхность S равен алгебраической сумме потоков напряженности сквозь все малые участки этой поверхности:
![]() .
(1.19)
.
(1.19)
При
этом все векторы
![]() нормалей к малым площадкам dS
нужно направлять в одну и ту же сторону
относительно поверхности S.
нормалей к малым площадкам dS
нужно направлять в одну и ту же сторону
относительно поверхности S.
Рассмотрим электростатическое поле системы точечных зарядов q1, q2, ..., qn. Согласно принципу суперпозиции полей:
![]() ,
(1.20)
,
(1.20)
т.е. искомый поток N равен алгебраической сумме потоков через ту же замкнутую поверхность S напряженности полей каждого из зарядов системы. Поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической сумме электрических зарядов, охватываемых этой поверхностью, к электрической постоянной 0.
![]() .
(1.21)
.
(1.21)
Рассмотрим несколько примеров использования теоремы Остроградского-Гаусса.
Точечный заряд
Рассмотрим
точечный заряд, помещенный в центре
сферы радиусом R.
По теореме Остроградского-Гаусса dN
= EdS
=
![]() ,
учитывая, что Sсферы
= 4R2,
то
,
учитывая, что Sсферы
= 4R2,
то
![]() .
(1.22)
.
(1.22)
Бесконечно заряженная плоскость
Р ассмотрим
равномерно заряженную бесконечную
плоскость с постоянной поверхностной
плотностью заряда:
ассмотрим
равномерно заряженную бесконечную
плоскость с постоянной поверхностной
плотностью заряда:
![]() -
это заряд, распределенный по площади
S.
-
это заряд, распределенный по площади
S.
Вектор электрического поля будет направлен нормально от плоскости, если >0.
Для определения модуля вектора напряженности, создаваемого пластиной, применим теорему Гаусса к замкнутой цилиндрической поверхности (рис. 1.5). Ось цилиндра перпендикулярна заряженной плоскости, и последняя делит высоту цилиндра пополам. Оба основания параллельны заряженной плоскости и имеют одинаковую площадь S.
Поток вектора напряженности через цилиндрическую поверхность равен:
![]() (1.23)
(1.23)
На боковой поверхности вектор E параллелен поверхности и cosα = 0. На торцах цилиндра вектор E перпендикулярен поверхности и cosα = 1, а величина E одинакова на обоих основаниях; следовательно,
![]()
![]() (1.24)
(1.24)
Проведенная цилиндрическая поверхность вырезает из плоскости такую же площадку S c полным зарядом:
![]() (1.25)
(1.25)
Подставляя (1.24) и (1.25) в левую и правую части (1.21) получаем:
откуда
![]() (1.26)
(1.26)
Поле 2-х бесконечных заряженных пластин


Рис.1 .5.
Поле двух пластин.
Из
чертежа (рис.1.5.) видно, что в областях I
и III
из-за наложения полей общая Е
= 0, и только в средней ЕII
=
2EI.
Учитывая, что ЕI
одной плоскости равна:
![]() ,
тогда для 2ух плоскостей получаем:
,
тогда для 2ух плоскостей получаем:
![]() .
(1.27)
.
(1.27)
