Решение:

Рис. 1.6 а к примеру решения задач 1.3

В задаче рассматриваются два тела, связанные нитью и совершающие поступательное движение. На тело массы действуют сила тяжестисила нормальной реакциинаклонной плоскости, сила натяжениянити и сила трения. На телодействуют только сила тяжестии сила натяжениянити (рис.1.6). В условиях равновесия ускорения первого и второго тела равны нулю, а сила трения является силой трения покоя, и ее направление противоположно направлению возможного движения тела. Применяя второй закон Ньютона для первого и второго тела, получаем систему уравнений:

(1)

Bследствие невесомости нити и блока . Выбрав оси координат (рис.1.6а, 1.6 б), запишем для каждого тела уравнение движения в проекциях на эти оси. Тело начнет опускаться (рис. 1.6а) при условии:

(2)

При совместном решении системы (2) можно получить

(3)

С учетом того, что выражение (3) можно записать в виде:

(4)

Тело начнет подниматься при условии (рис.1.6 б): (5)

При совместном решении системы (5) можно получить:

(6)

Тело будет находиться в покое при условии:

Ответ: 1) 2)

3) .

1.4. Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузы с массами и(). Кабина начинает подниматься с ускорением. Пренебрегая массами блока и нити, а также трением, найти:

1. ускорение груза относительно шахты лифта и относительно кабины;

2. силу, с которой блок действует на потолок кабины.

Дано: Найти:

1.

2. .

.

Решение:

Грузы идвижутся относительно кабины лифта и участвуют в движении лифта с ускорением. Если нить не растяжима, то ускорения грузов относительно кабины одинаковы по модулю и противоположны по направлению:

=

.

Относительно шахты лифта ускорения грузов:

Для проекций на ось OY эти уравнения можно переписать в виде:

= (1)

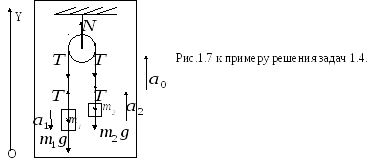
Каждый из грузов движется под действием силы тяжести и силы натяжения нити. Параллельность сил, действующих на каждый из грузов, позволяет записать уравнения движения сразу в скалярной форме для проекций на ось OY:

(2)

Решая систему (1) относительно , можно получить:

. (3)

Подставляя (3) в систему уравнений (2), получим выражение для ускорения груза относительно шахты лифта:

.

Подставляя уравнения системы (1) в систему уравнений (2)

(4)

и решая систему уравнений (4), можно получить выражение для ускорения груза относительно кабины лифта:

.

Сила давления блока на ось гдесила реакции оси, действующая на блок и направленная вертикально вверх. Кроме этой силы на блок действуют силы натяжения нити, направленные вниз. Уравнение второго закона Ньютона для блока имеет вид:

где ускорение блока относительно Земли,его масса. Еслито независимо от ускорения блока

Для проекций на ось OY данное уравнение можно переписать в виде:

Уравнения (4) образуют систему с двумя неизвестными Т и а. Умножая первое уравнение этой системы на m₂, а второе на m₁ и складывая их почленно, можно получить:

.

Искомая сила давления блока на потолок кабины

, тогда

.

Ответ: 1. , ;

2. .