Информатика / Matem

Математика

Авторы:

Игорь Иосифович Клебанов Алексей Васильевич Дудин Елена Владимировна Коробейникова

Введение Математика как наука о моделях Логика

Основные математические структуры Элементы теории вероятностей математической статистики Случайные величины Генеральная совокупность. Выборка Задачи

Введение

Настоящее пособие представляет собой конспект лекций, читавшихся одним из авторов (И.И.Клебановым) студентам исторического факультета ЧГПУ. Курс рассчитан на 14 часов лекций и 10 часов практических занятий, после чего студенты приступают к изучению основ информатики. Пособие охватывает весь материал курса «Математика для гуманитариев», предусмотренный государственным стандартом, за исключением темы «Математические модели», поскольку содержание последней определяется узкой специализацией слушателей (поэтому вместо конспекта соответствующей лекции мы приводим примерный план). Остальной же материал «инвариантен» при переходе от одной гуманитарной специальности к другой, и нуждается лишь в обогащении специфическим примерами.

Пособие не рассчитано на самостоятельное изучение предмета, а должно, по замыслу авторов, стать «затравкой» для активного общения преподавателя-математика со студентом-гуманитарием. Если гуманитарий в процессе работы перестанет безоговорочно соглашаться с первым «определением» математики, вынесенным в эпиграф, осознаем второе и задумается над третьим – задачу курса можно считать выполненной.

Математика как наука о моделях

Примерный план:

1.Задачи Дидоны (изопериметрическая задача). 2.Задача Эйлера о Кенигсбергских мостах (графы).

3.Модели роста народонаселения Земли (модели Мальтуса и Капицы).

Логика

Излагаются элементарные сведения о языке математической логики.

Для передачи информации люди используют жесты, слова, символы. В различных науках используются специфические наборы слов и символов. Например, любой язык состоит из букв, которые складываются в слова. Для каждой науки характерен свой набор понятий и символов.

Математика – не исключение. Язык математики – математическая логика.

Логика возникла почти одновременно с философией в конце VII в.- начале VI в. до н.э. в Греции. Несколько позднее логические системы появились в Китае и Индии. Основатели

логики – Зенон и Сократ. Они первыми поставили вопрос о том, как мы мыслим и говорим. Первый философ, предложивший развитую схему логики, был Аристотель. Он создал логику, которая просуществовала до XVIII в. После свой вклад в развитие логики внес Гегель. С XVII в. происходит процесс математизации логики, осуществляемый Паскалем, Лейбницем, и в XIX веке - Булем. Они ввели в логику математический аппарат. Теперь логика – самостоятельный раздел математики.

Что же такое логика?

Логикой (logos – слово, учение) называют учение о закономерностях, которым подчинен наш язык и мышление. Это философское определение логики.

Азбукой языка логики являются символы, которыми математики любят заменять слова. Эти символы называются кванторами.

Примеры кванторов.

Основными объектами, которые изучает математическая логика, являются высказывания.

В математике под высказыванием подразумевается любое предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Например, предложение «В настоящее время на улице идет дождь» может быть как истинным, так и ложным. Заметим, что конкретное содержание высказывания не имеет существенной важности. Важно только истинно оно или ложно.

Пусть p и q являются предложениями, (высказываниями).

Они могут принимать только два значения. Если каждое из высказываний перевести в вопросительную форму, то на эти вопросы можно ответить «Да» или «Нет» в зависимости от истинности или ложности высказывания.

Договоримся об обозначениях: 1 – истина.

0 – ложь.

(Обратите внимание на аналогию с двоичной системой исчисления).

Над предложениями можно осуществлять логические операции. Вернее, не над самими предложениями, а над их значениями. Результаты операций удобно представлять в табличном виде. Такие таблицы называются таблицами истинности. Рассмотрим основные логические операции и соответствующие им таблицы истинности.

1. Отрицание. Обозначается как p. Читается как «не P»

р р

1 0

0 1

2. Двойное отрицание

Примем эту операцию без таблицы, которая очевидна.

3. Конъюнкция p q. Соответствует логическому И. Конъюнкция считается истинной, когда истинны оба высказывания (как p так и q).

Конъюнкция похожа на операцию умножения. Её иногда называют логическим умножением.

Аналогия: 1*0=0*1=0; 1*1=1; 0*0=0.

Свойства конъюнкции:

p q = q p - свойство коммутативности;

(p q) r = p (q r) – свойство ассоциативности; p p = p – свойство идемпотентности.

4. Дизъюнкция p q. Соответствует логическому ИЛИ. Дизъюнкция считается истинной, если верно хотя бы одно из утверждений.

Свойства дизъюнкции напоминают свойства операции сложения. Свойства дизъюнкции:

∙p q = q p

∙p q r = q r p

∙p p = p

Аналогия: 1+0=0+1=1; 1+1+0=1+0+1=0+1+1; 0+0=0.

Таким образом, дизъюнкция обладает теми же свойствами коммутативности, ассоциативности и идемпотентности, что и конъюнкция.

Пример:

Доказать равенство p (q r) = (p q) (p r) Доказательство:

1 способ. По аналогии с умножением раскрываем скобки.

p(q + r) = pq + pr (доказано)

2 способ. Проведем доказательство с помощью таблицы истинности. Для этого разобьем сложное высказывание на несколько простых, найдем их значение при всех возможных значениях переменных, тогда после подстановки значений простых высказываний в левую и правую части равенства, мы должны получить одинаковые последовательности нулей и единиц (в таблице выделены жирным шрифтом).

Математик и логик Де Морган установил два закона, названных его именем.

1закон: p q = р q (неверно ни p, ни q)

2закон: p q = p q (неверно либо p, либо q)

5. Импликация p→q (следование: если… то). Таблица для импликации.

Построим импликацию на основе предложений: Р – государство является правовым

Q – закон не имеет обратной силы

Если государство является правовым, то закон не имеет обратной силы (истина). Если государство является правовым, то закон имеет обратную силу (ложь).

6. Двойная импликация (эквиваленция) p q (тогда и только тогда, когда). Если p, то q, и если q, то p.

Таблица двойной импликации.

Пример двойной n импликации:

Государство является правовым тогда и только тогда, когда закон не имеет обратной силы.

Введем далее понятия абсолютной истины и абсолютной лжи. I – абсолютная истина.

L – абсолютная ложь. I≡1 L≡0

Тогда очевидны следующие утверждения:

Приведем основные тождества, важные в математической логике:

1.импликация – это дизъюнкция, т.е. p→q = p q

2.двойная импликация – это конъюнкция, т.е. p q = p q

Применим, наконец, законы математической логики к решению задачи «детективного характера».

На судебном процессе рассматривается сложное дело. Три обвиняемых по этому делу: Иванов, Петров, Сидоров. Их обвиняют в ограблении банка. Суду необходимо установит истину. Каждый дает следующие показания:

Иванов: банк не грабил, но видел, что грабитель уехал на синих Жигулях. Петров: банк не грабил, но видел, что грабитель уехал на черной Волге. Сидоров: банк не грабил, но видел, что грабитель уехал на Запорожце.

Каждый из обвиняемых хотя бы один раз солгал, а один раз сказал правду. Требуется определить, на какой машине (и какого цвета) уехал грабитель.

Для установления истины сформулируем предложения: P – машина синего цвета.

Q– Жигули.

R– машина черного цвета.

T– Запорожец.

S– Волга.

Поскольку хотя бы одно из утверждений истинно, истинны следующие дизъюнкции:

P Q = I R S = I P T = I

Значит,

(P Q) (R S) (P T) = I

Запишем иначе:

(P + Q ) (R + S) (P + T) = (PR + QR + PS + QS) (P + T) = PR P + QR P + PS P + QS P + PRT + QRT + PST + QST

Вычеркиваем все ложные утверждения, т.е.

PRP + QRP + PS P + QS P + PRT + QRT + PST + QST

Дизъюнкция верна, если хотя бы одно из слагаемых верно, отсюда следует, что грабитель уехал на черных Жигулях.

Основные математические структуры

Излагаются элементарные сведения о множествах, числах, координатах и функциях. На прошлой лекции мы познакомились с языком математики – логикой. Следующие две лекции посвятим рассмотрению основных элементов, из которых могут быть построены сколь угодно сложные математические объекты. Эти элементы называются основными математическими структурами. Таковыми являются множества, числа и функции.

I. Множество – наиболее фундаментальная математическая структура. Любое понятие в

математике можно описать с помощью теории множеств.

Что же такое множество? Множество – это набор (совокупность) предметов любой природы, например, множество студентов в аудитории.

Множества в математике обозначаются заглавными буквами латинского алфавита, например, множество А, множество В и т.д. Чтобы определить (задать) множество, нужно определиться с его элементами.

Множество можно задать способом перечисления. Например:

В– множество цветов радуги.

В= {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}.

Еще один способ задания множеств. Задание с помощью характеристического свойства. Это свойство характеризует все элементы, входящие в данное множество. Этот способ задания множеств является в математике оптимальным, так как существуют множества с бесконечным числом элементов. Например, нельзя перечислить все натуральные числа, большие нуля.

А = {а | свойство} Например: А = {а | студенты}

Введем обозначение принадлежности элемента множеству: аÎА обозначает, что элемент а принадлежит множеству А;

аÏA обозначает, что элемент а не принадлежит множеству А.

Иногда одно множество является частью другого (А – первое множество, В – второе

множество), тогда запись такого условия будет выглядеть следующим образом: ВÌA. Над множествами можно производить различные операции.

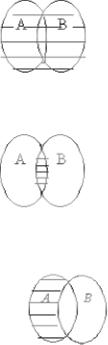
1. Операция объединения АÈВ Объединением множеств "А" и "В" является множество элементов, которые входят либо в множество "А", либо в множество "В".

2. Операция пересечения множеств АÇВ.

Пересечением множеств А и В является множество элементов, которые входят как в множество А, так и в множество В.

3. Разность множеств А \ В.

Разностью множеств А и В является множество элементов А, которые не входят в множество В.

4. Равенство множеств А = В.

Если множество А полностью входит в множество В, и при этом В полностью входит в А, то множества А и В равны.

Приведем простейшие примеры операций с множествами Возьмем множества:

А= {1,2,3,4,5,6} В = {0,3,5,7} АÈВ = { 0,1,2,3,4,5,6,7 }

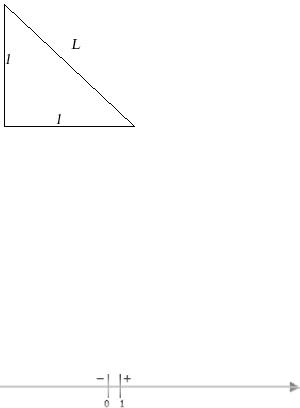
АÇВ= { 3,5 } А \ В = {1,2,4,6 }

II

Следующим по степени фундаментальности является понятие числа.

Числа начинаются с натурального ряда 1,2,3…или, говоря иначе, с модели счета предметов.

Множество натуральных чисел в математике обозначается N.

Операции, которые можно произвести с натуральными числами, не выходя за рамки множества:

1.сложение;

2.умножение.

Рассмотрим операцию вычитания Х+5=1

Нельзя решить такое уравнение на множестве натуральных чисел. Возникают элементы, не входящие в него. Надо ввести дополнительные понятия: множество отрицательных натуральных чисел и множество, состоящее из нуля.

NU–NU0=Z - множество целых чисел.

Попытаемся теперь решить в целых числах уравнение 2*X=3.

Такое уравнение нельзя решить на множестве целых чисел. Таким образом, множество чисел нуждается в расширении. Чтобы построить такое, расширение вводим понятие дробных (рациональных) чисел Q. Эти числа можно отобразить в виде несократимых дробей вида m/n, где m и n – целые числа. Но и это еще не предел. Со времен древних математиков существовали на первый взгляд неразрешимые задачи. Одним из первых их пытался решить их Пифагор. Перед ним в частности, стояла следующая задача: можно ли найти такое рациональное число, квадрат которого равен 2?

Рис. 1 Эту задачу одним из первых решил Евклид. Он рассуждал методом от противного.

Пусть ЕСТЬ такое рациональное число. Тогда L2= 2 и L = m>/n, где m, n Î Z. Тогда m2 = 2n2

Построим цепь импликаций

m2= 2n2 Þn2 – четное число Þ m – четное число Þm = 2р, где р Î Z.

4р2= 2n2 или n2 = 2р2 n2 – четное число Þ n - четное число Þ дробь m/n сократима (противоречие условию) Þ нет такого рационального числа.

Таким образом, приходится признать, что существует множество чисел, не являющихся рациональными. Вводим понятие иррационального числа. Если множества рациональных и иррациональных чисел объединить, то получим множество вещественных чисел.

В математике вещественные числа можно представить в виде точек числовой оси, хорошо известной из курса элементарной математики.

Какую бы точку мы ни отметили, ей всегда будет сопоставляться вещественное число. Таким образом, мы окончательно построили понятие вещественного числа.

Пример: Шкала летоисчисления. (Нуль – рождество Христово, масштаб, например, 1000 лет)

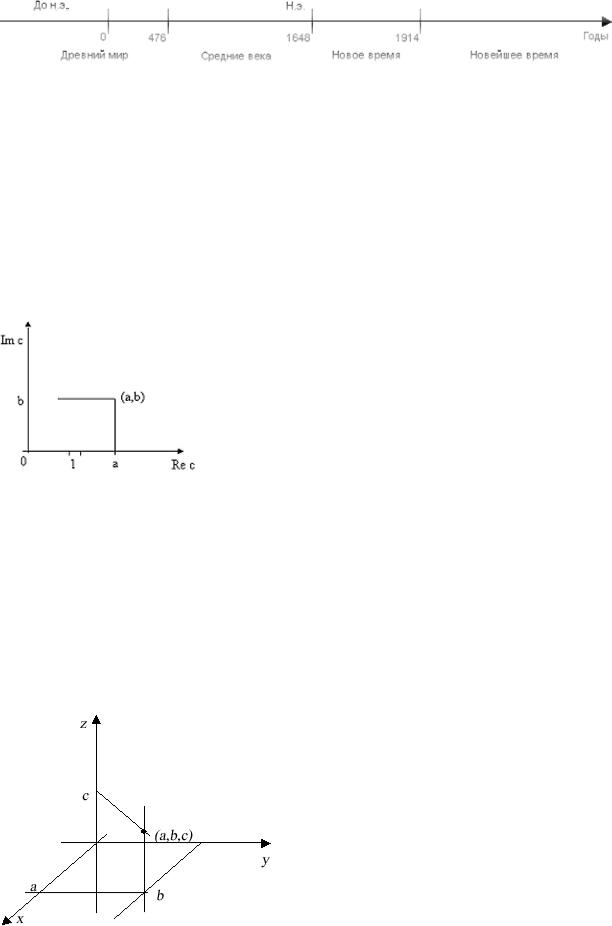
Шкала летоисчисления обладает замечательным свойством. Линия времени показывает, что прогресс идет все быстрее и быстрее. Она коррелирует с моделью Капицы [3], который предложил модель роста населения Земли. Время сжимается так же стремительно, как растет человечество.

Но есть еще числа, которые невозможно отобразить на числовой прямой. Попробуем решить уравнение X2 = -1

Ясно, что такого вещественного числа нет. Введем, однако, число "i", которое по определению, будучи возведенным в квадрат, равно –1. Число i называется мнимой единицей. Тогда, с помощью мнимой единицы можно создать более сложную «конструкцию», называемую комплексным числом.

Пусть даны два вещественных числа а и b. Тогда число c = a + ib назовем комплексным, а

– его вещественной частью, b – его мнимой частью, а число c = a – ib – комплексно сопряженным.

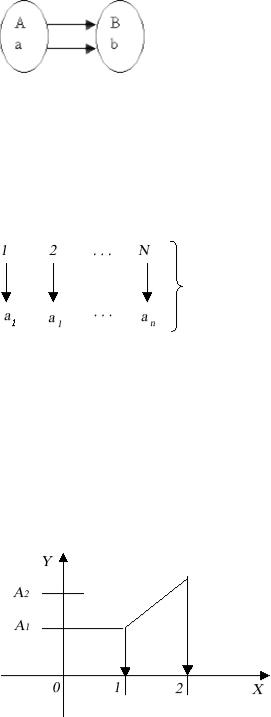
Изобразим комплексные числа, для чего введем систему координат.

Здесь 'Im' означает мнимую часть (imaginarus), а 'Re' – вещественную часть (real). После того, как мы сказали о множествах различных чисел, поговорим о том, как выглядит их запись. В основе привычной нам записи чисел лежит десятичная система исчисления.

Например:

123 = 3 * 100 + 2 * 101 + 1 * 102 – десятичная система.

Но могут быть системы с другим основанием. Двоичная – неплохой вариант.

10011 – в двоичной системе, 10011 = 1 * 20 + 1 * 21 + 0 * 22 + 0 * 23 + 1 * 24=1 + 2 + 0 + 0 + 8 = 11 – в десятичной.

Существуют наглядные способы отображения чисел и отношений между ними. Декарт очень любил ходить в театр и всегда бывал недоволен, когда в зале возникала путаница с местами для зрителей. Он решил эту проблему, создав способ нумерации мест. Развив этот метод и применив его к математическим объектам, получаем метод координат.

C помощью координатного метода удобно изображать любые математические конструкции, например, те же множества. (В качестве примера применения координатного метода для решения практических задач полезно рассмотреть задачу о

диете [1]).

III

Следующей фундаментальной математической структурой является отображение множеств. Если между элементами двух множеств устанавливается соответствие, то говорят, что задано отображение множеств.

Пример – Петровский «Табель о рангах», в котором каждому военному чину ставился в соответствие гражданский (капитан – титулярный советник, фельдмаршал – канцлер).

Если каждому элементу множества А ставится в соответствие не более 1 элемента множества В, то о таких соответствиях говорят, как о функциях.

Если Х – элемент множества А, Y – элемент множества В, то это соответствие записывается в виде:

Y = f (X).

Первое соответствие такого рода – числовая последовательность.

Пусть имеем множество натуральных чисел N: 1,2,3… Поставим каждому натуральному числу в соответствие какое-нибудь вещественное число и запишем это следующим образом:

Тогда говорят, что задана числовая последовательность. Три способа задания числовой последовательности.

1 табличный

2 графический

3 аналитический (с помощью формул)

аn = n2

(В качестве примеров «интересных» последовательностей полезно рассмотреть арифметическую и геометрическую прогрессии и ряд Фибоначчи [1]). Возьмем теперь множество действительных чисел и каждому числу поставим в

соответствие другое действительное число. Тогда, если первый элемент Х, второй элемент Y, то говорят, что задана функция одного вещественного переменного.

Y = f (X)

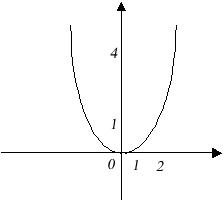
Впервые такое обозначение ввел немецкий математик Лейбниц. Рассмотрим функцию Y= X2

Если это отображение изобразить на плоскости , то получим линию, называемую параболой (соответствующая таблица приводится рядом).

Рис 3.

Функции играют роль «кирпичиков» для такой области математики как математический анализ.

Определенные виды функций называются элементарными. Вот только некоторые из них:

1.степенная функция Y= Xn, где n – любое вещественное число.

2.показательная функция Y= ax , где а > 0, а ¹ 1.

3.логарифмическая функция Y = logaX, где а > 0, а ¹1.

4.тригонометрические функции Sin X, Cos X, tg X, ctg X и обратные к ним arcsin X, arccos X, arctg X, arcctg X.

Элементы теории вероятностей и математической статистики

Массовые случайные события. Статистическое и классическое определение вероятности. Сложение и умножение вероятностей. Формулы полной вероятности и Байеса.

1. Массовые случайные события Вероятность относится к числу понятий, которыми мы охотно пользуемся в повседневной

жизни, совсем не задумываясь об этом. Например, даже наша речь носит отпечаток стихийно-вероятностного подхода к окружающей нас действительности:

-Мы пойдем завтра на хоккей?

-Вероятно…

-Ты уверен, что Богданова изберут в комиссию?

-Маловероятно…

-Вы слышали, что Филатов развелся?

-Невероятно!!!

Уже в этих коротких репликах «вероятно, маловероятно, невероятно» имеется попытка оценить возможность появления того или иного события, т. е. попытка дать количественную (числовую) оценку этой возможности. Идея выражать числами степень возможности появления тех или иных событий возникла после того, как люди наблюдали множество примеров, в которых проявлялось удивительное свойство устойчивости явлений, т. е. способность повторяться довольно часто. Многие из этих примеров стали классическими.