Построение пусковой диаграммы

Построение пусковой диаграммы и определение пусковых сопротивлений выполняют аналитическим или графическим методами. Аналитический метод применяется при высокой линейности механических характеристик. Графический метод в большей степени учитывает нелинейность механической характеристики и отличается от аналитического тем, что после расчета максимального момента (М₁) и момента переключения (М₂) правильная пусковая диаграмма строится путем последовательных приближений с корректировкой значений М₂.

1. Определяю значение момента М₁ через найденное ранее значение М_Н. Для этого используется заданная в табл.2 кратность пускового момента М₁/М_Н =2

М₁ = 2*175,99= 351,98

Рассчитываю величину момента переключения М₂:

, где , аm – число пусковых ступеней, равное в данной работе для всех вариантов 3 (m=3).

α=

М₂ = 351,98/2,12=166,03 Н·м

Строю пусковую диаграмму привода в координатах естественной механической характеристики.

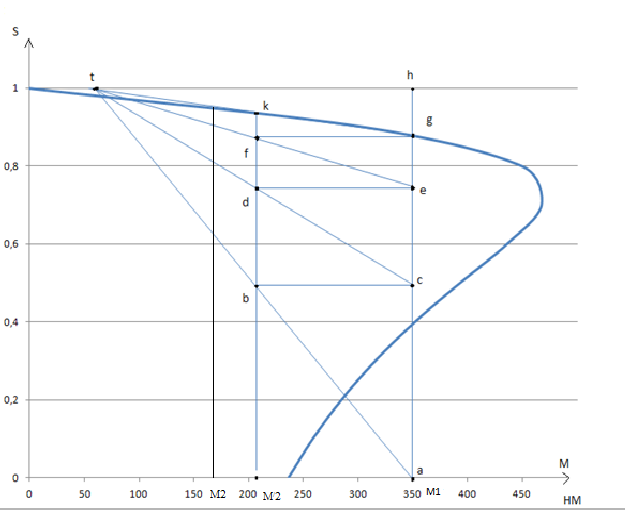
Рис.3 Графический расчет пусковой диаграммы.

Расчет пусковых параметров электропривода.

К расчетным пусковым параметрам электропривода в первую очередь относятся значения сопротивлений пусковых реостатов и время пуска.

Значения сопротивлений отдельных секций пусковых реостатов определяется с помощью построенной пусковой диаграммы, лучи которой разбили вертикальные линии моментов М₁, М₂ на ряд отрезков (ac, ce, eg), соотношение длин которых пропорционально соотношению сопротивлений секций.

Определяю значения сопротивлений секций по следующим формулам:

R_G1 = ac  m_R;

R_G2 = ce  m_R;

R_G3 = eg  m_R,

где m_R – масштаб сопротивлений равный: m_R = R_P / gh.

R_P - активное сопротивление одной фазы обмотки ротора, определяемое по формуле:

,

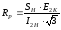где Е_2К – напряжение между кольцами двигателя, а I_2H- ток ротора при полученном значении ПВ. Оба параметра определяются из технических данных электродвигателей серии MTF (табл.3).

Значения ac, ce, eg, gh беру из пусковой диграммы.

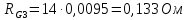
Для определения времени пуска необходимо выполнить приведение момента инерции механизма к валу двигателя по формуле:

= 1,25 + 1,75 * (42 / 99,43)² = 1,56 кгс*м

момент инерции двигателя J_ДВ = (CD)²/4 = 1,25; (CD)²/4 – маховый момент двигателя

момент инерции механизма J_МЕХ = 1,75;

Номинальная скорость вращения механизма w_МЕХ =42 рад/c;

Номинальная скорость вращения двигателя

w_ДВ = n_ДВ/30 = 3,14*950/30=99,43 рад/с.

Рассчитываю время пуска двигателя из неподвижного состояния до рабочей скорости (w_ДВ), считая, что двигатель разгоняется под действием среднеарифметического момента.

Вместо момента М₂ использую уточненный момент М^/₂.

М_СР = (М₁ + М^/₂)/2=(351,98+210)/2=280,99

а момент статического сопротивления механизма

М_С  Р_С1 / w_ДВ.=3750/99,43=37,7

Тогда время пуска двигателя равно:

t_П = J  w_ДВ /( М_СР - М_С)=1,5699,43/(280,99-37,7)=0,64

Задание №2.

«Исследование стабильности регулирования скорости электропривода в замкнутых и разомкнутых системах»

Первая цифра варианта	5
Тип двигателя ПБСТ	43
Коэффициент усиления системы Кс = КусКув	500
Вторая цифра варианта	9
Скорость вращения холостого хода wo. рад/с	220

Тип двигателя ПБСТ	43
Номинальная мощность Рн, кВт	3,8
Номинальная скорость вращения соН , рад/с	230
Номинальное напряжение UН, В	220
Номинальный ток якоря 1Н, А	19,5
Номинальный момент МН, Нм	16,5
Номинальный КПД, η	88,3
Коэффициент двигателя С, Вс	0,9
Сопротивление якорной обмотки нагретого двигателя RЯ, Ом	0,63

Суммарное сопротивление якорной цепи принимаю равным

R_ЯЦ =2,1R_Я=2,1*0,63= 1,323

где R_Я - сопротивление якорной обмотки нагретого двигателя, выбираемое из табл.

Задающее напряжение в замкнутой системе вычисляю из соотношения

U_ЗЗС = w₀ · (1+K_C/C) / (K_C/C)= 220 · (1+0,04500/0,9) / (500/0,9)=8,36

где Кс = Кус · Кув - коэффициент усиления системы электропривода;

С=КФ - коэффициент двигателя;

 - коэффициент обратной связи по скорости = 0,04 Вс.

Задающее напряжение в замкнутой системе вычисляется из соотношения

U_ЗРС = w₀ · C / K_C = 220 · 0,9 / 500=0,396

которое вытекает из соотношения для замкнутой системы при =0.

Уравнение механической характеристики в разомкнутой системе определяется известным уравнением

W_РС=U_ЗРСК_С/С - МR_ЯЦ/С²= 220 – М1,323/0,9²=220-1,63М

где U_ЗРСК_С/С= w₀=220.

Механическую характеристику w=f(M) для разомкнутой системы можно построить по двум точкам, т.к. она представляет собой прямую линию. Координаты первой точки w= w₀, М=0, координаты второй w=w(M_Н), М=М_Н.

Уравнение механической характеристики в замкнутой системе определяется уравнением

W_РС=U_ЗЗСК_С/(С+K_C ) - МR_ЯЦ/С(С+K_C )=

=220 – М1,323/(0,9(0,9+0,04500 ))=220-0,07М

где U_ЗЗСК_С/(С+K_C )=w₀=220 .

Механическую характеристику w=f(M) для замкнутой системы также можно построить по двум точкам, т.к. она представляет собой прямую линию. Координаты первой точки w= w₀, М=0, координаты второй w=w(M_Н), М=М_Н.

Для разомкнутой системы:

M	0	16,5
w	220	193,1

Для замкнутой системы :

M	0	16,5
w	220	218,8

По результатам расчета механических характеристик для разомкнутой и замкнутой систем строю механические характеристики в соответствии с рис. 4.

Рис.4.Механические характеристики для разомкнутой (2) и замкнутой(1) систем регулирования.

Используя данные полученных механических характеристик рассчитываю параметры статизма в разомкнутой и замкнутой системах управления.

w_Р / w₀ = 26,95/220=0,122;

w_З / w₀ =1,16/220=0,0053.