
- •Электростатика, постоянный электрический ток, электромагнитные явления
- •Оглавление
- •1. Электростатика.
- •2. Постоянный электрический ток.
- •3. Электромагнитные явления.
- •Пояснительная записка к тестовым заданиям
- •2. Постоянный электрический ток
- •3. Электромагнитные явления
- •Заключение
- •Библиографический список
- •Приложения
- •Основные уравнения электростатики в вакууме
- •Постоянный электрический ток
- •Квантовая теория электропроводности металлов
- •Зонная теория электропроводности твердых тел
- •Электромагнитные явления
- •Явление электромагнитной индукции. Самоиндукция
- •Дифференциальная форма закона электромагнитной индукции:
- •Энергия магнитного поля. Объемная плотность энергии магнитного поля
- •Напряженность электрического поля (поля Холла)
- •1) Для изотропных проводников, в частности для поликристаллов
- •2) Для анизотропных веществ
- •Период и частота собственных электромагнитных колебаний:
- •Условие возникновения апериодических колебаний:
- •Добротность колебательного контура
- •Цепи квазистационарного переменного тока
- •Основные физические постоянные (округленные значения)
- •Некоторые астрономические величины
- •Относительные атомные массы (округленные значения) Аr и порядковые номера z некоторых элементов
- •Свойства некоторых твердых тел
- •Некоторые параметры электроизолирующих материалов
- •Некоторые свойства сегнетоэлектрических кристаллов
- •Пьезоэлектрические модули некоторых кристаллов
- •Удельное сопротивление и температурный коэффициент сопротивления металлов
- •Сплавы с высоким омическим сопротивлением
- •Электрохимические эквиваленты
- •Температура перехода некоторых металлов, сплавов и соединений в сверхпроводящее состояние
- •Абсолютные нормальные потенциалы некоторых металлов
- •Подвижность электронов в металлах ( 10-4 м2/(с×в)
- •Допустимые токи (а) в изолированных проводах при продолжительной работе
- •Электрическое поле в атмосфере Земли
- •Свойства важнейших полупроводников
- •Приложение 3
- •Правильные ответы на тестовые задания
- •Электростатика, постоянный электрический ток,
- •Электромагнитные явления
- •Электростатика, постоянный электрический ток, электромагнитные явления
3. Электромагнитные явления
1. Магнитостатика – раздел теории электромагнитного поля, в котором изучаются свойства:
а) стационарных полей постоянных электрических токов или поля постоянных магнитов а также движение заряженных частиц в стационарном магнитном поле;
б) магнитного поля (полей постоянных электрических токов или поля постоянных магнитов) а также движение заряженных частиц в магнитном поле;
в) стационарных магнитных полей (полей постоянных электрических токов или поля постоянных магнитов) а также движение заряженных частиц в стационарном магнитном поле.
2. Теорема эквивалентности поля магнитных зарядов и поля постоянных электрических токов (теорема Ампера) утверждает:
а) магнитное поле предельно тонкого плоского магнита ("магнитного листка"), образованного из одинаково ориентированных элементарных магнитиков, тождественно полю замкнутого (кругового) линейного тока, текущего по контуру этого магнита;
б) магнитное поле замкнутого (кругового) линейного тока, текущего по контуру предельно тонкого плоского магнита ("магнитного листка"), образованного из одинаково ориентированных элементарных магнитиков, тождественно магнитному полю предельно плоского магнита ("магнитного листка");
в) магнитное поле любого плоского магнита, образованного из одинаково ориентированных элементарных магнитиков, тождественно полю замкнутого (кругового) линейного тока, текущего по контуру этого магнита.
3. Макротоки это:
а) упорядоченное движение электрических зарядов;
б) упорядоченное движение только электронов в объеме проводника;
в) упорядоченное движение электрических зарядов в объеме проводника.
4. Микротоки обусловлены:
а) наличием в атомах вещества электрических зарядов, вращающихся вокруг ядер с большой скоростью (1015 с-1), при этом движение каждого электрона эквивалентно замкнутому контуру с током;
б) наличием в атомах вещества электронов, вращающихся вокруг ядер с большой скоростью (1015 с-1), при этом движение каждого электрона эквивалентно замкнутому контуру с током;
в) наличием в атомах вещества протонов, вращающихся вокруг ядер с большой скоростью (1015 с-1), при этом движение каждого электрона эквивалентно замкнутому контуру с током.
5. Орбитальный магнитный момент микротока вещества определяется соотношением:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ,
,
где I – величина эквивалентного тока (микротока); S – площадь орбиты электрона.
6. Пробный ток (пробный контур) это ток:
а) существующий в любом замкнутом контуре малых размеров (круговой ток). Положение этого контура в пространстве определяется с помощью положительной нормали, связанной с током в контуре правилом правого винта;
б) существующий в плоском замкнутом контуре малых размеров (круговой ток). Положение этого контура в пространстве определяется с помощью положительной нормали, связанной с током в контуре правилом правого винта;
в) существующий в плоском замкнутом контуре малых размеров (круговой ток). Положение этого контура в пространстве определяется с помощью положительной нормали, связанной с током в контуре правилом векторного умножения.
7. Магнитный момент пробного тока (пробного контура) это:
а) векторная физическая величина, характеризующая свойства пробного контура, численно равная произведению величины тока в контуре на площадь, охватываемая контуром;
б) физическая величина, характеризующая свойства пробного контура, численно равная произведению величины тока в контуре на площадь, охватываемая контуром;
в) векторная физическая величина, не характеризующая свойства пробного контура, численно равная произведению величины тока в контуре на площадь, охватываемая контуром.
8. Вращающий момент, действующий на пробный контур:
а) скалярная физическая величина пропорциональная его магнитному моменту, синусу угла между направлением положительной нормали и направлением магнитного поля в данном месте пространства;
б) векторная физическая величина пропорциональная его магнитному моменту, синусу угла между направлением положительной нормали и направлением магнитного поля в данном месте пространства;
в) векторная физическая величина равная произведению его магнитного момента на синусу угла между направлением положительной нормали и направлением магнитного поля в данном месте пространства и площади, охватываемой контуром.
9. Численное значение вращающего момента, действующего на пробный контур определяется соотношением:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() .
.
10. Связь вращающего момента, действующего на пробный контур в магнитном поле с индукцией и напряженностью магнитного поля устанавливается соотношением:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ,
,
где pm – магнитный момент пробного контура; B – вектор индукции магнитного поля; Н – вектор напряженности магнитного поля; – угол между векторами pmи B; – магнитная проницаемость среды; 0 – магнитная постоянная.
11. Индукция магнитного поля это:
а) векторная физическая величина, численно равная вращающему моменту, действующему на пробный контур, помещенный перпендикулярно к направлению магнитного поля в данную точку, магнитный момент которого равен единице;
б) скалярная физическая величина, численно равная вращающему моменту, действующему на пробный контур, помещенный перпендикулярно к направлению магнитного поля в данную точку, магнитный момент которого равен единице;
в) векторная физическая величина, численно равная вращающему моменту, действующему на пробный контур, помещенный перпендикулярно к направлению магнитного поля в данную точку.
12. Индукция магнитного поля характеризует:
а) силовое воздействие магнитного поля макро – и микротоков только на движущиеся электроны;
б) силовое воздействие магнитного поля макро – и микротоков на движущиеся электрические заряды;
в) силовое воздействие магнитного поля макро – и микротоков только на движущиеся протоны;
г) силовое воздействие магнитного поля макро – и микротоков на только на движущиеся ионы.
13. При прочих равных условиях и одном и том же токе в проводнике величина индукции магнитного поля в различных средах:
а) остаётся величиной постоянной;
б) различна;
в) зависит от свойств среды.
14. Индукция магнитного поля характеристика магнитных полей порождаемых:
а) только макротоками;
б) только микротоками;
в) макротоками и микротоками.
15. Напряженность магнитного поля характеристика магнитных полей порождаемых:
а) только макротоками;
б) только микротоками;
в) макротоками и микротоками.
16. При прочих равных условиях и одном и том же токе в проводнике величина напряженности магнитного поля в различных средах:
а) не зависит от свойств среды;
б) различна;
в) зависит от свойств среды.
17. Вектор намагниченности это характеристика магнитных полей порождаемых:
а) макротоками вещества;
б) микротоками вещества;
в) макротоками и микротоками вещества.
18. В вакууме вектор намагниченности:
а) равен нулю;
б) больше нуля;
в) меньше нуля.
19. В отсутствие внешнего магнитного поля в магнетике вектор намагниченности:
а) равен нулю;
б) больше нуля;
в) меньше нуля.
20. В веществах во внешнем магнитном поле (кроме так называемых ферромагнетиков и не слишком сильных полях) связь между вектором напряженности магнитного поля и вектором намагниченности можно записать так:
а)
 ;
;
б)
![]() ;
;
в)
 ;
;
г)
![]() ,
,
где m – магнитная восприимчивость вещества (характеризует его магнитные свойства); – магнитная проницаемость среды; 0 – магнитная постоянная.
21. Связь между векторами B, H и J можно записать так:
а)
 ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ,
где
– относительная магнитная проницаемость
среды; m
– магнитная восприимчивость вещества;
0
– магнитная постоянная.
,
где
– относительная магнитная проницаемость
среды; m
– магнитная восприимчивость вещества;
0
– магнитная постоянная.
2 2.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А равен:
2.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А равен:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
2 3.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А равен:
3.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А равен:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
2 4.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А направлен:
4.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А направлен:
а) влево; б) вниз; в) вверх; г) вправо; д) среди приведенных ответов правильного ответа нет.
2 5.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А направлен:
5.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=I2,
то вектор В
индукции результирующего поля в точке
А направлен:
а) влево; б) вниз; в) вверх; г) вправо; д) среди приведенных ответов правильного ответа нет.
26.
М агнитное
поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А равен:
агнитное
поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А равен:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
2 7.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А равен:
7.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А равен:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
2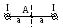 8.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А направлен:
8.
Магнитное поле создано двумя параллельными
длинными проводниками с токамиI1
и I2,
расположенными перпендикулярно плоскости
чертежа. Если I1=2I2,
то вектор В
индукции результирующего поля в точке
А направлен:
а) влево; б) вниз; в) вверх; г) вправо.

29. Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа. Если I1=2I2, то вектор В индукции результирующего поля в точке А направлен:
а) влево; б) вниз; в) вверх; г) вправо.
3 0.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
0.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
а) а; б) с; в) b; г) d; д) среди приведенных ответов правильного ответа нет.
3 1.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
1.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
а) а; б) с; в) b; г) d; д) среди приведенных ответов правильного ответа нет.
3 2.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
2.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
а) а; б) с; в) b; г) d.
3 3.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
3.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Индукция В
результирующего магнитного поля равна
нулю в некоторой точке интервала:
а) а; б) с; в) b; г) d.
3 4.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
4.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
3 5.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
5.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
3 6.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
6.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
3 7.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
7.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
3 8.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
8.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
3 9.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
9.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
4 0.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
0.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.

41. На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем I1=2I2. Вектор индукции В результирующего магнитного поля в точке А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.

42. На рисунке изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем I1=2I2. Вектор индукции В результирующего магнитного поля в точке А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
4 3.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
3.
На рисунке изображены сечения двух
параллельных прямолинейных длинных
проводников с противоположно направленными
токами, причемI1=2I2.
Вектор индукции В
результирующего магнитного поля в точке
А направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
44. Индукция магнитного поля созданного объёмным элементом тока (закон Био-Савара-Лапласа) в точке, находящейся на расстоянии |r|=r определяется соотношением:
а)
 ;
б)
;
б) ;
в)
;
в)![]()
 ;
;
г)
 .
.
45. Индукция магнитного поля созданного линейным элементом тока (закон Био-Савара-Лапласа) в точке, находящейся на расстоянии |r|=r определяется соотношением:
а)
 ;
б)
;
б) ;
;
в)
![]()
 ;
г)
;
г) .
.
46. Результирующая индукция магнитного поля для замкнутых постоянных токов в точке, находящейся на расстоянии |r|=r определяется соотношением:
а)
![]()
 ;
б)
;
б) ;
;
в)
 ;
г)
;
г) .
.
47. Индукция магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r от оси проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
;
в)
 ;
г)
;
г) ,
,
где I – сила тока в проводнике; r – расстояние от элемента проводника dℓ до рассматриваемой точки поля; 1, 2 – углы между направлением тока в проводнике и направлением на рассматриваемую точку поля.
48. Напряженность магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r от оси проводника, определяется по формуле:
а)
 ;
;
б)
 ;
;
в)
 ;
;
г)
 ,
где I – сила тока в проводнике; r –
расстояние от элемента проводника dℓ
до рассматриваемой точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
,
где I – сила тока в проводнике; r –
расстояние от элемента проводника dℓ
до рассматриваемой точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
49. При симметричном расположении точки М относительно концов проводника индукция магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r от оси проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
;
в)
 ;
г)
;
г) ,
где I – сила тока в проводнике; r –
расстояние от проводника до рассматриваемой
точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
,
где I – сила тока в проводнике; r –
расстояние от проводника до рассматриваемой
точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
50. При симметричном расположении точки М относительно концов проводника напряженность магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r от оси проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 ,
где I – сила тока в проводнике; r –
расстояние от проводника до рассматриваемой
точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
,
где I – сила тока в проводнике; r –
расстояние от проводника до рассматриваемой
точки поля;1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
51. Индукция магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r0 от оси проводника, определяется по формуле:
а)
 ;
б)
;
б)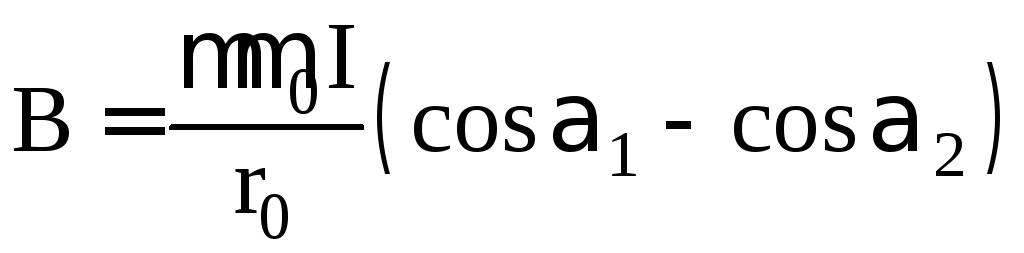 ;
;
в)
 ;
г)
;
г) ,
где I – сила тока в проводнике; r0
– расстояние от проводника до
рассматриваемой точки поля; 1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
,
где I – сила тока в проводнике; r0
– расстояние от проводника до
рассматриваемой точки поля; 1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
52. Напряженность магнитного поля прямолинейного бесконечно длинного проводника с током в точке М, находящейся на расстоянии r0 от оси проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 ,
где I – сила тока в проводнике; r0
– расстояние от проводника до
рассматриваемой точки поля; 1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
,
где I – сила тока в проводнике; r0
– расстояние от проводника до
рассматриваемой точки поля; 1,
2
– углы между направлением тока в
проводнике и направлением на рассматриваемую
точку поля.
5 3.
В общем случае графически изменение
напряженности магнитного поля проводника
от расстояния до его оси можно представить
так, как показано на рисунке:
3.
В общем случае графически изменение
напряженности магнитного поля проводника
от расстояния до его оси можно представить
так, как показано на рисунке:
а) 1; б) 2; в) 3.
54. На оси кругового проводника радиусом R, в котором существует ток I, индукция магнитного поля в точке М, находящейся на расстоянии r0 от центра проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
;
в)
 ;
г)
;
г) ,
где R – радиус кругового проводника; r0
– расстояние от центра проводника до
рассматриваемой точки поля на оси
кругового проводника.
,
где R – радиус кругового проводника; r0
– расстояние от центра проводника до
рассматриваемой точки поля на оси
кругового проводника.
55. На оси кругового проводника радиусом R, в котором существует ток I, индукция магнитного поля в точке М, находящейся на расстоянии r0 от центра проводника, определяется по формуле:
а)
 ;
б)
;
б) ;
;
в)
 ;
г)
;
г) ,
где R – радиус кругового проводника; r0
– расстояние от центра проводника до
рассматриваемой точки поля на оси
кругового проводника.
,
где R – радиус кругового проводника; r0
– расстояние от центра проводника до
рассматриваемой точки поля на оси
кругового проводника.
56. В центре кругового проводника радиусом R, в котором существует ток I, индукция магнитного поля, определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)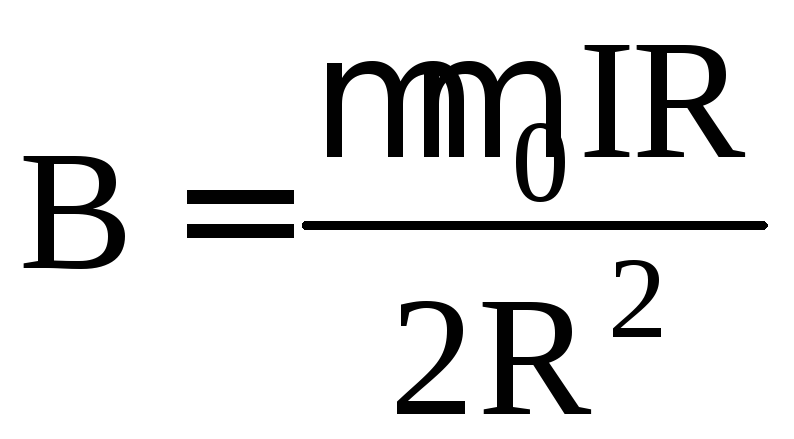 ,
где R – радиус кругового проводника.
,
где R – радиус кругового проводника.
57. В центре кругового проводника радиусом R, в котором существует ток I, напряженность магнитного поля, определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) ,
где R – радиус кругового проводника.
,
где R – радиус кругового проводника.
5 8.
Внутри соленоида в произвольной точке
А (соленоид – катушка цилиндрической
формы из проволоки, витки которой
намотаны в одном направлении и прилегают
плотно друг к другу) индукция магнитного
поля определяется по формуле:
8.
Внутри соленоида в произвольной точке
А (соленоид – катушка цилиндрической
формы из проволоки, витки которой
намотаны в одном направлении и прилегают
плотно друг к другу) индукция магнитного
поля определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 ,
где
– длина соленоида; N
– число витков; R
– радиус соленоида; 1,
2
– углы, под которыми видны концы соленоида
из рассматриваемой точки А внутри его.
,
где
– длина соленоида; N
– число витков; R
– радиус соленоида; 1,
2
– углы, под которыми видны концы соленоида
из рассматриваемой точки А внутри его.
5 9.
Внутри соленоида в произвольной точке
А (соленоид – катушка цилиндрической
формы из проволоки, витки которой
намотаны в одном направлении и прилегают
плотно друг к другу) напряженность
магнитного поля определяется по формуле:
9.
Внутри соленоида в произвольной точке
А (соленоид – катушка цилиндрической
формы из проволоки, витки которой
намотаны в одном направлении и прилегают
плотно друг к другу) напряженность
магнитного поля определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 ,
где
– длина соленоида; N
– число витков; R
– радиус соленоида; 1,
2
– углы, под которыми видны концы соленоида
из рассматриваемой точки А внутри его.
,
где
– длина соленоида; N
– число витков; R
– радиус соленоида; 1,
2
– углы, под которыми видны концы соленоида
из рассматриваемой точки А внутри его.
60. Внутри бесконечно длинного соленоида индукция и напряжённость магнитного поля определяются по формулам:
а)
![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() ;
в)
;
в)![]() ,
,![]() ;
;
г)
![]() ,
,![]() ,
гдеN
– число витков соленоида; n=N/
– число витков на единице длины соленоида;
I – величина тока в соленоиде.
,
гдеN
– число витков соленоида; n=N/
– число витков на единице длины соленоида;
I – величина тока в соленоиде.
61. Внутри соленоида конечной длины индукция и напряженность магнитного поля определяется по формулам:
а)
![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() ;
;
в)
![]() ,
,![]() ;
г)
;
г)![]() ,
,![]() ,
гдеN
– число витков соленоида; n=N/
– число витков на единице длины соленоида;
I – величина тока в соленоиде.
,
гдеN
– число витков соленоида; n=N/
– число витков на единице длины соленоида;
I – величина тока в соленоиде.
62. Внутри тороида на его оси (тороид – соленоид, свитый в кольцо) индукция и напряженность магнитного поля определяется по формулам:
а)
![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() ;
;
в)
![]() ,
,![]() ;
г)
;
г)![]() ,
,![]() ,
гдеN
– число витков.
,
гдеN
– число витков.
6 3.
Внутри тороида на произвольном расстоянииr
от его центра индукция и напряженность
магнитного поля определяется по формулам:
3.
Внутри тороида на произвольном расстоянииr
от его центра индукция и напряженность
магнитного поля определяется по формулам:
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ;
;
в)
![]() ,
,![]() ;
;
г)
![]() ,
,![]() ,
гдеN
– число витков тороида; R
– радиус тороида по средней линии; r –
радиус тороидального кольца; I – сила
тока; n – число витков на единицу длины
тороида.
,
гдеN
– число витков тороида; R
– радиус тороида по средней линии; r –
радиус тороидального кольца; I – сила
тока; n – число витков на единицу длины
тороида.
64. Закон полного тока (теорема о циркуляции индукции магнитного поля) в интегральной форме: утверждает:
а) циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению 0 на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока должны быть связаны между собой правилом левого винта);
б) циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению 0 на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока не играют ни какой роли);
в) циркуляция вектора индукции магнитного поля по замкнутому контуру L равна произведению 0 на алгебраическую сумму токов, охватываемых контуром (направление обхода контура и направление тока должны быть связаны между собой правилом правого винта).
65. В интегральной форме закон полного тока можно записать:
а)
 ;
б)
;
б) ;
;
в)
 ,
гдеn
– число проводников с токами, охватываемых
контуром L
произвольной формы.
,
гдеn
– число проводников с токами, охватываемых
контуром L
произвольной формы.
66. Условие вихревого характера (не потенциальности) магнитного поля определяется соотношением:
а)
 ;
б)
;
б) ;
в)
;
в)![]() .
.
67. Поток магнитной индукции (магнитный поток) через площадку dS это:
а) физическая величина, численно равная произведению проекции B на направление положительной нормали n к площадке dS и величины этой площадки;
б) физическая величина, численно равная произведению вектора B на направление положительной нормали n к площадке dS и величины этой площадки;
в) физическая величина, численно равная произведению вектора B на величину площадки dS.
68. Элементарный магнитный поток (поток магнитной индукции) через площадку dS определяется соотношением:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ,
где
– угол между векторами B
и
n;
Bn=Bcos
– проекция вектора B
на направление положительной нормали
к площадке dS.
,
где
– угол между векторами B
и
n;
Bn=Bcos
– проекция вектора B
на направление положительной нормали
к площадке dS.
69. Полный поток магнитной индукции через некоторую поверхность S определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
70. Математически теорема Остроградского-Гаусса для магнитных полей можно записать так:
а)
 ;
б)
;
б) ;
;
в)
 .
.
71. На рисунке представлена магнитная цепь, состоящая из стального сердечника с воздушным (вакуумным) зазором. Индукция магнитного поля B в такой магнитной цепи, определяется соотношением:
а )
) ;
;
б)
 ;
;
в)
 ,
где ℓc
ℓВ
– соответственно длина стального и
воздушного участков цепи; с,
В
– их относительные магнитные
проницаемости;0
– магнитная постоянная; I
– ток в обмотке цепи; N
– число витков обмотки.
,
где ℓc
ℓВ
– соответственно длина стального и
воздушного участков цепи; с,
В
– их относительные магнитные
проницаемости;0
– магнитная постоянная; I
– ток в обмотке цепи; N
– число витков обмотки.
72. Математически закон Ома для магнитных цепей можно записать так:
а)
 ;
б)
;
б) ;
;
в)
 ,
где IN – магнитодвижущая сила;
,
где IN – магнитодвижущая сила; – магнитное сопротивление цепи
сердечника;
– магнитное сопротивление цепи
сердечника; – магнитное сопротивление цепи воздушного
зазора.
– магнитное сопротивление цепи воздушного
зазора.
73. Первый закон (первое правило) Кирхгофа для магнитных цепей утверждает: «Алгебраическая сумма магнитных потоков в участках цепи сходящихся в узле»:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
74. На рисунке представлена схема магнитной цепи, состоящая из трех независимых замкнутых магнитных контуров. Для такой замкнутой цепи в точке А справедливо соотношение:
а )
)![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
7 5.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров. Для такой
замкнутой цепи в точке В справедливо
соотношение:
5.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров. Для такой
замкнутой цепи в точке В справедливо
соотношение:
а)
![]() ;
;
б)
![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() .
.
7 6.
На рисунке представлена схема магнитной
цепи. Для такой замкнутой цепи в точке
А справедливо соотношение:
6.
На рисунке представлена схема магнитной
цепи. Для такой замкнутой цепи в точке
А справедливо соотношение:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
77. Второй закон (второе правило) Кирхгофа для магнитных цепей утверждает: «В любом замкнутом магнитном контуре, произвольно выбранном в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитное сопротивление соответствующих участков цепи»:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
7 8.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров – (абдеа;
бвгдб;
авгеа).
Для замкнутого контура абдеа
справедливо соотношение:
8.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров – (абдеа;
бвгдб;
авгеа).
Для замкнутого контура абдеа
справедливо соотношение:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
7 9.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров – (абдеа;
бвгдб;
авгеа).
Для замкнутого контура авгеа
справедливо соотношение:
9.
На рисунке представлена схема магнитной
цепи, состоящая из трех независимых
замкнутых магнитных контуров – (абдеа;
бвгдб;
авгеа).
Для замкнутого контура авгеа
справедливо соотношение:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.

80. На рисунке представлена схема магнитной цепи, состоящая из трех независимых замкнутых магнитных контуров – (абдеа; бвгдб; авгеа). Для замкнутого контура бвгдб справедливо соотношение:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
81. На каждый элемент проводника dℓ с током в магнитном поле действует сила (сила Ампера):
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() .
.
82. На проводник конечной длины ℓ с током в магнитном поле действует сила (сила Ампера):
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 .
.
83. Величина силы, действующей со стороны однородного магнитного поля на прямолинейный проводник с током:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
84. Величина силы, действующей со стороны неоднородного магнитного поля на произвольный проводник с током:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
85. Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен:
а) равна произведению силы тока на величину магнитного потока через поверхность проводника;
б) равна произведению силы тока на величину магнитного потока через поверхность, замкнутого проводника;
в) равна произведению силы тока на величину магнитного потока через поверхность, которую не описывает проводник при своем движении;
г) равна произведению силы тока на величину магнитного потока через поверхность, которую описывает проводник при своем движении.
86. Работа по перемещению проводника с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен и проводник прямолинейный определяется по формуле:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ,
где I – величина тока в контуре;Ф
– изменение магнитного потока.
,
где I – величина тока в контуре;Ф
– изменение магнитного потока.
87. Работа, совершаемая силами Ампера при перемещении в магнитном поле контура, ток в котором постоянен, равна
а) произведению силы тока на изменение магнитного потока через любую поверхность;
б) произведению силы тока на изменение магнитного потока через поверхность, ограниченную контуром;
в) произведению силы тока на магнитный поток через поверхность, ограниченную контуром.
88. Работа по перемещению контура с током в магнитном поле (работа, совершаемая силами Ампера), ток в котором постоянен определяется по формуле:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ,
где I – величина тока в контуре;dФ
– изменение магнитного потока.
,
где I – величина тока в контуре;dФ
– изменение магнитного потока.

89.
На рисунке изображено некоторое вещество,
помещенное во внешнее магнитное поле
напряженностью
![]() .
В этом случае вектор намагничивания
.
В этом случае вектор намагничивания![]() будет направлен по направлению:
будет направлен по направлению:
а) 1; б) 2; в) 3; г) 4.
9 0.
На рисунке изображено некоторое вещество,
помещенное во внешнее магнитное поле
напряженностью
0.
На рисунке изображено некоторое вещество,
помещенное во внешнее магнитное поле
напряженностью![]() .
После намагничивания оказалось, что
вектор намагничивания
.
После намагничивания оказалось, что
вектор намагничивания![]() направлен по направлению противоположному
вектору напряженности внешнего магнитного
поля
направлен по направлению противоположному
вектору напряженности внешнего магнитного
поля![]() .
Данное вещество является:
.
Данное вещество является:
а) парамагнетиком; б) диамагнетиком; в) ферромагнетиком;
г) ферримагнетиком.
9 1.
На рисунке изображено некоторое вещество,
помещенное во внешнее магнитное поле
напряженностью
1.
На рисунке изображено некоторое вещество,
помещенное во внешнее магнитное поле
напряженностью![]() .
После намагничивания оказалось, что
вектор намагничивания
.
После намагничивания оказалось, что
вектор намагничивания![]() направлен по направлению вектора
напряженности внешнего магнитного поля
направлен по направлению вектора
напряженности внешнего магнитного поля![]() .
Данное вещество является:
.
Данное вещество является:
а) парамагнетиком; б) диамагнетиком; в) ферромагнетиком;
г) ферримагнетиком.
92. Диамагнетизм это свойство веществ, обусловленное действием внешнего магнитного поля на:
а) электронные орбиты атомов и молекул;
б) частицы (атомы, молекулы, ионы, атомные ядра), которые обладают собственным магнитным моментом;
в) на векторы намагниченности доменов.
93. Парамагнетизм это свойство веществ, обусловленное действием внешнего магнитного поля на:
а) электронные орбиты атомов и молекул;
б) частицы (атомы, молекулы, ионы, атомные ядра), которые обладают собственным магнитным моментом;
в) на векторы намагниченности доменов.
94. Ферромагнетизм это свойство веществ, обусловленное действием внешнего магнитного поля на:
а) электронные орбиты атомов и молекул;
б) частицы (атомы, молекулы, ионы, атомные ядра), которые обладают собственным магнитным моментом;
в) на векторы намагниченности доменов.
95. В диамагнетиках намагничивание состоит в:
а) возникновении микроскопических индукционных токов, создающих намагниченность, направленную против внешнего магнитного поля;
б) из ориентации хаотически колеблющихся магнитных моментов атомов или ионов в направлении внешнего магнитного поля;
в) переориентации векторов намагниченности доменов в направлении внешнего магнитного поля.
96. В парамагнетиках намагничивание состоит в:
а) возникновении микроскопических индукционных токов, создающих намагниченность, направленную против внешнего магнитного поля;
б) из ориентации хаотически колеблющихся магнитных моментов атомов или ионов в направлении внешнего магнитного поля;
в) переориентации векторов намагниченности доменов в направлении внешнего магнитного поля.
97. В ферромагнетиках намагничивание состоит в:
а) возникновении микроскопических индукционных токов, создающих намагниченность, направленную против внешнего магнитного поля;
б) из ориентации хаотически колеблющихся магнитных моментов атомов или ионов в направлении внешнего магнитного поля;
в) переориентации векторов намагниченности доменов в направлении внешнего магнитного поля.

98. На рисунке представлено возможное движение электрона вокруг ядра. Указаны направления эквивалентного тока, электрического момента и его скорости. Вектор механического момента импульса (количества движения) в этом случае будет направлен по направлению….
а) 1; б) 2; в) 3; г) 4.
9 9.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокI:
9.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокI:
а) намагничивание на этом участке достигается за счет обратимого упругого смещения доменных границ;
б) магнитная проницаемость на этом участке изменяется по линейному закону;
в) характеризуется постоянной магнитной проницаемостью .
1 00.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокII:
00.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокII:
а) намагничивание на этом участке достигается за счет обратимого упругого смещения доменных границ;
б) намагничивание на этом участке происходит с необратимостью смещения доменных границ (закон Рэлея);
в) на этом участке при намагничивании происходят необратимые процессы.
1 01.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокIII:
01.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокIII:
а) характеризуется высоким значением магнитной проницаемости (восприимчивости).
б) на этом участке намагниченность меняется большими скачками;
в) характеризуется высоким значением магнитной проницаемости (восприимчивости). На этом участке намагниченность меняется большими скачками.
1 02.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокIY:
02.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокIY:
а) характеризуется постепенным уменьшением магнитной проницаемости ;
б) на участке намагничивание осуществляется за счет вращения векторов спонтанной намагниченности в направлении внешнего магнитного поля;
в) работа по повороту векторов спонтанной намагниченности затрачивается против энергии кристаллографической анизотропии.
1 03.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокY:
03.
На рисунке представлена кривая
намагничивания, которую можно разбить
на пять участков. УчастокY:
а) характеризуется незначительным намагничиванием, связанным с дополнительной ориентацией спиновых магнитных моментов в направлении поля;
б) на этом участке процессы смещения и вращения магнитных моментов закончены;
в) характеризуется незначительным намагничиванием, связанным с дополнительной ориентацией спиновых магнитных моментов в направлении поля. На этом участке процессы смещения и вращения магнитных моментов закончены.
1 04.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости диамагнетиков
от напряженности внешнего магнитного
поля?:
04.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости диамагнетиков
от напряженности внешнего магнитного
поля?:
а) 1; б) 2; в) 3; г) 4.
1 05.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости парамагнетиков
от напряженности внешнего магнитного
поля?:
05.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости парамагнетиков
от напряженности внешнего магнитного
поля?:
а) 1; б) 2; в) 3; г) 4.
1 06.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости ферромагнетиков
от напряженности внешнего магнитного
поля?:
06.
На рисунке представлены зависимости
относительной магнитной проницаемости
некоторых сред от напряженности внешнего
магнитного поля. Какая из зависимостей
соответствует изменению относительной
магнитной проницаемости ферромагнетиков
от напряженности внешнего магнитного
поля?:
а) 1; б) 2; в) 3; г) 4.
107. На рисунке представлено возможное движение электрона вокруг ядра. Указаны направления эквивалентного тока, момента импульса (количества движения) и его скорости. Вектор электрического момента в этом случае будет направлен по направлению:
а )
1; б) 2; в) 3; г) 4.
)
1; б) 2; в) 3; г) 4.
108. Точка Кюри это температура, при которой намагниченность насыщения Js равна:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
109. Домены ферромагнитные это области:
а) самопроизвольной однородной намагниченности в ферромагнетике в отсутствие внешнего магнитного поля, намагниченные до насыщения части объема ферромагнетика, на которые он разбивается ниже критической температуры (точки Кюри);
б) самопроизвольной однородной намагниченности в ферромагнетике в отсутствие внешнего магнитного поля, векторы намагниченности в которых ориентированы таким образом, что результирующая намагниченность ферромагнитного образца в целом, как правило, равна нулю;
в) химически однородной среды, отличающиеся электрическими, магнитными или упругими свойствами, либо упорядоченностью в расположении частиц.
1 10.
На рисунке изображена зависимость
относительной деформации образца из
сплава железо-никель от напряженности
внешнего магнитного поля (магнитострикция).
Продольной магнитострикции соответствует
кривая:
10.
На рисунке изображена зависимость
относительной деформации образца из
сплава железо-никель от напряженности
внешнего магнитного поля (магнитострикция).
Продольной магнитострикции соответствует
кривая:
а) I; б) II; в) среди приведенных ответов правильного ответа нет.
1 11.
На рисунке изображена зависимость
относительной деформации образца из
сплава железо-никель от напряженности
внешнего магнитного поля (магнитострикция).
Продольной магнитострикции соответствует
кривая:
11.
На рисунке изображена зависимость
относительной деформации образца из
сплава железо-никель от напряженности
внешнего магнитного поля (магнитострикция).
Продольной магнитострикции соответствует
кривая:
а) I; б) II; в) среди приведенных ответов правильного ответа нет.
112. Коэрцитивная сила Hc это величина:
а) напряженности магнитного поля, в котором ферромагнетик, первоначально намагниченный до насыщения, дополнительно намагничивается;
б) напряженности магнитного поля, в котором ферромагнетик, первоначально намагниченный до насыщения, не изменяет свои магнитные свойства;
в) напряженности магнитного поля, в котором ферромагнетик, первоначально намагниченный до насыщения, размагничивается.
113. Остаточная индукция Bs это величина:
а) характеризующая магнитное поле в ферромагнетике во внешнем магнитном поле;
б) характеризующая магнитное поле в веществе даже в отсутствие внешнего магнитного поля;
в) характеризующая магнитное поле в ферромагнетике даже в отсутствие внешнего магнитного поля.
114. Кривые намагничивания это:
а) графики, отображающие зависимость намагниченности J или магнитной индукции B от напряженности внешнего магнитного поля H;
б) таблицы, отображающие зависимость намагниченности J или магнитной индукции B от напряженности внешнего магнитного поля H;
в) формулы, отображающие зависимость намагниченности J или магнитной индукции B от напряженности внешнего магнитного поля H.
115. Остаточная намагниченность Jr – намагниченность Jr, которую имеет ферромагнетик при напряженности внешнего магнитного поля:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
116. Антиферромагнетизм это магнитоупорядоченное состояние вещества, характеризующееся тем, что магнитные моменты соседних частиц вещества (атомных носителей магнетизма) ориентированы навстречу друг другу (антипараллельно), и поэтому намагниченность тела в целом в отсутствие магнитного поля:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
117. Магнитострикция это:
а) изменение формы ферромагнетиков и ферримагнетиков при их намагничивании;
б) изменение размеров ферромагнетиков и ферримагнетиков при их намагничивании;
в) изменение формы и размеров ферромагнетиков и ферримагнетиков при их намагничивании.
118. Магнитоупругий эффект (эффект Виллари) это:
а) обратное по отношению к магнитострикции явление;
б) изменение намагниченности ферромагнитного образца при деформации;
в) изменение намагниченности ферромагнитного образца при нагревании.
119. Магнитное охлаждение – метод получения температур путем адиабатического размагничивания парамагнитных веществ:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
120. Магнетокалорический эффект это:
а) изменение температуры магнетика при адиабатическом изменении напряженности магнитного поля H, в котором он находится;
б) изменение формы магнетика при адиабатическом изменении напряженности магнитного поля H, в котором он находится;
в) изменение линейных размеров магнетика при адиабатическом изменении напряженности магнитного поля H, в котором он находится.
121. На границе раздела двух магнетиков (сред) нормальные составляющие вектора B и тангенциальные составляющие вектора H непрерывны. При этом:
а)
 ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
 .
.
122. Электромагнитная индукция это явление:
а) возникновения электродвижущей силы (распределенной ЭДС электромагнитной индукции) в незамкнутом проводнике, находящемся в переменном магнитном поле;
б) возникновения электродвижущей силы (распределенной ЭДС электромагнитной индукции) в проводящем контуре, находящемся в постоянном магнитном поле;
в) возникновения электродвижущей силы (распределенной ЭДС электромагнитной индукции) в проводящем контуре, находящемся в переменном магнитном поле;
г) возникновения электродвижущей силы (распределенной ЭДС электромагнитной индукции) в проводящем контуре движущимся в постоянном магнитном поле.
123. Основной закон электромагнитной индукции (закон Фарадея): «При пересечении потока магнитной индукции отрезком проводника в нем возникает ЭДС электромагнитной индукции, которая прямо пропорциональна скорости изменения величины магнитного потока». При этом:
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) ,
где
,
где![]() – скорость изменения магнитного потока;
– скорость изменения магнитного потока;![]() – скорость изменения индукции магнитного
поля.
– скорость изменения индукции магнитного
поля.
124. Основной закон электромагнитной индукции (закон Фарадея): «При пересечении потока магнитной индукции отрезком проводника в нем возникает ЭДС электромагнитной индукции, которая прямо пропорциональна скорости изменения величины магнитного потока». При этом:
а) в любом проводнике возникает индукционный ток;
б) в замкнутом проводнике возникает индукционный ток;
в) в замкнутом проводнике индукционный ток не возникает;
г) в прямолинейном не замкнутом проводнике индукционный ток не возникает.
125. Правило Ленца утверждает, что индукционный ток всегда направлен так, что создаваемый им поток магнитной индукции через поверхность, ограниченную контуром:
а) стремится препятствовать причине, его порождающей;
б) никакого влияния не оказывает на причину его порождающую;
в) оказывает действие на причину его порождающую.
126. Самоиндукция это явление возникновения ЭДС электромагнитной индукции в каком-либо контуре вследствие изменения магнитного потока:
а) создаваемого электрическим током другого контура с током;
б) создаваемого электрическим током этого же контура;
в) создаваемого электрическим током проводника, расположенного вблизи этого контура.
127. Величина ЭДС самоиндукции определяется по формуле:
а)
;
 ;
б)
;
б) ;
;
в)
 .
.
128.
Формула
 определяет:
определяет:
а) ЭДС самоиндукции, возникающую в бесконечно длинном соленоиде;
б) ЭДС самоиндукции, возникающую в бесконечно длинном проводнике;
в) ЭДС самоиндукции, возникающую в любом проводнике.
129.
Формула
 определяет:
определяет:
а) ЭДС самоиндукции, возникающую в любом проводнике;
б) ЭДС самоиндукции, возникающую в бесконечно длинном проводнике;
в) ЭДС самоиндукции, возникающую в бесконечно длинном соленоиде.
130. Индуктивность (коэффициент индуктивности) это:
а) физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при любой скорости изменения тока в нем;
б) физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при скорости изменения тока в нем равной 1 А/с;
в) физическая величина, характеризующая магнитные свойства электрической цепи, зависящая от размеров и формы электрической цепи, а также от магнитной проницаемости окружающей среды.
131. На рисунке представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре не возникает на интервале:
а )E;
б) C;
в) A;
г) B;
д) D.
)E;
б) C;
в) A;
г) B;
д) D.
132.
Формула
 определяет:
определяет:
а) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L при включении источника ЭДС;
б) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L при выключении источника ЭДС;
в) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L и ёмкости С при включении источника ЭДС.
133.
Формула
 определяет:
определяет:
а) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L при включении источника ЭДС;
б) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L при выключении источника ЭДС;
в) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L и ёмкости С при включении источника ЭДС.
134.
Формула
 отображает закон Ома при наличии в цепи:
отображает закон Ома при наличии в цепи:
а) индуктивности L, ёмкости С и сопротивления R;
б) индуктивности L и ёмкости С;
в) ёмкости С и сопротивления R.
135.
Формула
 определяет:
определяет:
а) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и ёмкости С при включении источника ЭДС;
б) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и ёмкости С при выключении источника ЭДС;
в) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L и ёмкости С при включении источника ЭДС.
136.
Формула
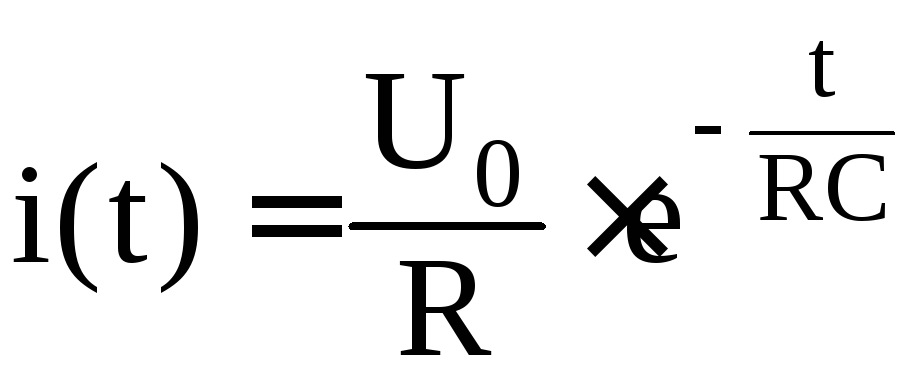 определяет:
определяет:
а) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и ёмкости С при включении источника ЭДС;
б) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и ёмкости С при выключении источника ЭДС;
в) изменение тока в цепи, состоящей из соединенных последовательно сопротивления R и индуктивности L и ёмкости С при включении источника ЭДС.
137.
Выражение W=![]() определяет энергию магнитного поля,
создаваемого током I в контуре,:
определяет энергию магнитного поля,
создаваемого током I в контуре,:
а) индуктивность которого L; б) длина которого L; в) площадь которого L.
138. Объемная плотность энергии магнитного поля это физическая величина, которая показывает, какой энергией обладает магнитное поле,:
а) занимающее некоторый объем пространства; б) занимающее всё пространство; в) занимающее единицу объема пространства;
139.
Формула
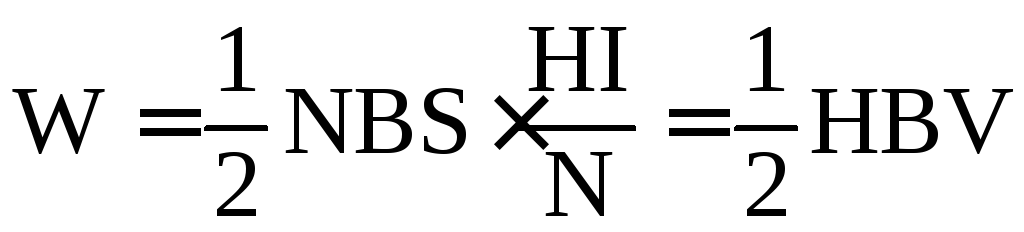 определяет:
определяет:
а) объёмную плотность энергии магнитного поля; б) плотность энергии магнитного поля; в) энергию магнитного поля соленоида.
140. Энергию магнитного поля соленоида можно определить по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
141. Объёмную плотность энергии магнитного поля длинного соленоида можно определить по формуле:
а)
 ;
б)
;
б) ;
в)
;
в)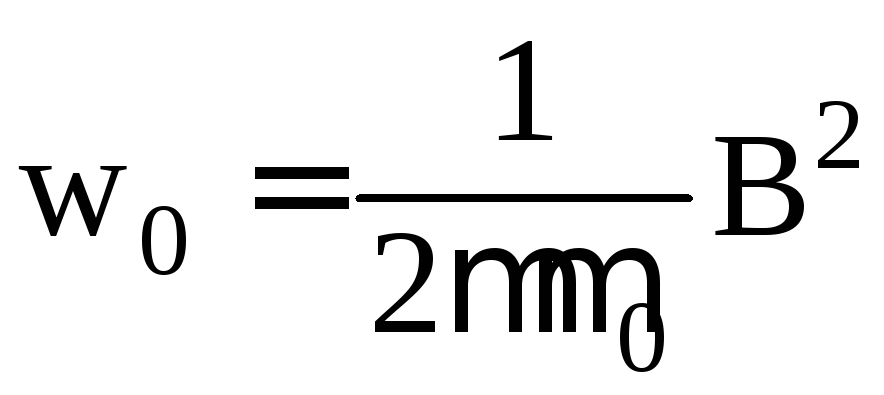 .
.
142.
Выражение
 отображает энергию неоднородного
магнитного поля:
отображает энергию неоднородного
магнитного поля:
а) занимающего элементарный объём пространства dV; б) занимающего какой-либо объём пространства V; в) занимающего всё пространство.
143. Уравнение движения частицы в электрическом поле имеет вид:
а)
 ;
б)
;
б)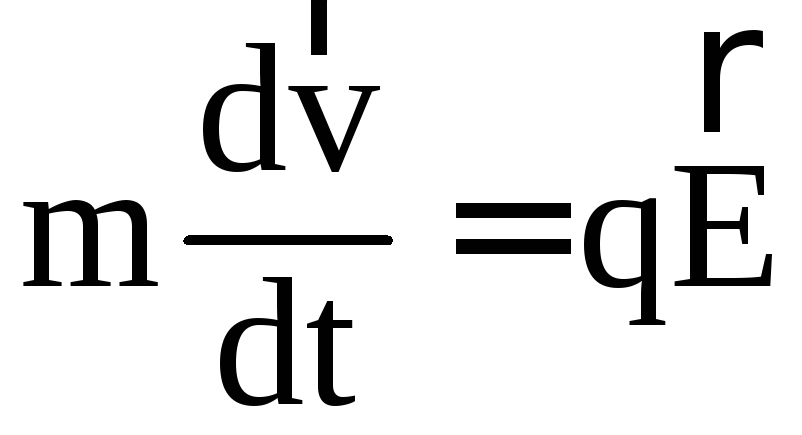 ;
в)
;
в)![]() ,
где
,
где![]() ускорение, приобретаемое частицей под
действием сил электрического поля.
ускорение, приобретаемое частицей под
действием сил электрического поля.
144. Уравнения движения заряженной частицы в электрическом поле плоского конденсатора в направлении x (в направлении перпендикулярном вектору напряженности электрического поля) имеет вид:
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.
145. Уравнения движения заряженной частицы в электрическом поле плоского конденсатора в направлении y (в направлении, совпадающем с направлением вектора напряженности электрического поля) имеет вид:
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.
146. Уравнение траектории движения заряженной частицы в электрическом поле плоского конденсатора имеет вид:
а)
 ;
б)
;
б)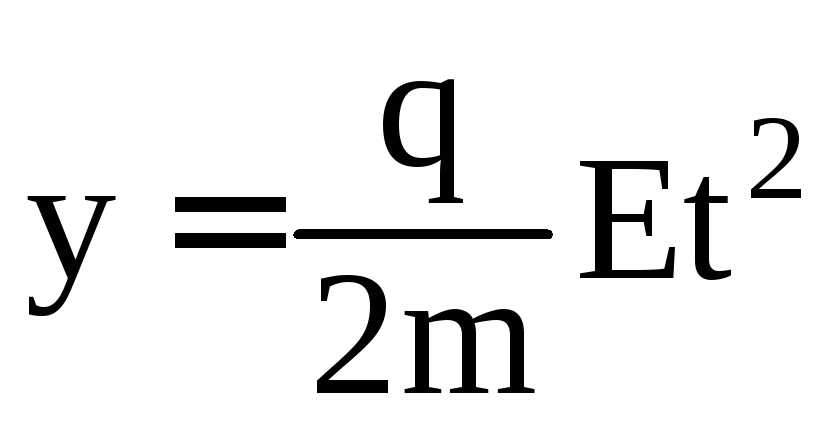 ;
в)
;
в) ;
г)
;
г) .
.
147. Тангенс угла отклонения заряженной частицы от первоначального направления при ее движении в электрическом поле плоского конденсатора можно определить по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
148. Скорость частицы в электрическом поле плоского конденсатора в направлении x (в направлении перпендикулярном вектору напряженности электрического поля):
а)
![]() ;
б)
;
б) ;
в)
;
в)![]() .
.
149. Скорость частицы в электрическом поле плоского конденсатора в направлении y (в направлении, совпадающем с направлением вектора напряженности электрического поля):
а)
 ;
б)
;
б) ;
в)
;
в) .
.
1 50.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
50.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 51.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
51.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 52.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
52.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 53.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
53.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 54.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
54.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 55.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
55.
Отрицательно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 56.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
56.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
1 57.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
57.
Положительно заряженная частица влетает
со скоростьюv0
в электрическое поле плоского конденсатора,
так как показано на рисунке. После
прохождения электрического поля скорость
частицы v
будет иметь направление:
а) 1; б) 2; в) 3.
158. Сила, действующая на заряженную частицу со стороны магнитного поля:
а) пропорциональна величине заряда;
б) пропорциональна скорости частицы;
в) пропорциональна индукции магнитного поля;
г) пропорциональна косинусу угла между направлениями векторов скорости v и индукции магнитного поля B.
159. Сила Лоренца определяется по формулам:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
160. Если скорость заряженной частицы, движущейся в однородном магнитном поле, v = 0, то сила Лоренца:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
161. Если заряженная частица движется вдоль силовой линии однородного магнитного поля, то:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
162. Если движение заряженной частицы происходит перпендикулярно силовым линиям однородного магнитного поля, то сила Лоренца:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
163. Так как сила Лоренца перпендикулярна скорости движения заряженной частицы, следовательно, к любому участку траектории движения (элементу перемещения), то она….
а) не совершает работу; б) не изменяет кинетическую энергию; в) изменяет скорость частицы.
164. Если скорость заряженных частиц перпендикулярна направлению однородного магнитного поля, то движение частиц в этом случае происходит :
а) по прямой; б) по эллипсу; в) по окружности.
165. Радиус окружности, по которой движется заряженная частица в однородном магнитном поле определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
166. Период обращения частицы при ее движении в однородном магнитном поле – время, за которое частица сделает один полный оборот определяется соотношением:
а)
![]() ;
б)
;
б) ;
в)
;
в) .
.
167. Частота обращения частицы при ее движении в однородном магнитном поле – число оборотов, совершаемых частицей, движущейся в однородном магнитном поле по окружности определяется по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
168. Движение заряженных частиц в однородном магнитном поле, если скорость частицы направлена под углом к магнитному полю, происходит:
а) по винтовой линии (спирали); б) по окружности; в) по прямой линии.
169. Шаг винтовой линии (спирали), при движении заряженных частиц в однородном магнитном поле, если скорость частицы направлена под углом к магнитному полю, определяется соотношением:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
170. Формула для определения силы, действующей на движущийся точечный заряд q в электромагнитном поле (формула Лоренца) имеет вид:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
1 71.
В однородное магнитное поле влетает
положительно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
71.
В однородное магнитное поле влетает
положительно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
а) 1; б) 2; в) 3; г) 4.
1 72.
В однородное магнитное поле влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
72.
В однородное магнитное поле влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
а) 1; б) 2; в) 3; г) 4.
1 73.
В однородное магнитное поле влетает
положительно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
73.
В однородное магнитное поле влетает
положительно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
а) 1; б) 2; в) 3; г) 4.
1 74.
В однородное магнитное поле влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
74.
В однородное магнитное поле влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите
направление отклонения этой частицы
после прохождения магнитного поля:
а) 1; б) 2; в) 3; г) 4.
1 75.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
положительно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
75.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
положительно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
а) 1; б) 2; в) 3; г) 4.
1 76.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
76.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
а) 1; б) 2; в) 3; г) 4.
1 77.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
положительно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
77.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
положительно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
а) 1; б) 2; в) 3; г) 4.
1 78.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
78.
В однородные взаимно перпендикулярные
электрическое и магнитное поля влетает
отрицательно заряженная частица, так
как показано на рисунке. Укажите наиболее
вероятное направление движения этой
частицы после прохождения полей:
а) 1; б) 2; в) 3; г) 4.
1 79.
На рисунке указаны траектории заряженных
частиц, имеющих одинаковую скорость и
влетающих в однородное магнитное поле,
перпендикулярно плоскости чертежа. При
этом для частицы 1:
79.
На рисунке указаны траектории заряженных
частиц, имеющих одинаковую скорость и
влетающих в однородное магнитное поле,
перпендикулярно плоскости чертежа. При
этом для частицы 1:
а) q>0; б) q=0; в) q<0.
1 80.
В однородное постоянное магнитное поле
дважды влетает положительно заряженная
частица. В первом случае её скоростьv1
и траектория движения представлена на
рисунке 1. Во втором случае её скорость
v2
и траектория движения представлена на
рисунке 2. В этих случаях скорость
частицы:
80.
В однородное постоянное магнитное поле
дважды влетает положительно заряженная
частица. В первом случае её скоростьv1
и траектория движения представлена на
рисунке 1. Во втором случае её скорость
v2
и траектория движения представлена на
рисунке 2. В этих случаях скорость
частицы:
а) v1>v2; б) v1=v2; в) v1<v2.
181. Если электрическое и магнитное поля взаимно перпендикулярны, то скорость дрейфа частицы в этом случае можно определить по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
182. Собственные электромагнитные колебания происходят в колебательном контуре, в котором отсутствует:
а) индуктивное сопротивление L; б) ёмкостное сопротивление 1/C; в) активное сопротивление R.
183. Дифференциальное уравнение собственных электромагнитных колебаний имеет вид:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
184. Уравнение, согласно которому происходит изменение заряда в контуре, в котором возникают собственные электромагнитные колебания, имеет вид:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
185. Уравнение, согласно которому происходит изменение напряжения в контуре, в котором возникают собственные электромагнитные колебания, имеет вид:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
186. Уравнение, согласно которому происходит изменение тока в контуре, в котором возникают собственные электромагнитные колебания, имеет вид:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
187. Частота собственных электромагнитных колебаний определяется соотношением:
а)
![]() ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)![]() .
.
188. Период собственных электромагнитных колебаний определяется соотношением:
а)
![]() ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)![]() .
.
189. Затухающие электромагнитные колебания происходят в колебательном контуре, в котором:
а) отсутствует индуктивное сопротивление L, ёмкостное сопротивление 1/C, активное сопротивление R;
б) имеется только ёмкостное сопротивление 1/C; в) имеются индуктивное сопротивление L, ёмкостное сопротивление 1/C, активное сопротивление R; г) отсутствует индуктивное сопротивление L, имеется ёмкостное сопротивление 1/C, отсутствует активное сопротивление R.
190. Принято считать, что при затухающих электромагнитных колебаниях энергия колебательного контура рассеивается (теряется) только:
а) на индуктивном сопротивлении L; б) на ёмкостном сопротивлении 1/C; в) на активном сопротивлении R
191. При затухающих электромагнитных колебаниях энергия колебательного контура:
а) не восполняется извне; б) восполняется извне; в) остаётся величиной постоянной.
192. Дифференциальное уравнение затухающих электромагнитных колебаний имеет вид:
а)
 ;
б)
;
б) ;
;
в)
 .
.
193. Уравнение, согласно которому происходит изменение заряда в контуре, в котором существуют затухающие электромагнитные колебания имеет вид:.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() .
.
194. Условная циклическая частота затухающих электромагнитных колебаний определяется по формуле:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
195. Период затухающих электромагнитных колебаний определяется соотношением:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
196. Декремент затухания электромагнитных колебаний:
а) отношение двух последовательных максимальных значений электрического заряда колебательного контура;
б) отношение двух последовательных максимальных значений электрического заряда колебательного контура, отличающихся по времени на период;
в) отношение двух последовательных значений электрического заряда колебательного контура, отличающихся по времени на период.
197. Вынужденные электромагнитные колебания совершаются в колебательном контуре, в котором:
а) действует вынуждающая сила (ЭДС), не изменяющаяся с течением времени;
б) действует вынуждающая сила (ЭДС), изменяющаяся по какому-либо периодическому закону (например, по закону синуса или косинуса);
в) действует вынуждающая сила (ЭДС), уменьшающаяся с течением времени.
198. Дифференциальное уравнение вынужденных электромагнитных колебаний может иметь вид:
а)
 ;
б)
;
б) ;
;
в)
 .
.
199. Амплитудное значение заряда в колебательном контуре, в котором происходят вынужденные электромагнитные колебания, определяется по формуле:
а)
 ;
б)
;
б) ;
;
в)
 .
.
200. Фаза вынужденных электромагнитных колебаний определяется соотношением:
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)
 .
.
201. Резонанс это явление резкого возрастания амплитудных значений при электромагнитных колебаниях в колебательном контуре:
а) только заряда; б) только тока; в) только напряжения; г) всех переменных величин.
202. Амплитуда напряжения, в колебательном контуре, в котором существуют электромагнитные колебания, определяются по формуле:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
203. Амплитуда тока, в колебательном контуре, в котором существуют электромагнитные колебания, определяются по формуле:
а)
 ;
б)
;
б) ;
;
в)
 .
.
204. Амплитуда индуцируемой ЭДС, в колебательном контуре, в котором существуют электромагнитные колебания, определяются по формуле:
а)
![]() ;
б)
;
б) ;
в)
;
в)
205.
Резонансная частота (![]() )
это:
)
это:
а) частота, соответствующая максимальному значению q01;
б) частота, соответствующая максимальному значению тока;
в) частота, соответствующая максимальному значению напряжения.
206. Автоколебания – вынужденные незатухающие колебания в реальных системах, период и амплитуда которых:
а) не зависят от характера внешнего воздействия;
б) определяются свойствами самой автоколебательной системы;
в) зависят от характера внешнего воздействия и не зависят от свойств самой колебательной системы.
207. Электромагнитные волны это:
а) процесс распространения электромагнитных колебаний в пространстве с конечной скоростью;
б) процесс распространения электромагнитных колебаний в пространстве с любой скоростью;
в) процесс распространения переменного электромагнитного поля в пространстве с конечной скоростью;
г) процесс распространения переменного электромагнитного поля в пространстве с любой скоростью.
208. Длина электромагнитной волны это:
а) расстояние между двумя точками, колебания в которых отличаются по фазе на ;
б) расстояние между двумя точками, в которых амплитуда изменяющихся параметров колебаний достигают либо максимума, либо минимума;
в) расстояние, на которое распространяется волна за время одного периода колебания T.
209. Поперечность электромагнитных волн заключается в том, что:
а) вектор напряженности электрического поля E и вектор напряженности магнитного поля H взаимно перпендикулярны и лежат в плоскости, вектора скорости распространения электромагнитной волны v;
б) вектор напряженности электрического поля E и вектор напряженности магнитного поля H взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости распространения электромагнитной волны v;
в) вектор напряженности электрического поля E и вектор скорости распространения электромагнитной волны v взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору напряженности магнитного поля H.
210. Векторы напряженностей E и H переменного электромагнитного поля удовлетворяют волновым уравнениям типа:
а)
 ;
б)
;
б) ;
;
в )
) ;
г)
;
г) ,
где
,
где – фазовая скорость;
– фазовая скорость;
211.
На рисунке показана ориентация векторов
напряженности электрического E
и магнитного H
полей в электромагнитной волне. Вектор
плотности потока энергии электромагнитной
волны
![]() ориентирован в направлении:
ориентирован в направлении:
а) 4; б) 3; в) 2; г) 1.
2 12.
На рисунке показана ориентация векторов
напряженности электрическогоE
и магнитного H
полей в электромагнитной волне. Вектор
плотности потока энергии электромагнитной
волны
12.
На рисунке показана ориентация векторов
напряженности электрическогоE
и магнитного H
полей в электромагнитной волне. Вектор
плотности потока энергии электромагнитной
волны
![]() ориентирован в направлении:
ориентирован в направлении:
а) 4; б) 3; в) 2; г) 1.
213. Первое положение теории Максвелла утверждает: «Переменные электрическое и магнитное поля:
а) могут существовать отдельно»;
б) не могут существовать отдельно»;
в) могут существовать независимо друг от друга»;
г) они существуют всегда вместе в виде единого электромагнитного поля».
214. Второе положение теории Максвелла утверждает: «Электромагнитное поле, возникнув в одном месте пространства:
а) не остается локализованным в нем»;
б) остаётся локализованным в нём»;
в) распространяется от этого места в виде электромагнитной волны»;
г) не распространяется от этого места в виде электромагнитной волны».
215.
Вихревое электрическое поле, для которого
справедливо соотношение
 ,
гдеEB
– вектор напряженности вихревого
электрического поля, возникает в
проводниках. Оно обусловлено:
,
гдеEB
– вектор напряженности вихревого
электрического поля, возникает в
проводниках. Оно обусловлено:
а) наличием постоянного тока в проводниках;
б) наличием переменного тока в проводниках;
в) явлением электромагнитной индукции
216.
Ток смещения
 ,
гдеD
– вектор индукции электрического поля,
это:
,
гдеD
– вектор индукции электрического поля,
это:
а) изменяющееся со временем электрическое поле, которое порождает магнитное поле так же, как и ток проводимости;
б) изменяющийся со временем электрическое ток, который порождает магнитное поле так же, как и ток проводимости;
в) это постоянный ток проводимости, который порождает магнитное поле.
217.
Плотность тока смещения в диэлектриках
 ,
где :
,
где :
а)
 – плотность тока проводимости в вакууме;
– плотность тока проводимости в вакууме;
б)
 – плотность тока смещения в вакууме;
– плотность тока смещения в вакууме;
в)
![]() – плотность тока поляризации (тока,
обусловленного упорядоченным движением
электрических зарядов в диэлектрике);
– плотность тока поляризации (тока,
обусловленного упорядоченным движением
электрических зарядов в диэлектрике);
г)
![]() – плотность тока поляризации, который
представляет собой смещение зарядов в
неполярных молекулах, поворот диполей
в полярных молекулах.
– плотность тока поляризации, который
представляет собой смещение зарядов в
неполярных молекулах, поворот диполей
в полярных молекулах.
218.
Первое уравнение Максвелла
 ,
где
,
где – циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;E=Eq+EB
– вектор напряженности результирующего
электрического поля; Eq
– напряженность потенциального
электрического поля (электрического
поля, порождаемого электрическими
зарядами); EB
– напряженность вихревого электрического
поля, показывает, что:
– циркуляция вектора напряженности
результирующего поля, потенциального
и вихревого;E=Eq+EB
– вектор напряженности результирующего
электрического поля; Eq
– напряженность потенциального
электрического поля (электрического
поля, порождаемого электрическими
зарядами); EB
– напряженность вихревого электрического
поля, показывает, что:
а) источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля;
б) источниками электрического поля могут быть не только электрические заряды, но и не изменяющиеся во времени магнитные поля;
в) оно выражает закон электромагнитной индукции:
219.
Второе уравнение Максвелла
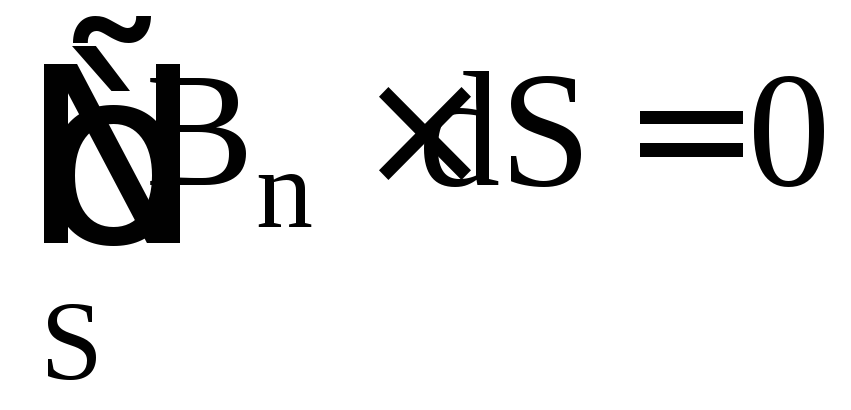 отражает
свойство вектораB,
согласно которому:
отражает
свойство вектораB,
согласно которому:
а) линии вектора В разомкнуты; б) линии вектора В замкнуты; в) линии вектора В уходят в бесконечность.
220.
Третье уравнение
 устанавливает:
устанавливает:
а) связь между токами проводимости и смещения и порождаемым ими магнитным полем;
б) только связь между токами проводимости и смещения;
в) связь между током проводимости и порождаемым им магнитным полем.
221.
Четвертое уравнение Максвелла
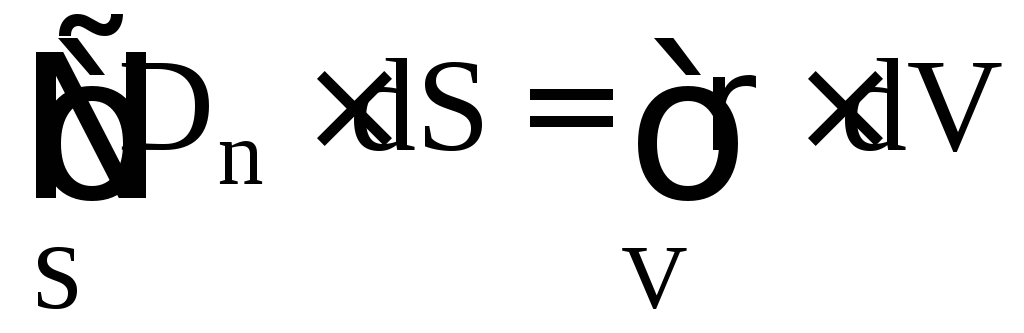 :
:
а) показывает, что линии вектора D могут начинаться и оканчиваться на зарядах ;
б) показывает, что линии вектора D не могут начинаться и оканчиваться на зарядах;
в) отображает теорему Остроградского-Гаусса для вектора D.
222.
Система уравнений Максвелла в
дифференциальной форме:
 ;
;![]() ;
; ;
;![]() справедлива для переменного
электромагнитного поля:
справедлива для переменного
электромагнитного поля:
а) в отсутствие заряженных тел; б) при наличии заряженных тел и токов проводимости; в) в отсутствие заряженных тел и токов проводимости; г) в отсутствие токов проводимости.
223.
Следующая система уравнений Максвелла:
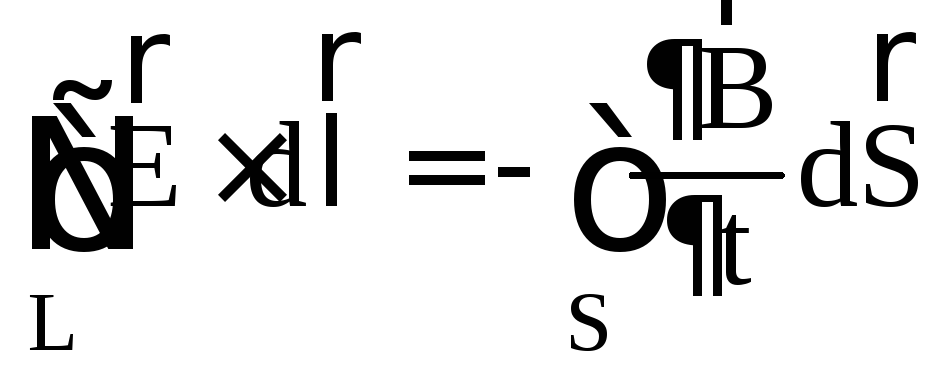 ;
; ;
; ;
; справедлива для переменного
электромагнитного поля:
справедлива для переменного
электромагнитного поля:
а) в отсутствие заряженных тел; б) при наличии заряженных тел и токов проводимости; в) в отсутствие заряженных тел и токов проводимости; г) в отсутствие токов проводимости.
224.
Полная система уравнений Максвелла для
электромагнитного поля имеет вид:
 ;
; ;
; ;
; .
Следующая система уравнений:
.
Следующая система уравнений: ;
; ;
; ;
; справедлива для переменного
электромагнитного поля:
справедлива для переменного
электромагнитного поля:
а) в отсутствие заряженных тел; б) в отсутствие заряженных тел и токов проводимости; в) в отсутствие токов проводимости; г) при наличии заряженных тел и токов проводимости.
225.
Материальные уравнения 1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() :
:
а) используются при решении уравнений Максвелла; б) первое связывает векторы напряженности и индукции электрического поля; в) второе связывает векторы индукции и напряженности магнитного поля;
г) третье отображает закон Ома в дифференциальной форме.
226.
Закон сохранения электрического заряда
 утверждает: «Полный ток, протекающий
за единицу времени через любую замкнутую
поверхностьS,
равен изменению заряда внутри объема
V,
ограниченного поверхностью S».
Если ток через поверхность отсутствует,
то:
утверждает: «Полный ток, протекающий
за единицу времени через любую замкнутую
поверхностьS,
равен изменению заряда внутри объема
V,
ограниченного поверхностью S».
Если ток через поверхность отсутствует,
то:
а) заряд в объеме V уменьшается; б) заряд в объеме V увеличивается; в) заряд в объеме V остается неизменным.
227.
Закон сохранения энергии для
электромагнитного поля
 утверждает: «Изменение энергии
электромагнитного поля в некотором
объемеV
равно сумме потока энергии электромагнитного
поля и количества теплоты, выделившейся
в этом объеме», где:
утверждает: «Изменение энергии
электромагнитного поля в некотором
объемеV
равно сумме потока энергии электромагнитного
поля и количества теплоты, выделившейся
в этом объеме», где:
а) w – энергия поля; б) Пn – проекция вектора Пойтинга-Умова на направление положительной нормали к поверхности dS; в) Q – количество тепла, выделяемое в единицу времени.
228. Принцип относительности: «Электромагнитные явления протекают:
а) в различных инерциальных системах по-разному; б) одинаково во всех инерциальных системах отсчета; в) в различных неинерциальных системах по-разному.
229. Инвариантность уравнений Максвелла относительно преобразований Лоренца:
а) уравнения Максвелла не меняют своей формы при переходе от одной инерциальной системы отсчета к другой инерциальной системе отсчета;
б) уравнения Максвелла изменяют свою форму при переходе от одной инерциальной системы отсчета к другой инерциальной системе отсчета;
в) уравнения Максвелла не меняют своей формы при переходе от одной неинерциальной системы отсчета к другой неинерциальной системе отсчета.
230. Пространственные координаты, время, векторы электромагнитного поля E, H, B, D, плотность тока j и объемная плотность заряда :
а) не изменяются в соответствии с преобразованиями Лоренца; б) уменьшаются соответствии с преобразованиями Лоренца; в) изменяются в соответствии с преобразованиями Лоренца; г) увеличиваются в соответствии с преобразованиями Лоренца.
