2.1. Циркуляция индукции магнитного поля. Вихревой характер магнитного поля. Теорема о циркуляции индукции магнитного поля (закон полного тока для магнитного поля)

Циркуляцией вектора напряженности магнитного поля по замкнутому контуру L (или просто циркуляцией вектора напряженности магнитного поля) называют интеграл

.

И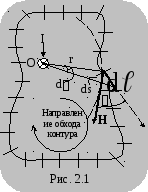з закона Био-Савара-Лапласа и принципа суперпозиции магнитных полей как экспериментальных факторов вытекает важное следствие, которое облегчает расчеты магнитных полей. Для установления этого следствия проведем в магнитном поле некоторую замкнутую линию L (контур произвольной формы и произвольных размеров) (рис. 2.1). Разобьем ее на элементарные участки. Для каждого из участков составим произведение,где - угол между направлениемH и касательной к контуру. Проинтегрировав, получим

. (2.1)

С учетом того что напряженность магнитного поля от бесконечно длинного проводника с током , а, имеем

.

Таким образом,

. (2.2)

При изменении направления тока в проводнике в каждой точке поля вектор H изменит свое направление на обратное. Косинусы углов будут иметь противоположный знак, и интеграл будет отрицательным. Знак интеграла изменится также и при перемене направления обхода контура L, вследствие чего изменятся направления касательных. Ввиду этого направление обхода и направление тока должны быть связаны между собой правилом "правого винта».

Если внутри замкнутого контура находятся n токов, то

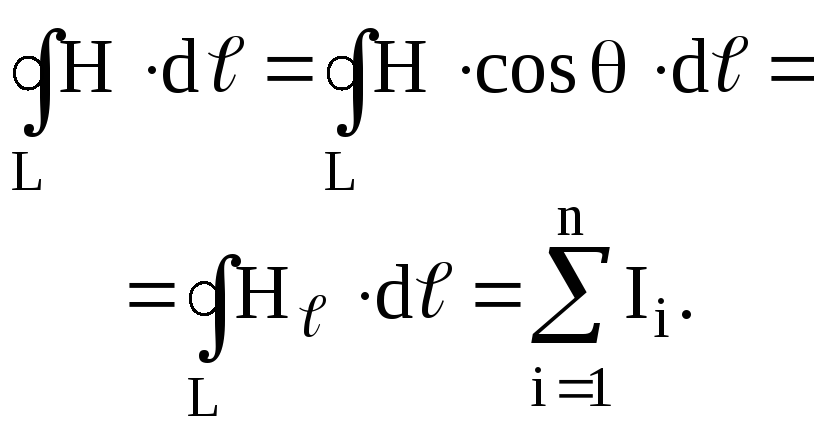(2.3)

Если ток протекает вне контура (рис. 2.2), то в этом случае можно записать

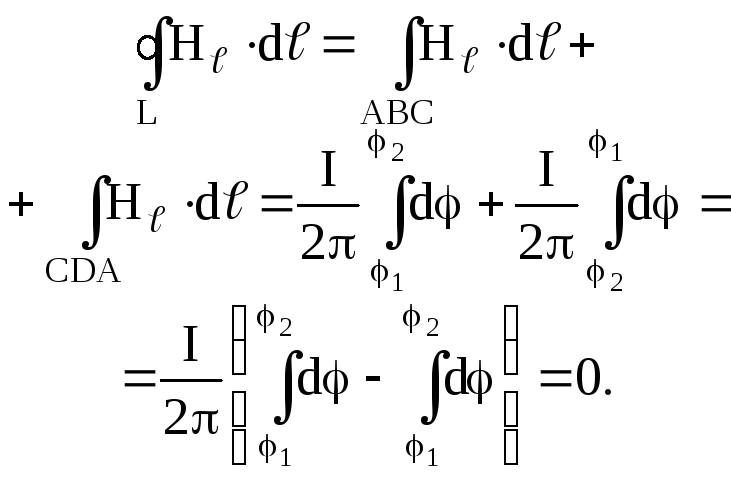
(2.4)

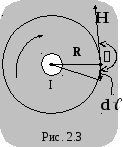
Соотношение справедливо и в том случае, когда контур и проводник имеют произвольную форму. Если ток направлен «на нас», то векторнаправлен «против часовой стрелки» (рис. 2.3). В этом случаеи. В результате получим

. (2.5)

Е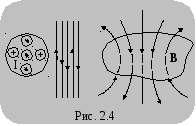сли же контур охватываетпроводников с токами, направленными в разные стороны, то, учитывая, что от положения проводника внутри контура не зависит циркуляция, можем мысленно собрать все проводники в «жгут», толщина которого в силу конечности мала. По «жгуту» протекает ток, равный алгебраической сумме токов отдельных проводников (рис. 2.4).

Утверждение (2.3), что циркуляция вектора напряженности магнитного поля по замкнутому контуру L равна алгебраической сумме токов, охватываемых контуром, называется теоремой о циркуляции магнитного поля или законом полного тока в интегральной форме. Таким образом, из закона полного тока вытекают следующие следствия:

а) если направление обхода контура и направление тока в проводнике не связаны между собой правилом правого винта, то значение

,

сохранив величину, изменит знак;

б) если контур, расположенный в магнитном поле, не охватывает ток или алгебраическая сумма токов внутри замкнутого контура равна нулю, то

.

Зная связь между вектором напряженности H и вектором индукции B магнитного поля, можно записать закон полного тока в интегральной форме для циркуляции вектора индукции:

. (2.6)

Так как ,, то магнитному полю нельзя приписать какой-либо потенциал, а это означает, что магнитное поле является вихревым, а не потенциальным.

Закон полного тока в виде (2.3) и (2.6) для вакуума в стационарном случае является непосредственным следствием закона Био-Савара-Лапласа и может быть проверен экспериментально. Этот закон был выведен для тока, текущего по прямому, бесконечно длинному проводу.

О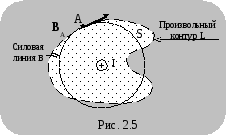казывается, что закон полного тока справедлив для произвольных токов и контуров (например, такого, который показан на рис. 2.5). Для доказательства данного утверждения необходимо получить его в дифференциальной форме, что в данной лекции не рассматривается.

Отметим, что для вычисления силы полного тока можно выбрать любую поверхность S, ограниченную замкнутым контуром L.

Уравнение (2.6) было получено исходя из закона Кулона, принципа суперпозиции электрических полей, инвариантности заряда и формул теории относительности. Можно показать, что закон Био-Савара-Лапласа можно получить из уравнения (2.6) как решение этого уравнения в случае отсутствия токов на бесконечности.