1.3. Применение закона Био-Савара-Лапласа к расчету магнитных полей прямолинейного и кругового токов

1.3.1. Магнитное поле прямолинейного бесконечно длинного проводника с током

Определим напряженность магнитного поля, порождаемого бесконечно длинным проводником с током I, в точке А, равноудаленной от его концов (рис. 1.4,а). Для чего выделим некоторый участок проводника длиной, а рассматриваемую точку расположим на кратчайшем расстоянии r₀ от него. На основании закона Био-Савара-Лапласа каждый элемент проводника в рассматриваемой точке создает магнитное поле с напряженностью (рис. 1.4,б):

, (1.18)

где I - величина тока в проводнике;

r - расстояние от элемента проводника dl до рассматриваемой точки поля;

 - угол между направлением тока в проводнике и направлением на рассматриваемую точку поля;

=  - численное значение вектора, равного элементу проводника, направление которого совпадает с направлением тока.

Из рис. 1.4,б видно, что

; .

Тогда

. (1.19)

Применив принцип суперпозиции магнитных полей, проинтегрировав выражение (1.19) в пределах от ₁ до ₂ (где ₁ и ₂ – соответственно углы между направлением тока в проводнике и направлением на рассматриваемую точку поля), получим

. (1.20)

При симметричном расположении точки М относительно концов проводника cos₁ = - cos₂, тогда

, (1.21)

где

.

Для бесконечно длинного проводника ₁0, ₂, тогда

. (1.22)

Направление векторов исовпадает с направлением касательной к цилиндрической поверхности радиусаr. По мере удаления от проводника иубывают по гиперболе (рис. 1.5).

Зная связь между напряженностью и индукцией магнитного поля, можно получить соответствующие формулы для определения индукции магнитного поля:

;

; . (1.23)

Параметры магнитного поля иостаются постоянными для любой точки, лежащей на цилиндрической поверхности, которой принадлежит точкаи ось которой совпадает с осью проводника. Это обусловлено цилиндрической симметрией магнитного поля бесконечного линейного тока (рис. 1.6).

1.3.2. Магнитное поле на оси кругового проводника с током

Магнитное поле на оси кругового проводника радиусом R, в котором существует ток I, является результирующим полем от всех элементов проводника (рис. 1.7). Каждый из диаметрально противоположных элементарных участков в точке, лежащей на оси проводника, создает свое собственное поле с напряженностью dH^'. Вектор dH направлен под углом  к оси проводника. Разложим dH на две составляющие: dH_II, направленную вдоль оси, и dH_, перпендикулярную ей. Из рисунка можно установить, что для каждой пары диаметрально противоположных участков составляющие dH_ равны по величине и противоположны по направлению, а составляющие dH_II равны по величине и одинаково направлены. Поэтому при геометрическом сложении элементарных напряженностей dH от всех участков составляющие dH_ взаимно уничтожаются и результирующая напряженность магнитного поля H в точке на оси кругового проводника будет равна алгебраической сумме всех dH_II, т.е. интегралу, взятому от dH_II по всему круговому контуру :

. (1.24)

Численное значение

, (1.25)

где R - радиус кругового проводника;

r - расстояние от элемента проводника до рассматриваемой точки поля.

Учитывая, что по закону Био-Савара-Лапласа и что = 90^o, можем записать

.

Подставляя последнее выражение в формулу (1.24) и учитывая, что I, R и r для всех участков кругового проводника одинаковы, получим

. (1.26)

Так как = 2R; , то окончательное выражение напряженности поля примет вид

. (1.27)

В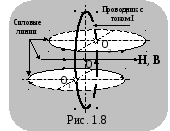ектор напряженности магнитного поля направлен вдоль оси кругового проводника с током.

Отметим, что при r_o = 0, т.е. в центре кругового проводника, напряженность магнитного поля

. (1.28)

На рис. 1.8 показана картина линий напряженности магнитного поля кругового тока.

Для нахождения направления векторов ив точках, лежащих на оси, применяется «правило буравчика»: буравчик располагается вдоль оси кругового тока и вращается по направлению тока, поступательное движение его укажет направление,.