1.2. Закон Био-Савара-Лапласа

1.2.1. Магнетизм как релятивистский эффект

П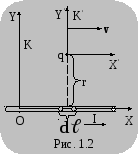усть в неподвижной системе отсчетавдоль осирасположен проводник с током (рис. 1.2). Выделим на проводнике элемент длиной. Если поперечное сечение проводника, концентрация носителя заряда,- элементарный заряд (например, заряд протона), то в объеме элементанаходится электрический заряд

.

Будем считать скорость направленного движения зарядов в проводнике равной . Предположим, что на расстоянииот выделенного элемента проводникав подвижной системесо скоростьюдвижется электрический заряд. Направление движения системы(заряда) совпадает с направлением тока в проводнике (элементе проводника).

Между силами, действующими на заряд в подвижной и неподвижной системах отсчета (с точки зрения специальной теории относительности), существует связь

,

где - сила, действующая на заряд в неподвижной системе отсчета;

- сила, действующая на заряд в подвижной системе отсчета.

На основании закона Кулона можно записать

,

тогда

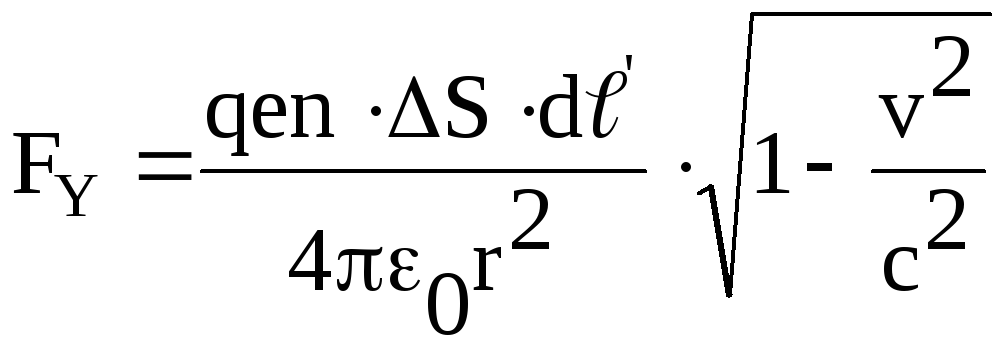. (1.9)

Принимая во внимание Лоренцево сокращение элемента , фиксируемое наблюдателем, находящимся в системе, заменим в уравнении (1.9)на

.

Будем иметь

. (1.10)

Первое слагаемое в выражении (1.10) представляет собой кулоновскую силу взаимодействия двух точечных зарядов:

.

Это слагаемое значительно превосходит второе слагаемое, однако оказывается полностью скомпенсированным кулоновской силой, действующей на заряд со стороны ионов, образующих кристаллическую решётку (любой элемент проводника электрически нейтрален). Не-скомпенсированным остаётся второе слагаемое формулы (1.10), обусловленное магнитным взаимодействием движущихся зарядов:

. (1.11).

Знак «минус» в выражении (1.11) означает, что сила магнитного взаимодействия (магнитная сила) в данном случае является силой притяжения. В то время как кулоновская сила (в данном случае) является силой отталкивания.

Таким образом, с точки зрения теории относительности, между движущимися электрическими зарядами, помимо силы электрического происхождения, действует сила магнитного происхождения. Это позволяет утверждать, что в пространстве вокруг движущихся зарядов существует магнитное поле.

1.2.2. Закон Био-Савара-Лапласа и алгоритм его применения

Из основных положений теории относительности было получено выражение для численного значения магнитной составляющей силы взаимодействия заряда и элемента тока:

. (1.11^')

Обозначив постоянную Гн/ми учитывая, что, перепишем формулу (1.11^') в виде

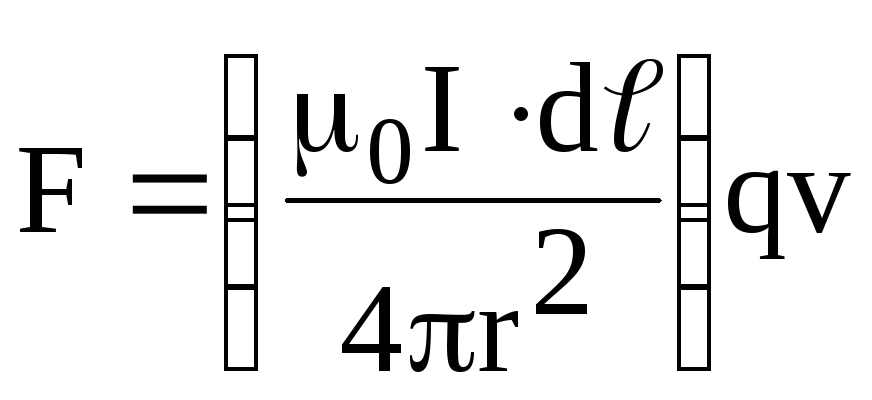. (1.12).

Два последних сомножителя в (1.12) являются электрическим и кинетическим параметрами заряда , а сомножитель в скобках характеризует магнитную компоненту электромагнитного поля, т.е. представляет элемент индукции магнитного поля. Таким образом

. (1.13).

Следовательно, магнитное поле действительно является проявлением (частью) более общего электромагнитного поля. При этом очень существенным оказывается выбор системы отсчета. Так, например, если в данной системе отсчета заряд покоится (), то магнитного поля вокруг этого заряда не существует. При переходе в подвижную систему отсчета, с которой связан движущийся электрический заряд, появляется магнитная компонента электромагнитного поля (). Выражение (1.13) представляет элемент индукции магнитного поля для частного случая, когда интересующие точки поля лежат на перпендикуляре к элементу.

Еще до появления теории относительности Лаплас, обобщив результаты экспериментальных исследований, проведенных Био и Саваром, предложил формулу для расчета элемента индукции магнитного поля в общем случае

, (1.14).

где α- угол между направлениями радиус-вектора, проведенного из элемента тока в интересующую точку пространства, и элементом тока (рис. 1.3);

- магнитная проницаемость вещества, безразмерная величина (для вакуума ).

Из сопоставления формул (1.13) и (1.14) видно, что формула (1.13) является частным случаем формулы (1.14).

В векторной форме закон Био-Савара-Лапласа для элемента индукции магнитного поля можно записать так:

. (1.15).

Поскольку является результатом векторного произведения векторови, то он перпендикулярен к плоскости, образованной векторами-сомножителями, а его направление можно определить с помощью правила правого винта.

Учитывая связь между вектором напряженности магнитного поля и вектором индукции магнитного поля(1.7), для элемента напряженностизакон Био-Савара-Лапласа можно записать в виде

(1.16)

или в векторной форме

. (1.17)

Чтобы получить значение вектора индукции (напряженности) магнитного поля, обусловленного произвольным проводником с током, необходимо этот проводник представить в виде совокупности элементов тока, записать выражение для элемента индукции (напряженности) магнитного поля, а затем произвести суммирование по всем элементам индукции (напряженности), т.е.

или .

В этом смысл алгоритма применения закона Био-Савара-Лапласа для расчета магнитных полей, обусловленных постоянным током, и принципа суперпозиции магнитных полей, согласно которому если магнитное поле создано несколькими токами, то результирующее поле характеризуется результирующими векторами B или H, которые определяются (согласно принципу суперпозиции магнитных полей) так:

и . (1.8)