6.2. Получение электромагнитных колебаний. Собственные электромагнитные колебания. Дифференциальное уравнение собственных электромагнитных колебаний и его решение

Известно, что колебательные движения – это такие движения, которые отличаются той или иной степенью повторяемости.

Рассматривая механические колебания, было установлено, что переменными величинами в них могут быть: смещение, амплитуда, фаза и другие величины.

В электромагнитных колебаниях периодически изменяющимися величинами являются: заряды, токи, напряжения, электрические и магнитные поля, связанные с токами.

Э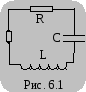лектромагнитные колебания получают в устройствах, которые называются колебательными контурами (открытых и закрытых).

Закрытый колебательный контур представляет собой электрическую цепь, состоящую из конденсатора емкостью C, катушки (соленоида) с индуктивностью L, сопротивления R, соединенных последовательно (рис. 6.1).

Рассмотрим закрытый колебательный контур, состоящий только из конденсатора емкостью C и катушки с индуктивностью L (рис. 6.2).

Для получения электромагнитных колебаний в такой цепи необходимо предварительно зарядить конденсатор.

В начальный момент времени t = 0: ток в цепи отсутствует I = 0, в конденсаторе существует электрическое поле с максимальным значением напряженности E = E_m и энергией

. (6.8)

После замыкания ключа «К», конденсатор начнет разряжаться, в контуре появится возрастающий электрический ток I, а в катушке индуктивности – магнитное поле с возрастающим значением напряженности H (индукции B). Таким образом, по мере разрядки конденсатора его электрическое поле ослабевает, а магнитное поле катушки увеличивается.

В момент времени конденсатор полностью разрядится. Электрическое поле в нем будет отсутствовать (E = 0). Величина тока достигнет максимального значения I = I_m. Напряженность магнитного поля катушки достигнет максимального значения H = H_m. Максимальной будет и энергия магнитного поля:

. (6.9)

Затем магнитное поле будет ослабевать. На основании закона электромагнитной индукции в цепи будет возникать индукционный ток, направление которого такое же, какое имел ток разрядки конденсатора (согласно закону Ленца). Конденсатор будет перезаряжаться.

В момент времени конденсатор полностью перезарядится. Напряженность электрического поля в нем достигнет максимального значения E = E_m, хотя направление вектора E будет противоположным первоначальному направлению. Ток в контуре прекратится (I = 0). Напряженность магнитного поля соленоида станет равной нулю (H=0). Энергия контура вновь будет равна энергии электрического поля конденсатора.

Затем вновь начнет разряжаться конденсатор, в цепи появится электрический ток, направление которого противоположно току первоначальной разрядки. В катушке появится магнитное поле противоположного направления.

В момент времени конденсатор полностью разрядится. Ток прекратится. Напряженность электрического поля станет равной нулю. Магнитное поле катушки вновь достигнет максимального значения, при этомH = - H_m, т.е. энергия контура будет равна энергии магнитного поля катушки.

В последующий момент времени магнитное поле начнет ослабевать, возникнет индукционный ток, препятствующий ослаблению магнитного поля, конденсатор начнет перезаряжаться.

В момент времени система возвратится в первоначальное состояние и начнется повторение рассмотренных процессов.

Таким образом, в закрытом колебательном контуре будут существовать изменяющиеся процессы с переменными характеристиками, возникнут электромагнитные колебания, которые сопровождаются периодическими взаимными превращениями энергий электрического и магнитного полей. Эти превращения энергий подобны превращению энергий при гармонических колебаниях, например, математического маятника.

Если бы в контуре не было потерь энергии (нагревание проводников, излучения), то электромагнитные колебания в нем совершались бы по гармоническому закону, были бы незатухающими.

Электромагнитные колебания, которые происходят в самом колебательном контуре, называются собственными колебаниями.

Уравнение собственных электромагнитных колебаний можно получить из следующих соображений. Считая, что мгновенное значение силы тока во всем контуре одно и то же, на основании второго закона Кирхгофа можно записать

. (6.10)