3.1. Природа магнитных свойств вещества. Магнитные моменты атомов. Микро- и макротоки (молекулярные токи)

Известно, что некоторые вещества в магнитном поле намагничиваются, т.е. сами становятся источниками магнитного поля. Поэтому магнитное поле в веществе представляет собой результат сложения полей, создаваемых проводниками с током (макротоками) и намагниченной средой.

Причина намагничивания заключается в том, что во всех веществах существуют электрические токи, замыкающиеся в пределах каждого атома или молекулы (микротоки или молекулярные токи). На рис. 3.1 представлена модель молекулярных токов в однородно намагниченном магнетике и соответствующий им поверхностный ток.

Существование микротоков (молекулярных токов) в веществе объясняется тем, что каждый электрон совершает вращательное движение вокруг ядра с достаточно большой скоростью. Его местоположение и скорость в данный момент времени с достаточной степенью точности определить невозможно. Это означает, что вращающийся электрон представляет собой некоторый эквивалентный круговой ток, который обладает магнитным моментом.

Для расчета этого момента предположим, что орбита представляет собой окружность с радиусом r, по которой электрон движется с постоянной скоростью v_o. С учетом того что сила эквивалентного тока равна заряду электрона e, а частота обращения (число оборотов в единицу времени) , для магнитного момента электрона имеем

. (3.1)

Движущийся по орбите электрон обладает орбитальным механическим моментом импульса, значение которого можно определить по формуле

; . (3.2)

Направление векторов и определяется правилом «правого винта». Согласно этому правилу можно установить, что направления этих векторов противоположны (рис. 3.2).

Из формул (3.1), (3.2) видно, что орбитальный магнитный момент электрона пропорционален его механическому моменту импульса:

(3.3)

Отношение магнитного момента электрона к его механическому моменту количества движения (моменту импульса), т.е.

, (3.4)

называется гиромагнитным отношением. Знак «минус» в выражении (3.4) как раз и указывает на то, что направления указанных моментов противоположны. Гиромагнитное отношение, определяемое универсальными постоянными, одинаково для любого вида орбит (круговых, эллиптических), хотя для разных орбит электронов значенияv и r различны.

Экспериментально гиромагнитное отношение было определено в 1915 г. Эйнштейном и Гаазом. В опытах Эйнштейна и Гааза железный стержень, подвешенный на тонкой упругой нити, помещался внутрь соленоида (рис. 3.3). На упругой нити было закреплено зеркальце, на которое направлялся луч света. При пропускании постоянного электрического тока в соленоиде создается магнитное поле, которое намагничивает железный стержень. В результате стержень начинал поворачиваться, причем направление вращения стержня изменялось при изменении тока в соленоиде (магнитного поля внутри соленоида). Одновременно со стержнем во вращение приходит зеркальце. Отраженный луч при повороте системы смещается по шкале, установленной для повышения чувствительности на достаточно большом расстоянии. При повороте зеркальца на угол луч отклоняется на удвоенный угол 2.

Возникновение вращения при намагничивании получило название магнитомеханического эффекта. Объяснить возникновение магнитомеханического эффекта можно путем следующих рассуждений.

В ненамагниченном стержне орбиты электронов имеют произвольную ориентацию, поэтому суммарный механический момент импульса их равен 0. При намагничивании стержня плоскости молекулярных токов становятся параллельными, что приводит к возникновению суммарного момента импульса . Так как электроны и кристаллическая решетка являются замкнутой системой, для которой выполняется закон сохранения момента импульса, то должно выполняться соотношение

. (3.5)

При изменении направления магнитного поля (тока в соленоиде) происходит перемагничивание стержня, что приводит к изменению направления магнитных моментов на 180⁰, направление механического момента импульса изменяется на противоположное.

Следовательно, кристаллическая решетка и стержень должны совершать вращательное движение. Закручивание нити при намагничивании стержня постоянным магнитным полем получалось весьма малым.

Чтобы сделать вращение более эффективным, для перемагничивания используют переменный ток с частотой, равной резонансной для данной колебательной системы. В результате эксперимента было установлено, что гиромагнитное отношение

, (3.6)

т.е. в два раза больше, чем его теоретическое значение (3.4):

. (3.7)

Позднее было доказано, что полученное несоответствие между иобусловлено наличием у электронов, кроме орбитальных, собственных магнитного и механического моментов или спинов. Собственный (спиновый) механический момент и связанный с ним собственный (спиновый) магнитный момент являются такими же характеристикамиэлектрона, как его масса и заряд.

Оказалось, что их отношение

.

Спином обладают не только электроны, но и другие элементарные частицы и ядра атомов.

В атомах и молекулах различных веществ имеется множество электронов, вращающихся по орбитам. Так как магнитный момент вектор, ориентированный перпендикулярно к плоскости орбиты, то можно найти векторную сумму магнитных моментов всех электронов, входящих в состав атомов, молекул или имеющихся в единице объема данного вещества. При суммировании магнитных моментов электронов, существующих в данном атоме, молекуле или объеме вещества, необходимо учитывать не только собственные магнитные моменты самих электронов, но и моменты замкнутых орбит, описываемых электронами.

С учетом того что ядра атомов имеют собственный магнитный момент для магнитного момента атома, можно записать

, (3.8)

где z – порядковый номер атома в таблице Менделеева.

Соответственно для молекулы, состоящей из нескольких атомов, получим:

. (3.9)

Возможны такие случаи, когда в отсутствие магнитного поля

или . (3.10)

Надо отметить, что еще ранее (1909 г) Барнетт экспериментально установил, что при вращении магнетиков происходит их намагничивание. Этот эффект получил название механомагнитного.

Механомагнитный эффект, так же как и магнитомеханический эффект, доказывает, что молекулярные токи (микротоки), обуславливающие намагничивание, обладают механическим моментом.

О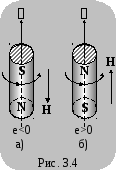пределяя знак возникающего намагничивания, можно установить и знак заряда движущихся частиц. Так, например, если частицы имеют отрицательный заряд, то магнитный и механический моменты каждого элементарного тока направлены противоположно, и поэтому магнитный момент тела и направление эквивалентного поля будут также противоположны угловой скорости вращения (рис. 3.4,а). Если же заряд частиц положительный, то магнитный момент тела и угловая скорость вращения должны быть направлены одинаково (рис. 3.4,б). Опыты показывают, что возникающее намагничивание соответствует отрицательному заряду частиц, и поэтому механомагнитный эффект так же, как и магнитомеханический эффект, подтверждают предположение о том, что намагничивание тел обусловлено движущимися электронами.

При наличии внешнего магнитного поля с индукцией B_o на электрон в атоме, кроме кулоновской силы, действует сила Лоренца F_л = evB_o. Так как плоскость орбиты электрона перпендикулярна B_o, то сила Лоренца в зависимости от направления движения электрона по орбите будет направлена либо к оси вращения, либо от нее. Тогда вместо равенства следует написать

. (3.11)

Следовательно, скорость v движения электрона по орбите при наличии магнитного поля должна отличаться от скорости v_o в отсутствие поля. Разность этих скоростей можно определить по формуле

или

. (3.12)

Изменение скорости электрона приведет к изменению магнитного момента электронной орбиты на

. (3.13)

Можно доказать, что при любом направлении вращения электрона вектор p направлен против вектора индукции B_o внешнего магнитного поля, следовательно, в векторной форме для каждой орбиты изменение магнитного момента

. (3.14)