6.5. Закон Джоуля-Ленца в дифференциальной и интегральной формах

Двигаясь под действием силы F = eE, электрон проводимости приобретает некоторую энергию

. (6.53)

Провзаимодействовав с ионом кристаллической решетки, он отдает ему эту энергию, которая выделяется в проводнике в виде тепла.

Если взаимодействие электрона проводимости с ионом кристаллической решетки происходило в течение времени t, то за это время в проводнике выделится в виде тепла энергия

, (6.54)

где – число взаимодействий электрона проводимости с ионом кристаллической решетки.

Так как

то

, (6.55)

где 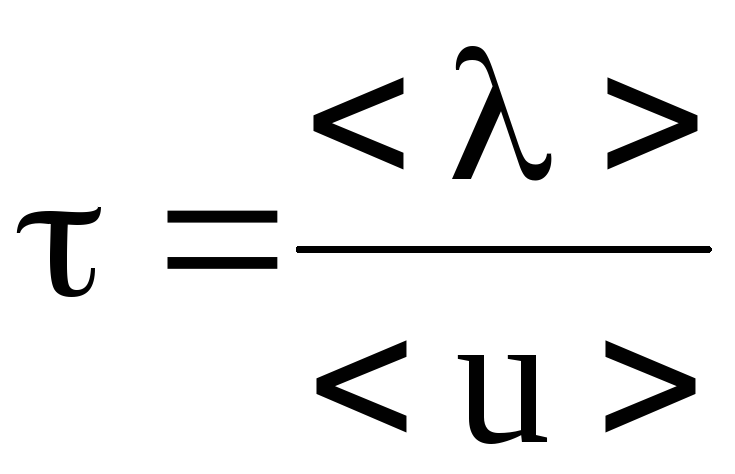– время свободного пробега электрона проводимости.

Если в объеме проводника содержится n электронов проводимости, то энергия, переданная единице объема проводника в единицу времени всеми электронами,

. (6.56)

Выражение (6.56) является математической формой записи закона Джоуля-Ленца в дифференциальной форме.

Из формулы (6.56) можно получить формулу закона Джоуля Ленца в интегральной форме. Имеем

,

где  = 1/; E = U/dl, dV = S dl.

Следовательно,

или

, (6.57)

где - сопротивление проводника;

U = IR – напряжение.

Количество тепла, выделившееся в проводнике за время t,

. (6.58)

Выражение (6.58) является математической формой записи закона Джоуля-Ленца в интегральной форме.

В случае постоянного тока

. (6.59)

Классическая электронная теория проводимости металлов смогла объяснить не только электропроводность металлов и сплавов, но и их теплопроводность, некоторые оптические свойства вещества, что является её крупным достижением. Однако с её помощью невозможно объяснить такие экспериментальные факты, как независимость теплоемкости металлов от наличия электронов проводимости и сверхпроводимости. Это связано с тем, что в ней электроны проводимости подчиняются законам идеального газа, законам статистики Максвелла-Больцмана. В действительности же для электронов проводимости справедлива квантовая статистика, и они подчиняются закону статистики Ферми-Дирака.

6.6. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (кпд) источника постоянного тока

На участке цепи, не содержащей ЭДС, силы электрического поля совершают работу по перемещению электрического заряда, которая выделяется в проводнике в виде тепла:

. (6.60)

Если в цепи имеется ЭДС, то работа по перемещению электрического заряда совершается сторонними и электрическими силами, численно равная энергии, выделяющейся в этой цепи:

. (6.61)

В замкнутой цепи энергия, выделяющаяся в проводнике численно равна работе:

. (6.62)

Таким образом, в замкнутой цепи внутри источника сторонние силы совершают работу по разделению зарядов, создают электрическое поле и запасают энергию, которая расходуется во внешней цепи на поддержание электрического поля, или выделяется в виде тепла. В замкнутой цепи совершают работу только сторонние силы.

Известно, что работа, совершаемая в единицу времени, называется мощностью:

. (6.63)

Это оказывается справедливым и для постоянного электрического тока. Поэтому для участка цепи, в котором отсутствует ЭДС, мощность

. (6.64)

При наличии ЭДС

. (6.65)

В замкнутой цепи

. (6.66)

Мощность во внешней цепи является полезной мощностью

. (6.67)

Отношение полезной мощности (мощности во внешней цепи) к мощности, развиваемой источником тока (полной мощности), называют коэффициентом полезного действия (КПД):

. (6.68)

Из выражения (6.67) видно, что при r0, 1.

Найдем соотношение между R и r, при котором полезная мощность максимальна. Для этого проведем исследование функции P_вн = f(R). Определяем первую производную и приравниваем её к нулю:

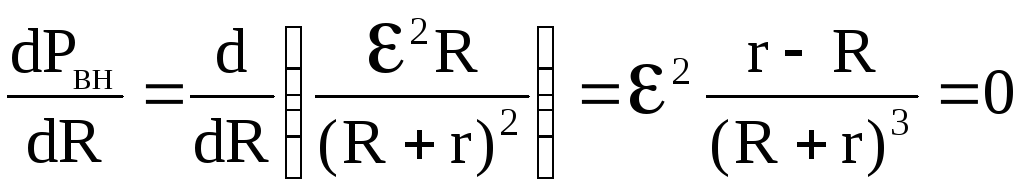. (6.69)

Определяем вторую производную и исследуем её знак:

. (6.70)

Из формул (6.64) и (6.65) видно, что в том случае, когда сопротивление внешнего участка цепи равно внутреннему сопротивлению источника тока (R = r), мощность во внешней цепи максимальна:

. (6.71)

При этом коэффициент полезного действия (при максимальном значении мощности во внешней цепи)

. (6.72)

Можно установить зависимость КПД источника тока от тока во внешней цепи ( = f (I)):

. (6.73)

Графики зависимости мощности во внешней цепи, полной мощности и коэффициента полезного действия источника тока от тока в цепи представлены на рис. 6. 12. Зависимость КПД от сопротивления внешнего участка цепи = f(R)

. (6.74)

Из вышеизложенного видно, что получение P_max и _max невозможно, т.к. при P_вн = P_max,  = 0,5, а при 1, P_вн0.