8.2.3. Длина дуги в полярных координатах

Пусть в полярных координатах задана кривая r=r() при . Разобьем кривую на достаточно малые части системой точек M_i. Соединим каждую пару соседних точек отрезком M_i-1M_i. В результате (см. рис. 5) в кривую впишется ломаная линия M₀M₁M₂...M_n. Обозначим длину отрезка M_i-1M_i через l_i. Проведем из начала координат дугу окружности лучом ОM_i до пересечения с лучом ОM_i-1 в точке N_i. Рассмотрим (см. рис. 7) треугольник M_i-1N_iM_i. С точностью до бесконечно малых он является прямоугольным. Катет M_iN_i =r_i_i; N_iM_i-1=r_i=r_i-r_i-1=r_i_i. Тогда по теореме Пифагора

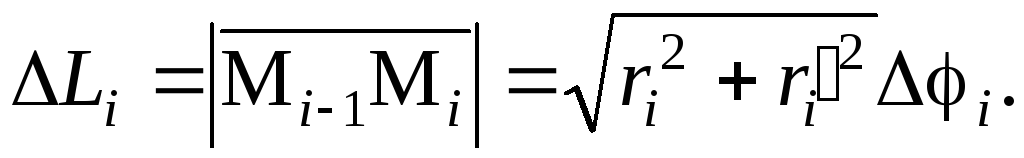
M_i

N_i

M_i-1

Рис. 7. Длина элемента дуги

Построим интегральную сумму и перейдем к пределу.

.

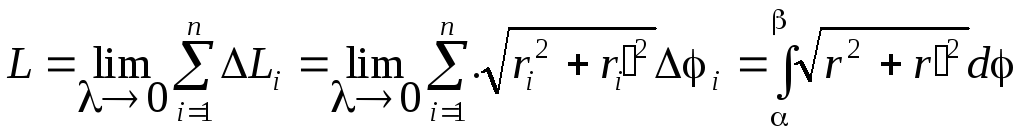Пример

Вычислить длину кривой r=2acos, 0. Кривая является окружностью диаметра 2a и, соответственно, радиуса a.

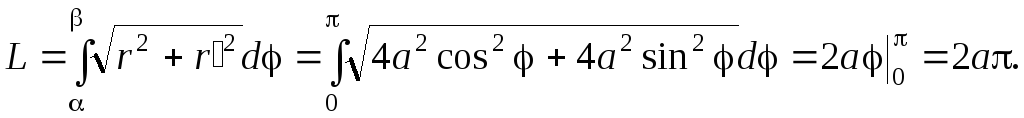
Мы получили формулу длины окружности.

8.3. Объем фигур

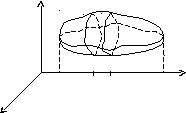
Пусть дана некоторая объемная фигура, объем которой нужно найти. Введем декартову систему координат Oxyz. Проведем через каждую точку оси Ox плоскость, перпендикулярную оси Ox. Рассмотрим площадь сечения фигуры плоскостью, проходящей через точку x на оси. Обозначим значение площади сечения через S(x). Это значит, что S(x) задает некоторую функцию от переменной x. Пусть крайние значения x, которые соответствуют левому и правому крайнему сечению фигуры, равны a и b. Разобьем интервал [a,b] на части системой точек a=x₀,x₁,x₂,...,x_n-1, x_n=b и проведем через каждую точку сечение. Обозначим S(x_i) площадь сечения, а также область, полученную при сечении. Проведем через каждую точку площади S(x_i) отрезок прямой, параллельный оси Ox, длины x_i до пересечения с площадью S(x_i-1). Образуется фигура, которую назовем элементарным цилиндром. Обозначим объем элементарного цилиндра V_i. Объем цилиндра равен:

V_i= S(x_i) x_i.

Просуммируем объемы элементарных цилиндров и перейдем к пределу (см. рис. 8). Получим:

z

O a x_i-1 x_i b x

y

Рис. 8. Вычисление объема с помощью сечений

Пример

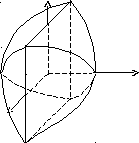
Вычислить объем тела, которое получается в результате перпендикулярного пересечения двух длинных круговых цилиндров одинакового радиуса, когда их оси вращения, тоже перпендикулярно пересекаются.

Выберем оси Oy и Oz, совпадающими с осями вращения, а ось Ox, перпендикулярную к ним. В плоскости Oxy получим уравнение кривой x²+y² =a². Сечение, параллельное плоскости Oyz, является квадратом. Откуда, сторона квадрата равна

z

O a x

y

Рис. 8. Вычисление объема с помощью сечений

Тогда площадь сечения и объем равны

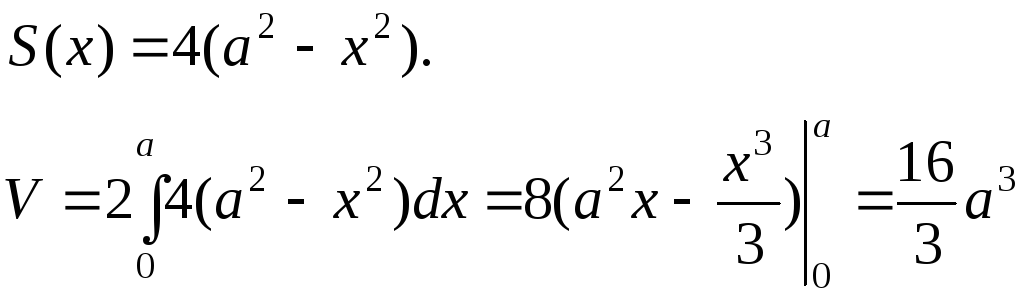
Пример

Вычислить объем, заключенный внутри эллипсоида

Положим x=h. Получим уравнение

Это уравнение эллипса с полуосями Площадь сечения равна

Объем эллипсоида равен

8.3. Объем и площадь поверхности тела вращения

Пусть на интервале [a,b] задана непрерывная функция y=f(x), причем f(x)0. Пусть кривая вращается вокруг оси Ox. Получится тело вращения. Разобьем интервал [a,b] на части системой точек a=x₀,x₁,x₂,...,x_n-1, x_n=b и проведем через каждую точку сечение. Обозначим S(x_i) площадь сечения, проходящей через точку x_i. Тогда площадь сечения и объем равны

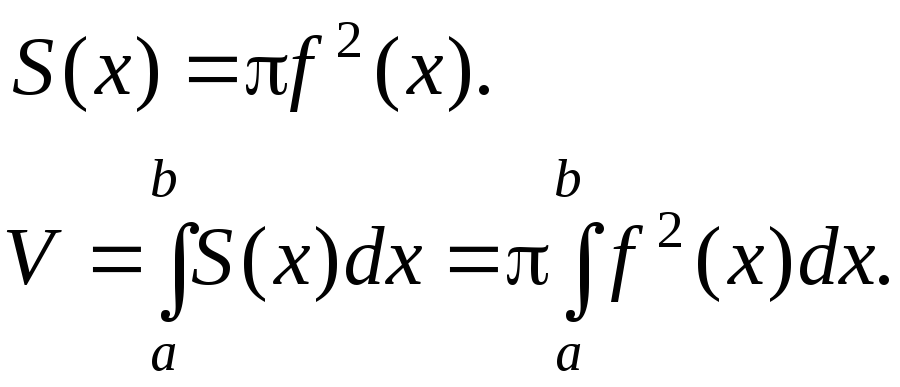
Проведем через точки (x_i,f( x_i)) ломаную линию. Площадь боковой поверхности тела вращения приближенно равна площади боковой поверхности тела, образованной вращением ломаной линии. Боковая поверхность элемента вращения ломаной равна

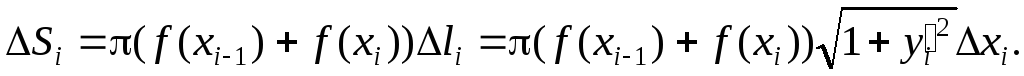
Площадь боковой поверхности тела вращения равна

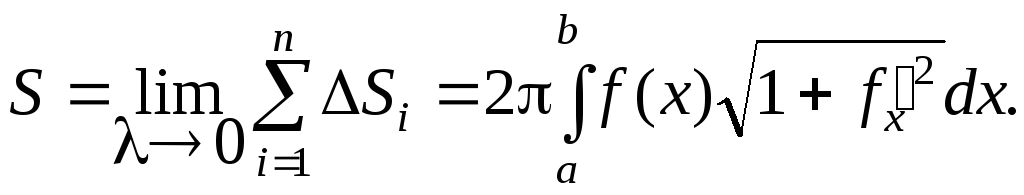
Пример

Вычислить объем и площадь боковой поверхности сферы

Сфера получается вращением вокруг оси Ox полуокружности , где a - радиус. Объем сферы равен

Найдем боковую поверхность.

Мы получили известные формулы объема и боковой поверхности шара.