1.3. Примеры выполнения задания 3

Данные задания могут быть решены методом замены переменной. При этом полезным будет вспомнить равенство

(или ), (1.10)

из которого вытекают следующие формулы:

(для ),

в частности:

Пример 3. Найти интегралы

а) ; б);

в) ; г);

д) ; е).

Решение.

а) сделаем замену переменной полагая . Найдем дифференциал от левой и правой части формулы:

или .

Окончательно,

и

Тогда

(см. табличный интеграл 5).

б) Заметим, что тогда обозначим

и применим формулу 2 из таблицы интегралов:

в) Для решения примера воспользуемся заменой

Тогда , т.е.откуда.

Итак,

г) Для решения данного примера воспользуемся равенством и заменой. Используя указанную замену и табличное интегрирование, получим результат:

д) Воспользуемся заменой, существенно упрощающей решение данного примера: . Тогда, откуда. Используя указанную замену и табличное интегрирование получим результат

е) Для решения примера воспользуемся заменой . Тогдат.е.и

Используя указанную замену и табличное интегрирование, получим результат

1.4. Примеры выполнения задания 4

Данные задания должны быть решены методом интегрирования по частям, т.е. с помощью формулы интегрирования по частям:

. (1.11)

В указанном равенстве произвольную постоянную мы не пишем, т.к. в правой части формулы остался неопределенный интеграл, содержащий произвольную постоянную.

Полезно запомнить следующие 6 типов интегралов, которые удобно вычислить интегрированием по частям (n-натуральное число, а  действительное число)

1. ; 2.;

3. ; 4.;

5. ; 6..

Для интегралов 1, 2, 3 следует принимать за u множитель , т.е. обозначить. Это приведет к интегралу сходного типа, но уменьшит степень х на единицу. После n-кратного применения этого приема мы получим один из табличных интегралов

, ,.

В интегралах 4, 5, 6, за u следует принять множитель при степенной функции, т.е. ,илисоответственно.

Пример 4. Найти интегралы, применяя метод интегрирования по частям

а) ; б);

в) ; г)

Решение.

а) Введем обозначения . Тогда

и . Применяя формулу интегрирования по частям (1.11) получаем

б) Обозначим .

Тогда

и .

Применяя формулу интегрирования по частям (1.11) получаем

в) Полагаем, что .

Тогда и

.

Применяя формулу (1.11) получаем

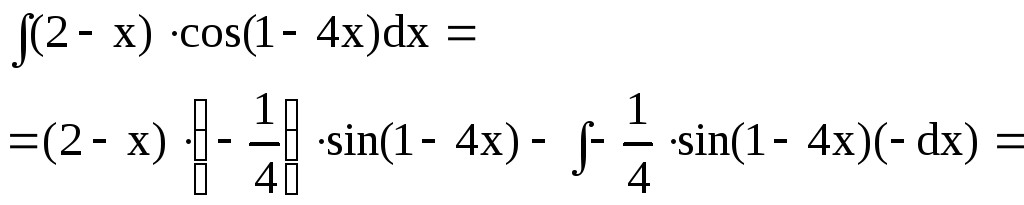
г) В данном примере для нахождения искомого интеграла формулу интегрирования по частям придется применять дважды.

Полагаем, что . Тогдаи. Применяя формулу интегрирования по частям, получаем

Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Действительно, обозначим теперь

Тогда ,и