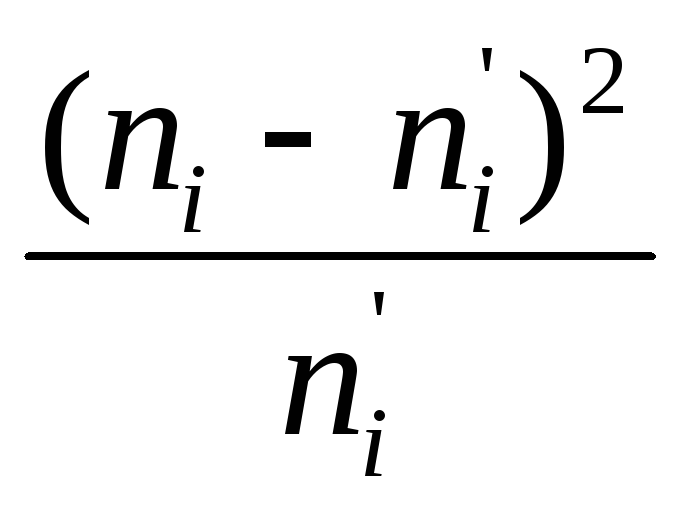Тема 12. Проверка статистических гипотез

Статистическая гипотеза, примеры гипотез. Нулевая (основная) и конкурирующая (альтернативная) гипотезы, простая и сложная гипотезы. Ошибки первого и второго рода, уровень значимости. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область и область принятия гипотезы. Критические точки. Левосторонняя и правосторонняя критические области, двусторонняя критическая область. Отыскание критических областей. Мощность критерия. Критерий согласия. Примеры критериев согласия. ² – распределение. Критерий «хи квадрат» (К.Пирсона). Проверка гипотез о распределении Пуассона и о нормальном распределении генеральной совокупности с помощью критерия согласия Пирсона. Методики вычисления теоретических частот распределения Пуассона и нормального распределения. Понятие о критерии Романовского.

Л и т е р а т у р а

[1], раздел 3, гл.9, раздел 4, гл.11; [3], гл.6, п.7.6; [4], §2; [5], гл.19, § 1-7, 22, 23, гл.17, § 5, 6; [8], гл.8, § 1-6; [9], гл.11, § 1-4; [11], гл.32, § 219; [12], ч.2, гл.5, § 20; [16], гл.6.

О с н о в н ы е п о л о ж е н и я и ф о р м у л ы

Распределение, плотность вероятности которого имеет вид

f(x) = (12.1)

называется «хи квадрат» распределением. Здесь Г(z) – гамма-функция, уже введенная в теме 10. Это распределение имеет один параметр k, называемый числом степеней свободы.

В критерии согласия «хи квадрат» (К.Пирсона) для проверки нулевой гипотезы используют случайную величину

² = . (12.2)

Здесь n_i – эмпирические (опытные) частоты, - теоретические частоты,s – число групп или частичных интервалов выборки. Случайная величина (12.2) характеризует близость эмпирического и теоретического распределений, так как содержит разности эмпирических и теоретических частот. Возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей частот.

Доказано, что случайная величина (12.2) при n имеет ²–распределение, т.е. ее плотность вероятности имеет вид (12.1). При этом число степеней свободы k=s-1-r, где r – число параметров предполагаемого теоретического распределения.

Если предполагают, что генеральная совокупность распределена по закону Пуассона (он содержит один параметр ), то r=1 и, следовательно,

k = s – 2. (12.3)

Если предположить распределение нормальным (оно имеет два параметра a и ), то r=2 и, следовательно, число степеней свободы

k = s - 3 (12.4)

Приведем правило проверки нулевой гипотезы (о предполагаемом законе теоретического распределения) с помощью критерия согласия Пирсона. Сначала вычисляются теоретические частоты. Затем находят наблюдаемое значение критерия ²_набл. по формуле (12.2). Далее, по таблице критических точек распределения ² при заданном уровне значимости  и по найденному числу степеней свободы (по формуле (12.3) для распределения Пуассона и по формуле (12.4) для нормального распределения) находят критическую точку ²_кр.(, k). Если ²_набл. <²_кр., то нет оснований отвергнуть нулевую гипотезу. Если же ²_набл. >²_кр, то нулевую гипотезу отвергают.

При применении критерия объем выборки должен быть значительным (обычно n>50). Малочисленные группы выборки объединяют с соседними, суммируя эмпирические частоты.

Теперь опишем способы нахождения теоретических частот.

В случае дискретного распределения признака Х генеральной совокупности теоретические (выравнивающие) частоты находят по формуле

= n P (X=x_i), (12.5) где n= n_i – число испытаний (объем выборки), P (X=x_i) – вероятность наблюдаемого значения х_i , вычисленная при допущении, что Х имеет предполагаемое распределение. Формула (12.5) следует из теоремы о математическом ожидании частоты появления события в независимых испытаниях.

Очень важным является дискретное распределение Пуассона. Тогда х_i принимает значения m: 0, 1, 2,… Вероятности P(X=x_i) из равенства (12.5) вычисляются по формуле Пуассона

Р(Х=m) = . (12.6)

Так как математическое ожидание этого распределения М(Х)=, а выборочная средняя является оценкой математического ожидания, то в формуле (12.6) за принимают .

В случае непрерывного распределения вероятности отдельных возможных значений равны нулю: Р(Х=х_i)=0. Поэтому весь промежуток возможных значений такой случайной величины разбивается на непересекающиеся интервалы (х_i, x_i+1) (обычно одинаковой длины h) и, естественно, вместо формулы (12.5) для вычисления теоретических частот применяют формулу

= n P (x_i  Х < x_i+1). (12.7)

Если F(х) – функция распределения случайной величины Х, то известно, что

P (x_i  Х < x_i+1) = F(х_i+1) – F(x_i). (12.8)

Если f(х) – плотность вероятности, причем непрерывная функция, то

P (x_i < Х < x_i+1) = , (12.9) где - некоторая фиксированная точка интервала (х_i, x_i+1). Обычно в качестве берут приближенное значение- середину интервала (х_i, x_i+1): .

Теперь рассмотрим важнейшее непрерывное распределение – нормальное. Исходя из (12.8) приходим к формуле

P (x_i < Х < x_i+1) = , (12.10) где Ф(х) – известная функция Лапласа, для нахождения значений которой имеются таблицы. Конечно, предварительно находятся иs.

Если же исходить из равенства (12.9), то в случае частичных интервалов одинаковой длины h(h= х_i+1 – x_i) и при =получим формулу

P (x_i < Х < x_i+1) = , (12.11) где(u) = - хорошо известная дифференциальная функция нормированного распределения (a=0, =1), которая уже табулирована. Множитель 1/s в формуле (12.11) естественным образом получается на основании замены u = . Параметры a и  заменены статистическими оценками иs.

При достаточно большом объеме выборки значение s в формулах (12.10) и (12.11) заменяется значением _В (см. тему 10).

Критерий согласия Романовского состоит в следующем. По формуле (12.2) вычисляется величина ². Затем находится значение выражения R = , где k – число степеней свободы. Если R>3, то выдвинутую гипотезу отвергают. Если R<3, то опытные данные согласуются с предполагаемыми теоретическими. Критерий удобен тем, что не нужно обращаться к таблицам критических точек.

Р е ш е н и е т и п о в ы х з а д а ч

Задача 1. На станке-автомате изготовлено за смену 1 000 графитовых стержней. Их распределение по весу (в граммах) задано таблицей:-

Вес в граммах	134- 137	137- 140	140- 143	143- 146	146- 149	149- 152	152- 155	155- 158	158- 161	161- 164	164- 167	167- 170	170- 173
Число стержней	1	4	16	53	121	193	229	186	121	53	17	5	1

Предполагая, что вес стержней подчиняется нормальному закону, найти теоретические частоты. Оценить с помощью критерия Пирсона, существенно ли расхождение между эмпирическими и теоретическими частотами при уровне значимости =0,05.

Решение. Вычислим характеристики эмпирического распределения:

Д_В =

Так как n=1000, то  заменяем величиной _В.

Вычислим теоретические частоты. Для расчетов используем формулы (12.7) и (12.10).

Все расчеты теоретических частот целесообразно свести в таблицу (характер вычислений указан в первой строке таблицы).

Вес Стержней в граммах (хi-xi+1)	Число стержней (ni)	хi-	xi+1-	Ф	Ф	Р(хi<X<xi+1)		Округ. Част.
		B	B
134-137 137-140 140-143 143-146] 146-149 149-152 152-155 155-158 158-161 161-164 164-167 167-170 170-173	1 4 16 53 121 193 229 186 121 53 17 5 1	-3,68 -3,11 -2,55 -1,98 -1,42 -0,85 -0,28 0,28 0,85 1,42 1,98 2,55 3,11	-3,11 -2,55 -1,98 -1,42 -0,85 -0,28 0,28 0,85 1,42 1,98 2,55 3,11 3,68	-0,999065 -0,494615 -0,47615 -0,422195 -0,30234 -0,11026 0,11026 0,30234 0,422195 0,47615ъ 0,494615 0,499065 0,499885	-0,499885 -0,499065 -0,494615 -0,47615 -0,422195 -0,30234 -0,11026 0,11026 0,30234 0,422195 0,47615 0,494615 0,499065	0,00082 0,00495 0,018965 0,053955 0,119855 0,19208 0,22052 0,19208 0,119855 0,053955 0,018465 0,00445 0,00082	0,82 4,45 18,965 53,955 119,85 192,08 220,52 192,08 119,85 53,955 18,465 4,45 0,82	1 4 19 54 120 192 221 192 120 54 18 4 1
	1000							1000

Для вычисления наблюдаемого значения критерия составим расчетную таблицу с объединением малочисленных групп:

Вес стержней в граммах (хi-xi+1)	Число стержней (ni)		ni -	(ni - )2
134-137 137-140 140-143 143-146 146-149 149-152 152-155 155-158 158-161 161-164 164-167 167-170 170-173	16 53 121 193 229 186 121 53 17	19 54 120 192 221 192 120 54 18	- -3 -1 1 1 8 -6 1 -1 -1 1	- 9 1 1 1 64 36 1 1 1 1	- 0,4737 0,0185 0,0083 0,0052 0,2896 0,1875 0,0083 0,0185 0,0556 0,20
					1,2652

Таким образом, ²_набл.=1,2 652. По формуле (12.4) найдем число степеней свободы, учитывая, что число групп выборки (после объединения) s=11. Следовательно, k=8.

По таблице критических точек распределения ² ([5], приложение 5) по уровню значимости =0,05 и числу степеней свободы k=8 находим ²_кр.(0,05; 8)=15,5.

Так как ²_набл.< ²_кр., то нет оснований отвергать нулевую гипотезу, т.е. данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Задача 2. Данные ЗАГСа в некотором районе за год по возрасту женщин, вступающих в брак, приведены в таблице:

Возраст невесты (хi)	19	20	21	22	23
Число невест (ni)	15	75	100	50	10

Проверить по критерию Пирсона при уровне значимости =0,01 согласованность полученных данных с гипотезой о нормальном распределении этого признака генеральной совокупности.

Решение. Вычислим характеристики эмпирического распределения:

Используя формулы (12.11), (12.7), (12.2), выполним соответствующие вычисления. Результаты сведем в таблицу (характер вычислений указан в первой строке таблицы).

i	xi	ni	ui=	(ui)		ni-	(ni-)2
1 2 3 4 5	19 20 21 22 23	15 75 100 50 10	-1,98 -0,92 0,15 1,22 2,28	0,0562 0,2613 0,3945 0,1895 0,0297	14,98 69,6 105,14 50,51 7,92	0,02 5,4 -5,14 -0,51 2,08	0,0004 29,16 26,4196 0,2601 4,3264	0,000027 0,418966 0,25128 0,005149 0,516263
		250			248,15			1,2217

Итак, ²_набл.=1,2217. Число степеней свободы k=5-3=2. Из [5] (приложение 5) по уровню значимости =0,01 и числу степеней свободы k=2 находим ²_кр.(0,01; 2)=9,2. Значение ²_набл<²_кр. Следовательно, гипотеза о нормальном распределении женщин по возрасту вступления в брак не противоречит данным ЗАГСа.

Задача 3. Распределение числа вызовов, поступающих на АТС, наблюдающееся через каждую минуту, дается в следующей таблице:

Число вызовов в 1 мин (m)	0	1	2	3	4	5	6	7
Число наблюдений (ni)	112	168	130	69	32	5	1	1

Предполагая, что число вызовов, поступающих на АТС в одну минуту, подчиняется закону Пуассона, найти теоретические частоты. Определить с помощью критерия Пирсона, существенно ли расхождение между эмпирическими и теоретическими численностями при уровне значимости =0,05.

Решение. Так как в законе Пуассона параметр  равен математическому ожиданию, а его оценкой является выборочная средняя, то =

Используя формулы (12.6), (12.5), (12.2), выполним соответствующие вычисления. Результаты сведем в таблицу (характер вычислений указан в первой строке таблицы).

m	ni	Pi			()2
0 1 2 3 4 5 6 7	112 168 130 69 32 5 1 1	0,213 0,32945 0,25466 0,1312377 0,0507233 0,01568366 0,004041156 0,0008925	110 171 132 68 26 8 2 1	2 -3 -2 1 6 -3 -1 -	4 9 4 1 36 9 1 -	0,03636 0,05263 0,0303 0,014706 1,384615 1,125 0,5 -
						3,143611

Получили ²_набл.=3,143611.

По формуле (12.3) находим, что число степеней свободы k=8-2=6. Используя таблицу критических точек распределения критерия Пирсона, по уровню значимости =0,05 находим ²_кр. (0,05; 6)=12,6.

Так как ²_набл < ²_кр., то можно считать, что гипотеза о согласии полученных данных с законом распределения Пуассона не опровергается.

З а д а ч и

1. Проверены 200 приборов на срок безотказной службы. По результатам проверки получен следующий статистический ряд:

Срок службы прибора в часах	0-150	50-150	100-150	150-200	200-250	250-300	300-350	350-400	400-450
Число приборов	1	7	24	30	71	31	21	13	2

Предполагая, что срок безотказной службы приборов подчиняется нормальному закону, найти теоретические частоты. Оценить с помощью критерия Пирсона, существенно ли расхождение между эмпирическими и теоретическими частотами при уровне значимости =0,01.

2. Дано эмпирическое распределение 100 рабочих по заработной плате:

Зарплата	180-190	190-200	200-210	210-220	220-230	230-240	240-250	250-260
Число рабочих	4	17	23	16	15	13	10	2

Проверить гипотезу о нормальном распределении зарплаты рабочих с помощью критерия Романовского.

3. На продукции, выпущенной токарным станком, изготавливающим валики, отобрано для анализа распределения 250 валиков. Получены следующие данные:

Диаметр валика в см	3,1	3,3	3,5	3,7	3,9	4,1	4,3	4,5	4,7	4,9
Число валиков	2	7	12	25	98	72	18	10	4	9

Определить с помощью критерия Пирсона, при уровне значимости =0,05, существенно ли расхождение между эмпирическими и теоретическими численностями.

4. Дано распределение числа мужских курток, проданных магазином в течение одного рабочего дня:

Размер куртки	44	46	48	50	52	54	56	58
Число проданных курток	2	6	12	35	32	21	12	5

Предполагая, что закон распределения нормальный, найти теоретические частоты и, применяя критерий Пирсона, определить, согласуются ли они с данными опыта (=0,01).

5. Радиоактивное вещество наблюдалось в течение равных промежутков времени. Для каждого из этих интервалов регистрировалось число частиц, попавших в счетчик. В таблице приведены числа n_i промежутков времени, в течение которых в счетчик попало ровно m частиц:

m	0	1	2	3	4	5	6	7	8	9	10 и более
ni	57	203	383	525	532	408	273	139	45	27	16

Проверить, используя критерий ², гипотезу о согласии полученных данных с законом распределения Пуассона (=0,025).

6. Отсчет по шкале измерительного прибора оценивается приблизительно в долях деления шкалы. Приведено 200 результатов отсчета последней цифры между соседними делениями шкалы:

Шифра	0	1	2	3	4	5	6	7	8	9
ni	35	16	15	17	18	18	12	15	28	26

Вероятность появления любой цифры р_i=0,1. С помощью критерия Пирсона, при уровне значимости =0,05, установить, согласуются ли данные с законом равномерного распределения.

Л и т е р а т у р а

1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных.- М.: Финансы и статистика, 1983.- 471 с.

2. Боровков А.А. Курс теории вероятностей.- М.: Наука, 1972. – 288 с.

3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969.- 576 с.

4. Власюк Н.А. Краткий курс математической статистики: Тексты лекций.- Хабаровск: Хабаровская государственная академия экономики и права, 1997. – 56 с.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1978. – 368 с.

6. Гнеденко Б.В. Курс теории вероятностей. – М.: Наука, 1988. – 448 с.

7. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. – М.: Наука, 1982.- 160 с.

8. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов, ч.2.- М.: Высшая школа, 1983.-320 с.

9. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1982. – 256 с.

10. Колмогоров А.Н. Основные понятия теории веротяностей. – М.: Наука, 1974. – 120 с.

11. Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика. – Минск: «Вышэйшая школа», 1976. – 720с.

12. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики.- М.: Высшая школа, 1972.-480 с.

13. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.2.-М.: Наука, 1970. – 576 с.

14. Тиунчик М.Ф. Случайные величины. – Хабаровск, ХИНХ, 1993. – 116 с.

15. Чистяков В.П. Курс теории вероятностей.-М.:Наука, 1982. – 255 с.

16. Эддоус М., Стэнсфилд Р. Методы принятия решений. – М.: Аудит, ЮНИТИ, 1997.-590 с.