3.11. Изменение коэффициента полезного действия

В первом приближении можно принять, что при изменении числа оборотов значения КПД остаются неизменными вдоль кривых пропорциональности. Однако опытным путем установлено, что величина КПД η меняется в соответствии с уравнением

,

где γ = 0,2…0,36,

отсюда .

Пример 5. Для условий предыдущего примера определить мощность на валу насоса при n₁=1000 об/мин и при n₂=790,6 об/мин; значение КПД при n = 1000 об/мин  = 0,79.

Решение. При n = 1000 об/мин .

При изменении числа оборотов уменьшится величина КПД. Примем значение γ = 0,3. .

Мощность при n = 790,6 об/мин.

Если нет возможности изменить число оборотов насоса (рис.26), то для подачи необходимого расхода 0,25 м³/с требуется поддерживать на насосе напор 33 м (точка В). В этом случае мощность на валу

Часовой перерасход электроэнергии 107,9-63,4=44,5кВт-ч.

3.12. Изменение характеристики насоса

при уменьшении диаметра рабочего колеса

Понизить напор и подачу центробежного насоса при том же числе оборотов можно, уменьшив диаметр рабочего колеса. Из уравнений пропорциональности следует, что для двух вариантов значений диаметра колеса D₁ и D₂ одного и того же насоса

.

При уменьшении диаметра ширина выходной щели не изменяется, т.е. в₁= в₂; при неизменном числе оборотов

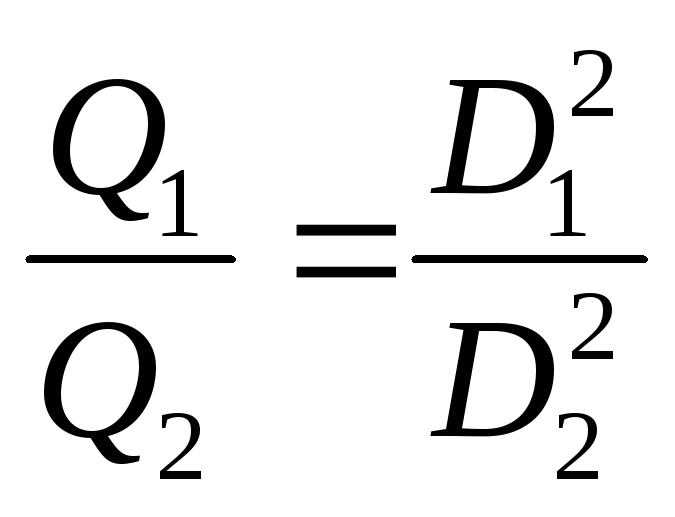. (16)

Опытным путем установлено, что такая зависимость справедлива для насосов с коэффициентом быстроходности n_s>150, при меньшем значении n_s более близкие результаты дает уравнение

.

Также из уравнения (12) следует, что

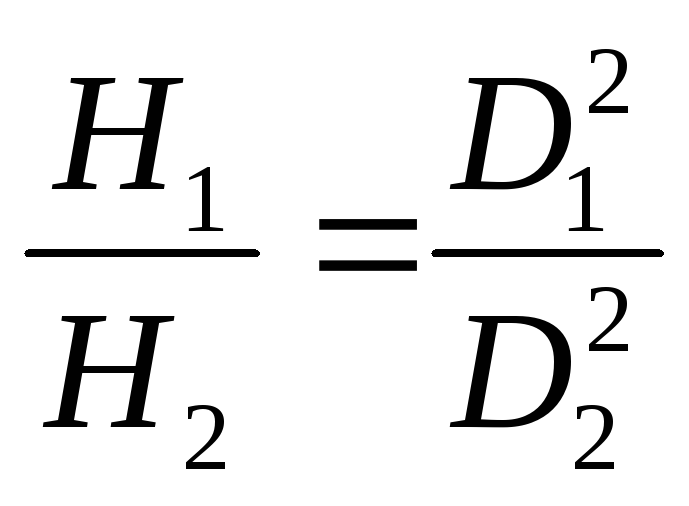, (17)

причем эта зависимость справедлива в широком диапазоне значений коэффициента быстроходности.

Для насосов с n_s>150 уравнения пересчета подачи и напора и аналогичны уравнениям пересчета при изменении числа оборотов, только вместоn₁ и n₂ подставляют значения D₁ и D₂.

Если при диаметре D₁ характеристика Q - H насоса

,

то при обточке рабочего колеса до диаметра D₂

.

Пример 6. Определить, до какого значения следует обточить диаметр рабочего колеса насоса, характеристика которого приведена на рис.27 , чтобы его подача и напор соответствовали значениям Q_А = 0,12 м³/с, Н = 30 м (точка А).Число оборотов – n =960 об/мин.

Решение. Определяем коэффициент быстроходности

.

Так как n_s<150, расчет ведем по формулам (16),(17). Проведем кривую пропорциональности через точку А по уравнению , при этом значениямQ 0,06; 0,1; 0,14; 0,16 м³/с соответствуют величины Н 7,5; 20,8; 40,8; 53,3 м.

П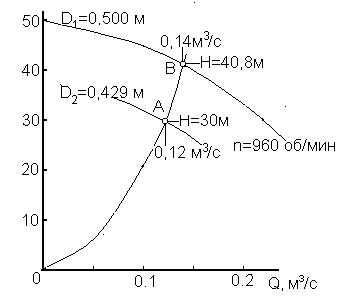ересечение кривой пропорциональности с характеристикой в точке В дает значения:

Q = 0,14 м³/с,

Н = 40,8 м.

Диаметр обточенного колеса определяем из уравнения (17):

Рис.27. Изменение характеристики при уменьшении диаметра рабочего колеса

м.

Процент обточки составляет

.

На графике (рис.28) максимальный допустимый процент обточки определяется заштрихованной зоной. В данном случае допустимая величина не превышена.

Рис.28. Допустимый процент обточки в зависимости от коэффициента быстроходности

Для насосов с коэффициентом быстроходности n_s>150 пересчет ведется по формулам:

и,

из которых следует, что и кривая пропорциональности превращается в прямую линию .

Если характеристика насоса при диаметре колеса D₁

, (18)

то при обточке этого колеса до D₂, заменив величины Q и Н на равные значения

и,

и подставив их в уравнение (18), получим:

.

Пример 7. Построить характеристику насоса с колесом, обточенным до диаметра 0,22 м, исходная характеристика которого при диаметре колеса 0,25 м приведена на рис.29.

Решение. Коэффициент быстроходности определяется для точки, расположенной в средней части рабочей зоны,

.

Воспользуемся для пересчета формулами (16),(17):

.

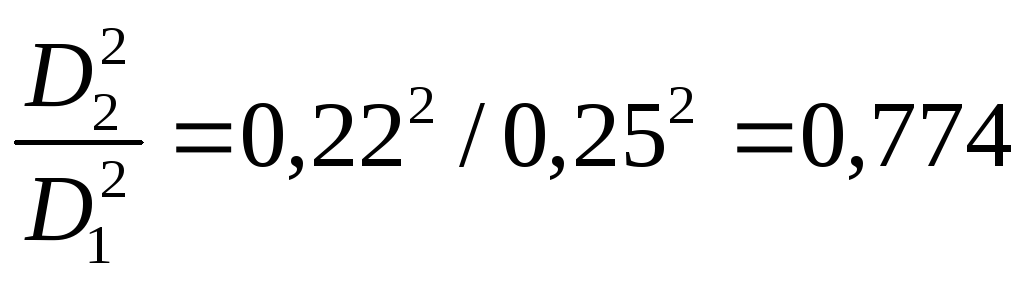Рис.29. Изменение диаметра рабочего колеса для насоса с коэффициентом быстроходности n_s>150

Для трех точек, взятых на исходной характеристике Q_A = 0,065;H_A = 24,5; Q_В = 0,11; Н_В = 22,0; Q_с = 0,16; Н_с = 16,2; находим точки, соответствующие диаметру обточенного колеса, для чего каждое из значений подачи и напора умножаем на 0,774:

Q_A1 = 0,050, H_A1 = 18,9; Q_В1 = 0,085, Н_В1 = 17,0;

Q_с1 = 0,123, Н_с1 = 12,4.

Как видно из рис.29, найденные точки лежат на прямых линиях, проведенных из начала координат через точки А, В, С. Процент обточки , не превышает допустимого (рис.28).

При обточке рабочего колеса происходит некоторое снижение коэффициента полезного действия.

Для расчета нового значения КПД пользуются формулой

,

где β≈0,45

или .