1.11. Метод двух узлов

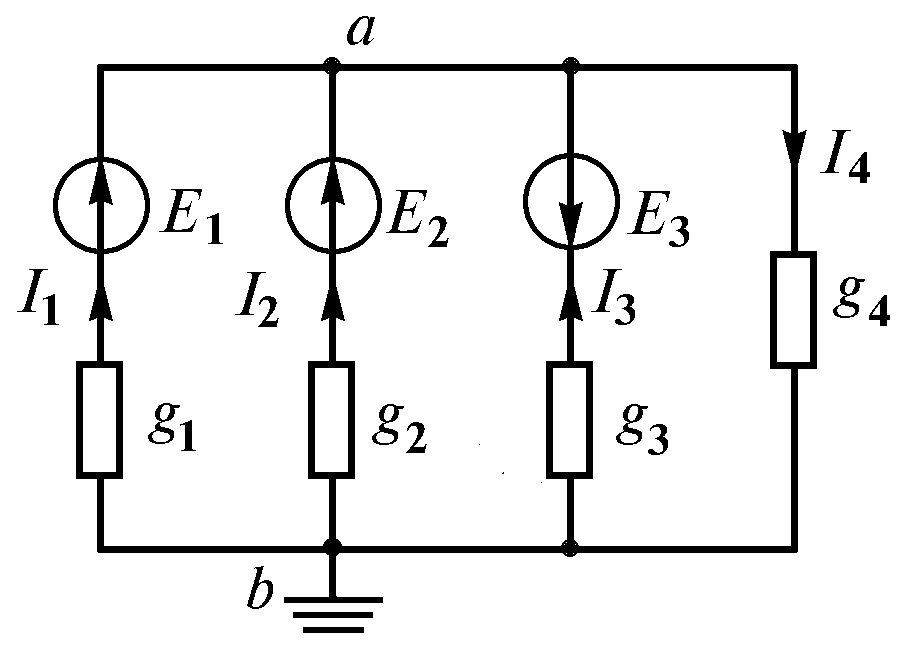
Под мето­дом двух узлов понимают метод расчета электрических цепей, в котором за искомое принимают узловое напряжение. С помощью напряжения между двумя узлами определяют токи в ветвях. На рис. 1.27 показана схема цепи с двумя узлами а и b, состоящая из четырех ветвей. Находим напряжение

Рис. 1.27

. (1.48)

В общем виде напряжение между двумя уз­ламинаходят по формуле

.

Произведение учитывается со знаком плюс, когданаправлено к узлу, потенциал которого условно принят за более положительный (к узлу с первым индексом).

Используя напряжение между узлами , по закону Ома определяем токи

Подставим эти уравнения в уравнение, составленное по первому закону Кирхгофа

,

Рис. 1.28

Три источника ЭДС, соединенные параллельно, можно заменить одним экви­валентным (рис. 1.28).

Из формулы (1.48) при = 0 имеем

В общем виде . (1.49)

Число элементов уравнения (1.49) определяется количеством ветвей, содержащих ЭДС. Учитывая , фор­мулу (1.49) запишем в виде

. (1.50)

Пример 1.3. Для схемы на рис. 1.27 определить ток , если= 25 В; = 30В; =15В;== 100Ом;= 200Ом;= 150Ом.

Решение. Напряжение между двумя узлами(1.48)

В.

Ток

А.

1.12. Принцип наложения

Принцип наложения представляет собой частный случай известного из фи­зики принципа независимости действия сил. Сущность принципа наложения за­ключается в том, что в любой ветви линейной цепи с постоянными сопротивле­ниями равен ток алгебраической сумме частичных токов, создаваемых в этой ветви каждой из ЭДС в отдельности. Таким образом, при определении токов в ветвях можно поочередно оставлять в схеме по одной ЭДС, считая, что все ос­тальные ЭДС равными нулю, но оставляя их внутренние сопротивления (рис. 1.29). Обычно получается цепь с последовательно-параллельным соединением сопротивлений. В этой цепи сначала определяются так называемые частичные токи, вызванные действием только первого источника ЭДС. Их обозначают и т.п. Таким же образом рассчитывают частичные токи (и т.д.), вызываемые действием второй ЭДС.

Алгебраически сложив частичные токи, определяют действительные значе­ния токов в каждом участке сложной цепи, когда все ЭДС действуют одно­временно.

Токи в ветвях .

Рис. 1.29

Порядок расчета по принципу наложения:

1) поочередно рассчитывают частичные токи, возникающие от действия каждого источника, мысленно удаляя остальные из схемы, но оставляя при этом их внутренние сопротивления;

2) определяют токи в ветвях алгебраическим сложением частичных токов.

Следует отметить, что принципом наложения нельзя пользоваться для рас­чета мощностей, так как мощность – квадратичная функция тока или напряже­ния. Например,

.

1.13. Метод эквивалентного генератора

При исследовании процессов в сложных электрических цепях часто появля­ется необходимость определить ток, напряжение и мощность только в од­ной ветви. В этом случае выделяют исследуемую ветвь, присоединенную к сложной цепи в двух точках. Остальная часть электрической схемы может быть условно представлена некоторыми прямоугольниками с двумя зажимами.

а) б) в)

Рис. 1.30

Часть электрической схемы произвольной конфигурации с двумя выде­ленными зажимами называетсядвухполюсником. Двухполюсники, содержащие источники электрической энергии, называютактивными. Если в двухполюсни­ках нет источников, их называютпассивными. В дальнейшем активные двухпо­люсники будем обозначать прямоугольниками с буквой А (рис. 1.30 б), а пас­сивные – прямоугольниками с буквой П (рис. 1.30 в). Всякий пассивный двухпо­люсник является потребителем электриче­ской энергии и характеризуется сопротив­лением, называемым внутренним или входным.

По отношению к выделенной ветви активный двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на выделенной ветви, а внутреннее сопротивле­ние равно входному сопротивлению пассивного двухполюсника.

Выделим в электрической цепи одну ветвь с сопротивлением , присоеди­ненную в точкахик активному двухполюснику (рис. 1.31 а). После замены активного двухполюсника эквивалентным генератором схема принимает вид, показанный на рис. 1.31 б.

Ток в выделенной ветви

, (1.51)

где – входное сопротивле­ние двухполюсника по отношению к зажимам.

Расчет по методу эквивалент­ного генератора сводится к сле­дующему:

а) находят напряжение на за­жимах разомкнутой ветви ;

б) определяют входное сопро­тивление всей схемы по отношению к зажимампри короткозамкнутых источ­никах ЭДС;

в) определяют ток по формуле (1.51).

При = 0 в цепи будет режим короткого замыкания. Ток короткого замы­кания определяют по формуле (1.51)

. (1.52)

Отсюда входное сопротивление

, (1.53)

то есть измеряют напряжение холостого хода на зажимах разомкнутой ветви и ток короткого замыканияветви.

Пример 1.4. Определить показание амперметра (ток) методом эквива­лентного генератора (рис. 1.32 а), если= 180В;= 100В;= 30Ом;= 40 Ом;60Ом;= 6Ом.

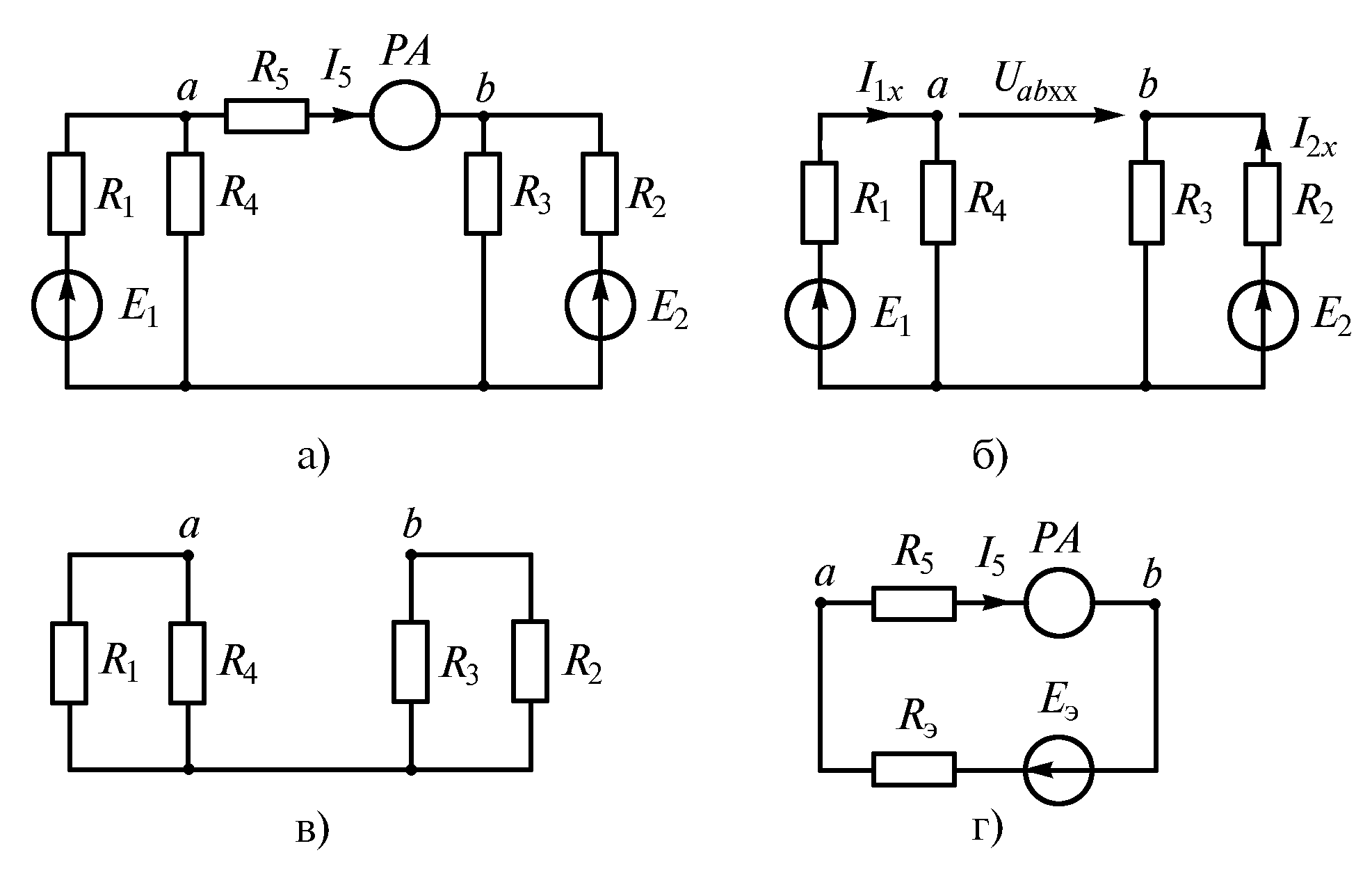
Рис. 1.32

Решение.

1. Разомкнем ветвь и найдем напряжение(рис. 1.32 б).

По закону Ома

А;А.

По второму закону Кирхгофа

.

Отсюда

E_э = U_{аb хх} = I_1х· R₄ – I_{2х ·}R₃ = 2 _· 60 – 1 _· 60 = 60 В.

2. Внутреннее сопротивление эквивалентного генератора равно входному сопротивлению пассивного двухполюсника. Источники ЭДС закорачиваем. Рас­четная схема для определения входного сопротивления показана на рис. 1.32 в.

Ом.

3. Окончательная расчетная схема (рис. 1.30 г) имеет вид одноконтурной цепи. В этой цепи ток

А.

32