1.8.3. Смешанное соединение резисторов

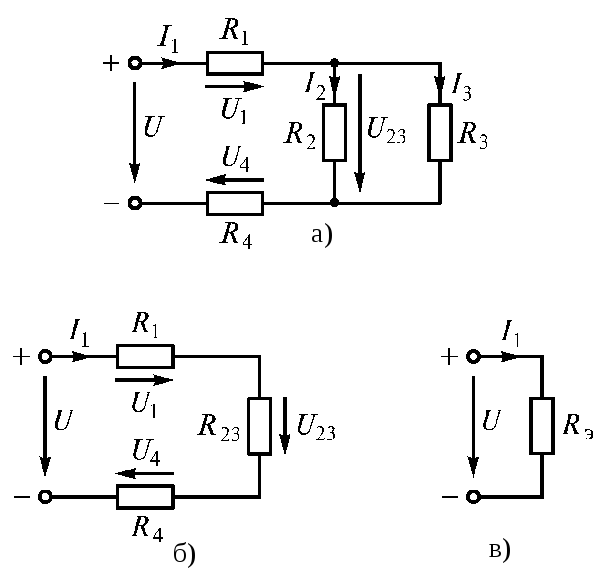
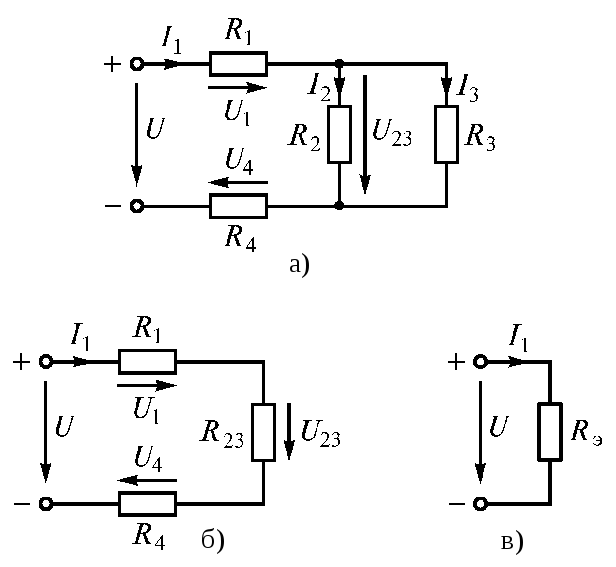
Смешаннымсоединением называют сочетание последовательного и парал­лельного соединений резисторов. Большое разнообразие этих соединений не позволяет вывести общую формулу для определения эквивалентного сопро­тивления цепи. Поэтому в каждом конкретном случае, используя методы расчета при последовательном и параллельном соединениях, можно рассчитать эквива­лентное сопротивление при смешанном соединении. Поясним это на конкретном примере расчета электрической цепи (рис. 1.20 а).

Электрическую цепь постепенно упрощают и приводят к простейшему виду (рис. 1.20 б, в)

;;;

.

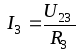Рис. 1.20

Проверка: 1)2).

1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот

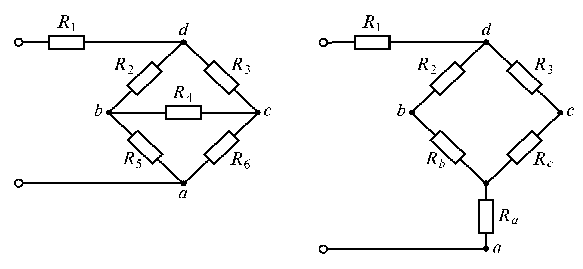
Рассмотрим две электрические цепи (рис. 1.21). Одна из них имеет вид тре­угольника, другая – трехлучевой звезды. В дальнейшем такие соединения будем называть соответственно соединением в треугольник и соединением звездой.

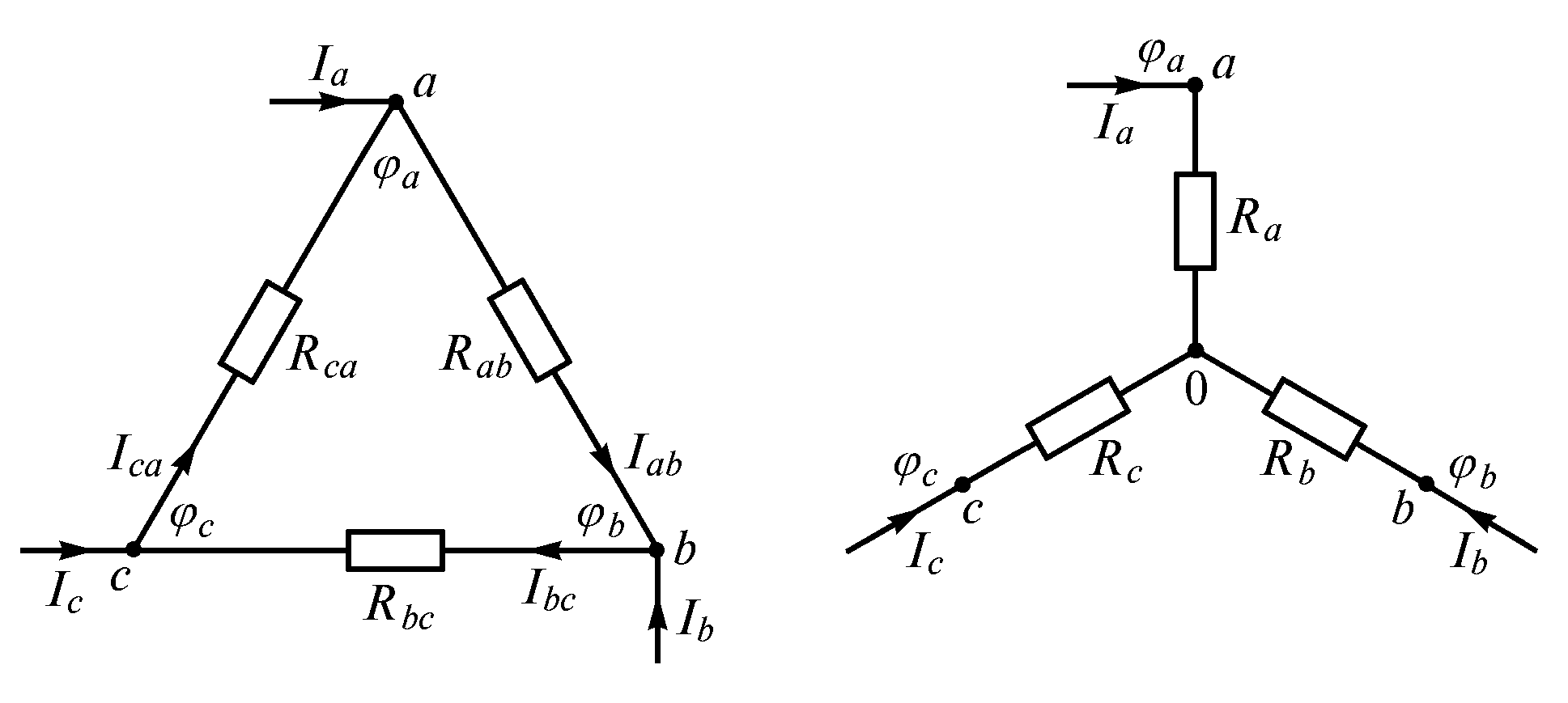
Рис. 1.21

Соединения такого вида очень распространены в трехфазных цепях, в кото­рых часто возникает необходимость перехода от одного вида соединения к другому (эквивалентному). Эквивалентность треугольника и звезды резисторов заключается в том, что их замена не изменяет потенциалов узловых точек (φ_а, φ_b иφ_с), являющихся вершинами треугольника и эквивалентной звезды. Не изме­няются также токи, напряжения и мощности в остальной части схемы, не затро­нутой преобразованием.

Формулы пересчета без вывода сопротивлений ветвей треугольника ,,в эквивалентную звезду,,имеют вид

(1.39)

При переходе от звезды к треугольнику можно воспользоваться следую­щими формулами

(1.40)

Если сопротивления всех ветвей цепи по схеме треугольник одинаковы, т.е. , сопротивления эквивалентной звезды будут также одина­ковые:, причем

.

1.8.5. Последовательное соединение источников энергии

В практике последовательное и согласное включение источников приме­няют для увеличения напряжения. Рассмотрим схему с двумя согласно и одним встречно включенными источниками (рис. 1.22).

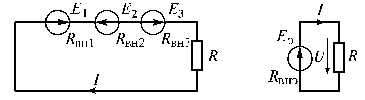
Рис. 1.22

По второму закону Кирхгофа запишем

. (1.41)

Отсюда

, (1.42)

где .

Напряжения на зажимах источников и приемника

.

При последовательном соединении источников с одинаковыми парамет­рами

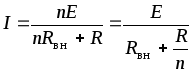. (1.43)

1.8.6. Параллельное соединение источников энергии

В тех случаях, когда номинальное напряжение приемника равно напряже­нию одного источника, а его ток больше допустимого тока одного источника, применяют параллельное соединение источников (рис. 1.23 а).

При параллельном соединении источников с одинаковыми параметрами их общая ЭДС не изменится, но уменьшатся токи через каждый источник и внутрен­нее сопротивление общего источника. Тогда эквивалентный источник (рис. 1.23 б) имеет следующие параметры: .

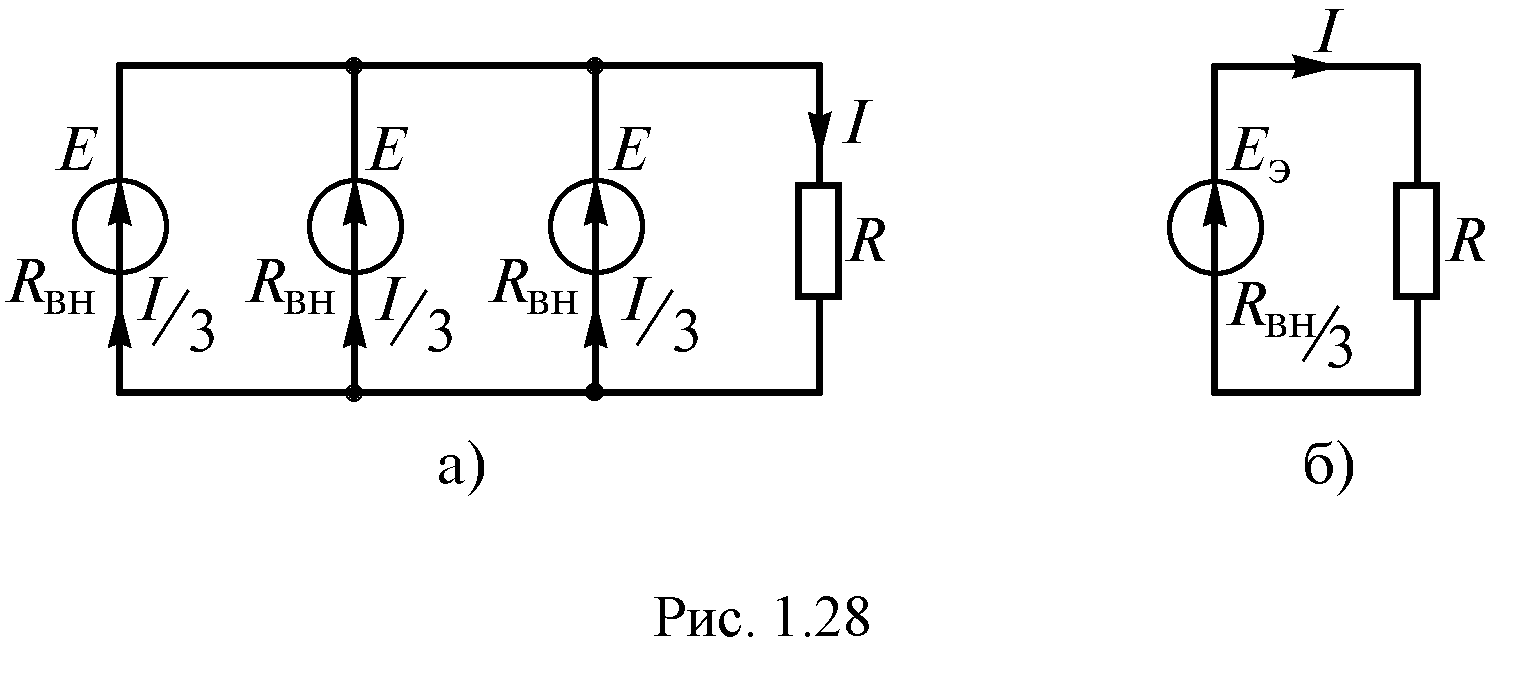
Рис. 1.23

Приисточниках

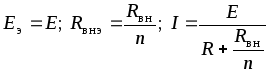. (1.44)

Пример 1.1. Определить эквивалентное сопротивление цепи (рис. 1.24 а), если 1Ом; 3Ом.

а) б)

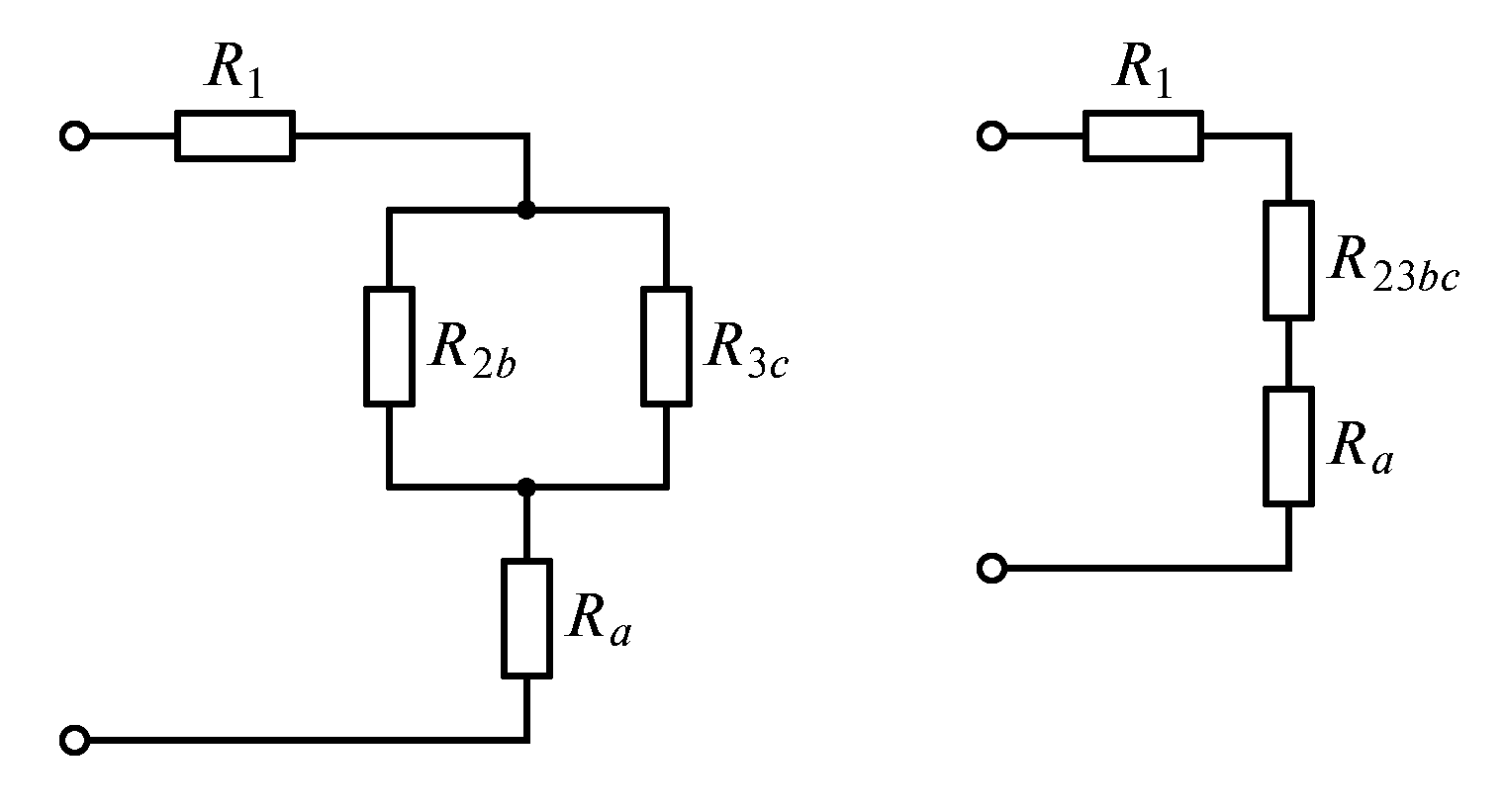
в) г)

Рис. 1.24

Решение. Преобразуем треугольник сопротивлений в эквивалент­ную звезду сопротивлений (рис. 1.24 б). Так как , то

Ом.

Дальнейшее решение выполним преобразованием последовательно или параллельно соединенных сопротивлений резисторов их эквивалентными сопротивлениями «свертыванием» схемы. Резисторы и, а такжеисоединены последовательно, поэтому их общие сопротивления

Ом;Ом.

Полученная схема приведена на рис. 1.24 в.

Резисторы исоединены параллельно, поэтому (рис. 1.24 г)

Ом.

Эквивалентное сопротивление всей цепи

Ом.

Пример 1.2.Определить токи в ветвях цепи (рис. 1.25 а), если задано:Ом;= 6Ом;Ом;= 2Ом;= 100В.

Решение. Резисторы исоединены последовательно и образуют ветвь с током. Резисторыивключены параллельно, а относительно резистора– последовательно. Вычислим эквивалентные сопротивления:

Ом;

Ом.

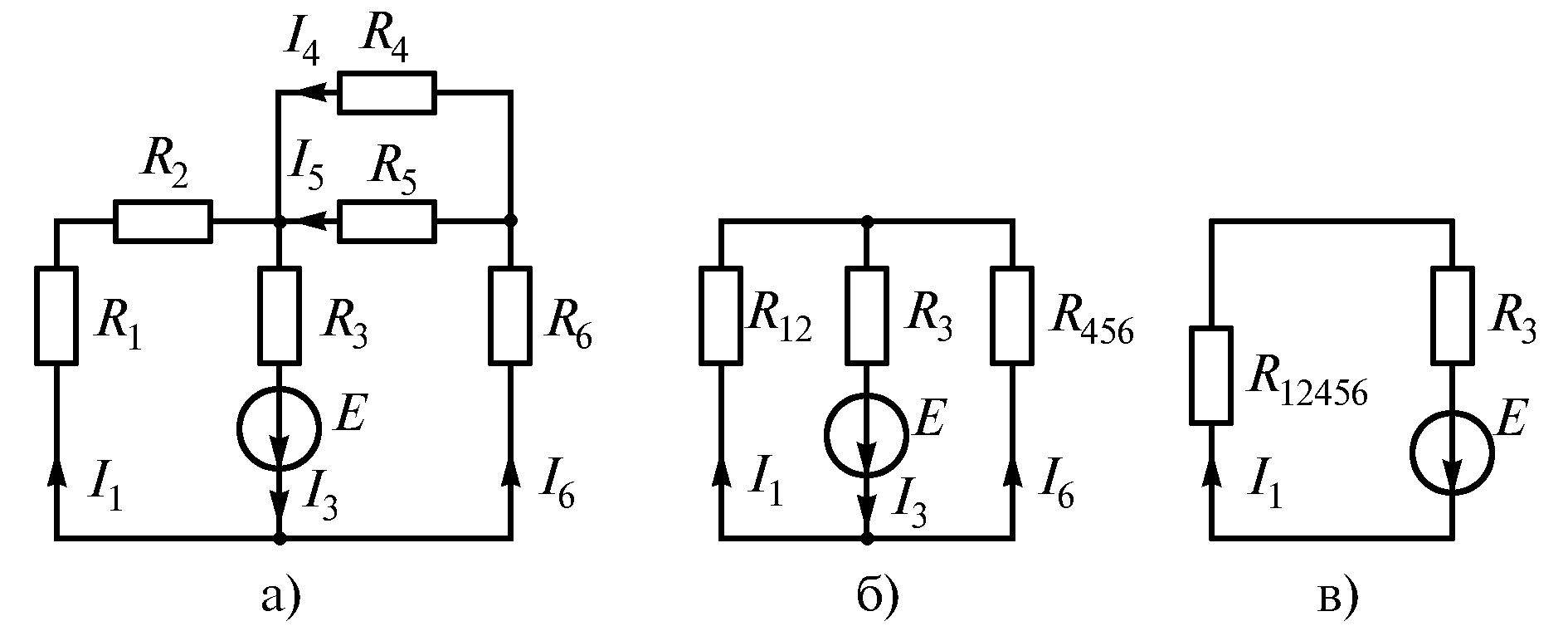
Рис. 1.25

Резисторы исоединены параллельно, а по отношению к– после­довательно, поэтому (рис. 1.25 б, в)

Ом.

Эквивалентное сопротивление цепи

Ом.

Ток в ветви с источником

А.

Так как сопротивления резисторов иодинаковы, то

А.

Аналогично, при

А.