
- •Курсовая работа
- •Содержание
- •Введение
- •1. Задание на курсовую работу
- •2. Составление структурной схемы радиотехнической системы
- •3.Определение вероятностных и числовых характеристик случайного сигнала
- •4. Определение корреляционной функции сигнала
- •5. Нелинейное преобразование сигналов.
- •Заключение
- •Список использованной литературы
3.Определение вероятностных и числовых характеристик случайного сигнала
В данной части задания требуется для заданной реализации эргодического сигнала u(t), вид которой представлен на рис. 1.1, определить:
а) Одномерную плотность распределения вероятностей мгновенных значений w(u);
б) Функцию распределения вероятности F(u);
в) Математическое ожидание, дисперсию и среднеквадратическое отклонение двумя способами:
- усреднением по множеству реализаций;
- усреднением по времени;
г) Вероятность того, что значения сигнала будут находиться в заданном интервале от U1 до U2.
Определение плотности распределения вероятностей
w(u)=
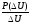 (3.1)
(3.1)
Найдем
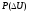 ,
т.е время пребывания (вероятность)
значений случайного напряжения Ui(t)
в интервале от U
до ( U+
,
т.е время пребывания (вероятность)
значений случайного напряжения Ui(t)
в интервале от U
до ( U+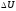 )
для различныхU.
)
для различныхU.

Рис 3.1 Реализация сигнала.
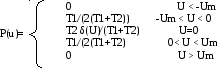
Видим, что ∑P(u)=1. (по свойству вероятности)
По формуле (3.1) находим одномерную плотность распределения вероятности.
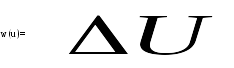
Зная
T1,T2
и
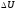 =|
Um|=1
вычислим одномерную плотность
распределения вероятности численно:
=|
Um|=1
вычислим одномерную плотность
распределения вероятности численно:
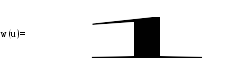

Описанные
выше соотношения должны удовлетворять
условию нормировки:
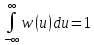 (3.2)
(3.2)
Одно из используемых свойств дельта функции:
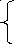
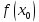 при
a
<
при
a
<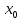 <
b
<
b
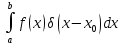 =
=
0
при
a
>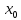 >
b(3.3)
>
b(3.3)
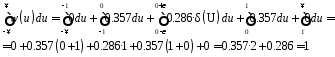
Удовлетворяет условию. Теперь строим график.
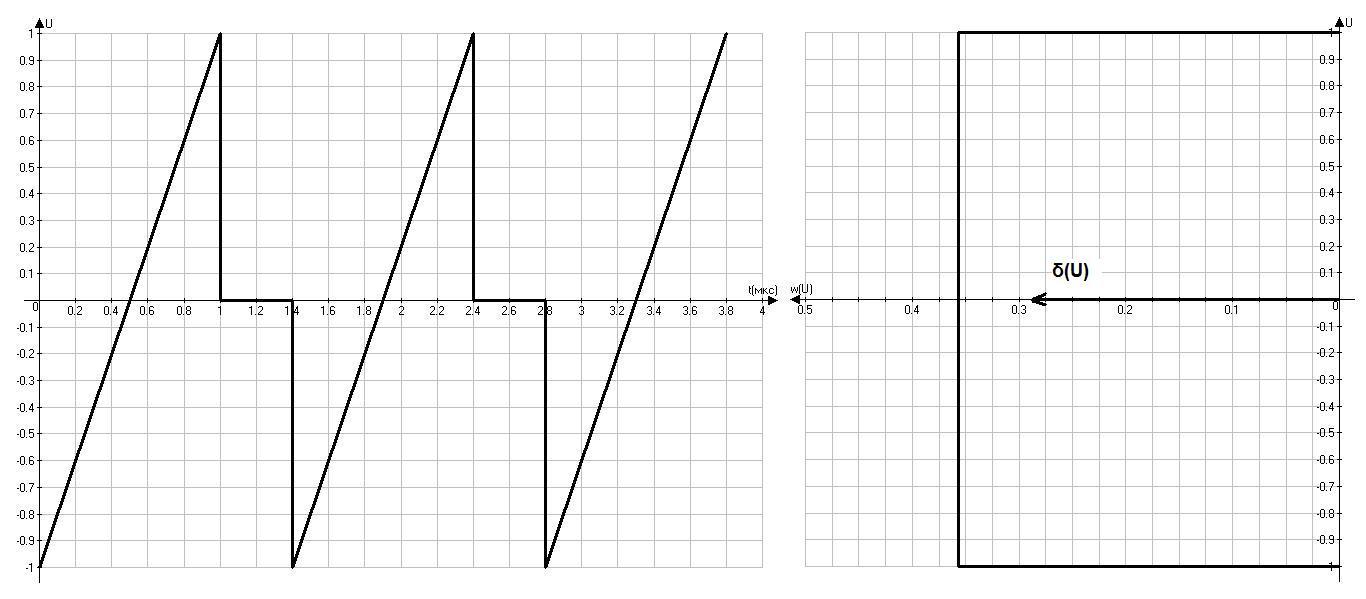
Рис 3.2 Реализация сигнала и его плотность распределения вероятности.
б) Определение функции распределения вероятностей
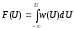 (3.4)
(3.4)
По формуле (3.4) и (3.3) определяем функцию распределения вероятности:
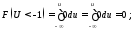
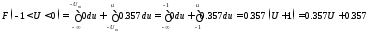

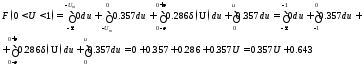
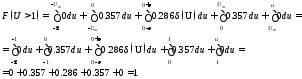
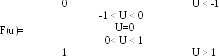
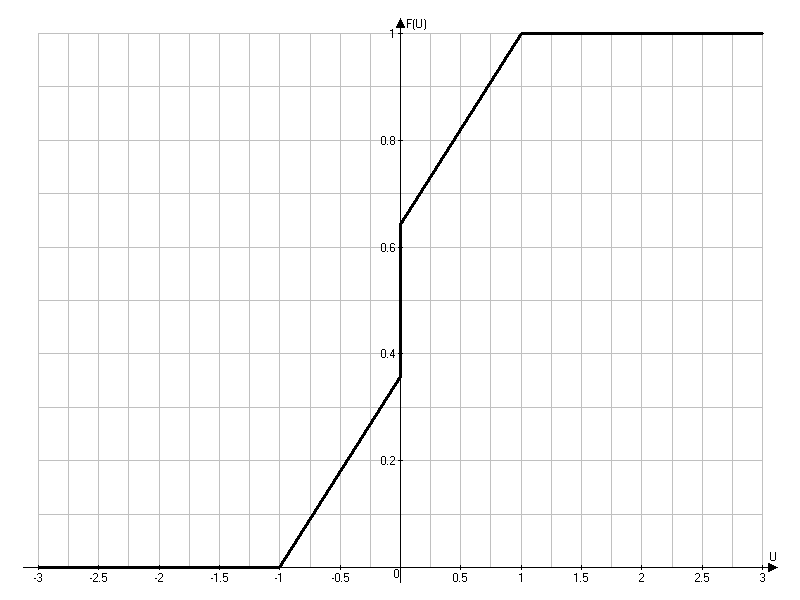
Рис 3.3 График функции распределения вероятности.
в) Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения.
Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения усреднением по множеству реализаций:
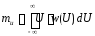 (3.5)
(3.5)
D
=
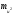 -(
-(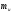 )2(3.6)
)2(3.6)
σ
=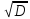 (3.7)
(3.7)
По формулам (3.5), (3.6), (3.7) а так же свойству (3.3) вычисляем математическое ожидание, дисперсию и среднеквадратическое отклонение.

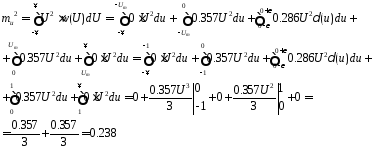
D=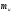 2-(
2-(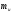 )2=0.238-02=0.238
В
)2=0.238-02=0.238
В
σ
=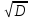 =
= =
0.488 В
=
0.488 В
Нахождение математического ожидания, дисперсии и среднеквадратическое отклонения усреднением по времени (процесс по условию эргодический):
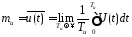 (3.8)
(3.8)
 (3.9)
(3.9)
σ
=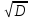 (3.10)
(3.10)
По формулам (3.8), (3.9), (3.10) вычисляем математическое ожидание, дисперсию и среднеквадратическое отклонение.
Tu=T1+T2=1+0.4=1.4
Функцию U(t) от 0 до T1 (прямая линия) найдем из уравнения прямой, проходящей через две точки: (u-u1)/(u2- u1)= (t-t1)/(t2- t1), где (u1, t1) и (u2, t2) координаты точек, соответственно равные (-1,0) и (1,1) см. рис 3.2
Отсюда U(t)=2t-1 от 0 до T1
U(t)=0 от T1 до T2

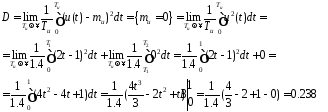
σ
=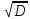 =
=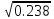 =
0.488 В
=
0.488 В
Напомним физический смысл математического ожидания, дисперсии и среднеквадратическое отклонения:
Математическое ожидание представляет собой среднее значение случайного процесса в текущий момент времени t. В нашем случае математическое ожидание равно нулю (реализации группируются по обе стороны от оси времени). Такой процесс называется центрированный. Физический смысл величины постоянная составляющая U.
Дисперсия характеризует разброс мгновенных значений реализаций случайного процесса относительно его среднего значения. Физический смысл мощность переменного составляющего случайного процесса.
Физический смысл среднеквадратическое отклонения – действующие значения напряжения или тока на единичном сопротивлении.
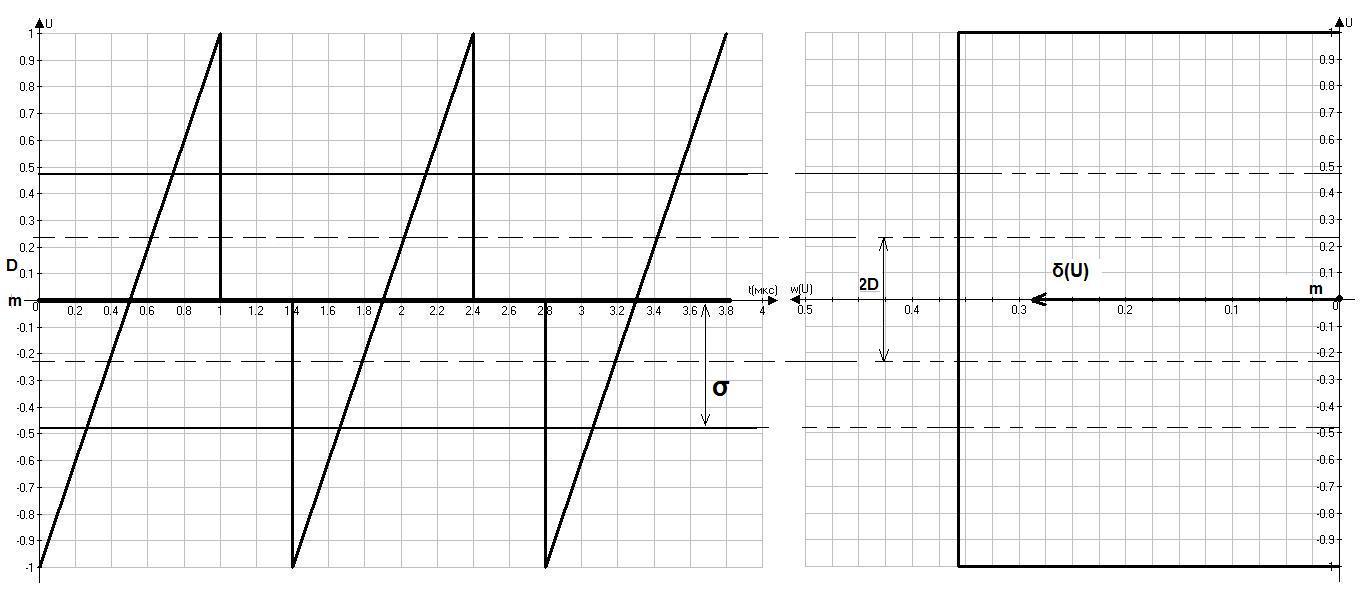
Рис 3.4 Математическое ожидание, дисперсия и среднеквадратическое отклонение на реализации сигнала и его плотности распределения вероятности
г) Определение вероятности того, что значения сигнала будут находиться в заданном интервале от U1 до U2.
Вероятность
попадания значений сигнала в заданный
интервал U1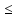 U
U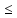 U2
U2
определяется через плотность распределения вероятности известным соотношением :
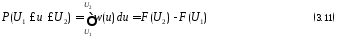
По
условию -0.5В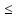 U
U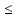 0.2В.
По формуле
(3.11) определяем вероятность:
0.2В.
По формуле
(3.11) определяем вероятность:
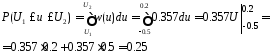

Рис 3.5 Вероятность того, что значения сигнала будут находиться в заданном интервале от U1 до U2
