
- •Тема 1: Спецификация эконометрической модели
- •1. Ошибки спецификации эконометрической модели имеют место вследствие …
- •2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
- •3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
- •4. В модели вида количество объясняющих переменных равно …
- •5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
- •Тема 2: Отбор факторов, включаемых в модель множественной регрессии
- •1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,иблизок к единице. Это означает, что факторы,и…
- •2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
- •3. Дана матрица парных коэффициентов корреляции.
- •4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами,иблизок к нулю. Это означает, что факторы,и…
- •Тема 3: Фиктивные переменные
- •1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
- •2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
- •4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
- •5. В эконометрике фиктивной переменной принято считать …
- •Тема 4: Линейное уравнение множественной регрессии
- •3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
- •Тема 5: Оценка параметров линейных уравнений регрессии
- •1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
- •2. Величина называется …
- •3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
- •4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
- •5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков.
- •Тема 6: Предпосылки мнк, методы их проверки
- •1. Для обнаружения автокорреляции в остатках используется …
- •4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
- •Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи мнк
- •2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
- •4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
- •Тема 9: Оценка тесноты связи
- •1. Для эконометрической модели вида показателем тесноты связи между переменнымииявляется парный коэффициент линейной …
- •2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
- •4. Для регрессионной модели вида получена диаграмма
- •Тема 10: Оценка качества подбора уравнения
- •1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
- •3. Для регрессионной модели вида , гдерассчитаны дисперсии:;;. Тогда величинахарактеризует долю …
- •Тема 11: Проверка статистической значимости эконометрической модели
- •Тема 12: Оценка значимости параметров эконометрической модели
- •Тема 13: Нелинейные зависимости в экономике
- •1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …
- •3. Нелинейное уравнение регрессии вида является _____ моделью ________ регрессии.
- •Тема 17: Временные ряды данных: характеристики и общие понятия
- •2. Дана автокорреляционная функция временного ряда
- •3. Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
- •4. Значение коэффициента автокорреляции второго порядка равно (-0,6), следовательно, ряд содержит …
- •5. Автокорреляцией уровней ряда называется корреляционная зависимость между …
- •Тема 19: Аддитивная и мультипликативная модели временных рядов
- •Тема 20: Модели стационарных и нестационарных временных рядов и их идентификация
- •1. Известно, что дисперсия временного ряда y увеличивается с течением времени. Значит, ряд y …
- •2. Известно, что временной ряд y порожден случайным процессом, который по своим характеристикам является «белым шумом». Значит, ряд y …
- •3. Известно, что временной ряд y характеризуется устойчивой тенденцией, то есть его среднее значение меняется. Значит, ряд y, скорее всего, является …
- •4. Для временного ряда известны характеристики: – среднее и– дисперсия. Если временной ряд является стационарным, то …
- •Тема 22: Классификация систем уравнений
- •1. При построении систем эконометрических уравнений различают три класса моделей:
- •2. Изучаются модели зависимости спроса и предложенияот ценыp и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений.
- •3. Установите соответствие между видом и классом эконометрических уравнений.
- •4. Установите соответствие между видом и классом системы эконометрических уравнений:
- •5. Установите соответствие между классом и видом системы эконометрических уравнений:
- •Тема 23: Идентификация систем эконометрических уравнений
- •1. Модель мультипликатора-акселератора Кейнса
- •2. Дана структурная форма модели системы одновременных уравнений:
- •3. Установите соответствие между структурной формой модели и приведенной формой модели
- •4. Установите соответствие между структурной формой модели и приведенной формой модели
- •Тема 24: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (кмнк) и двухшаговый метод наименьших квадратов (дмнк)
- •1. Если записать типы эконометрических моделей в следующем порядке:
- •2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
- •2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
- •2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
- •2. По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.
- •1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций рф в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций рф в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •1. Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •2. Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. Характеризуется данными, представленными на графике.
- •3. Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций рф в период 2005–2011 гг. Характеризуется данными, представленными на графике.
Тема 22: Классификация систем уравнений
1. При построении систем эконометрических уравнений различают три класса моделей:
(1) система независимых уравнений;
(2) система рекурсивных уравнений;
(3) система одновременных уравнений.
Отнесите предложенные модели к соответствующему классу.

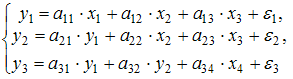


Решение:
Модель, в которой
![]() –
продуктивность коров, можно назвать
моделью экономической эффективности
сельскохозяйственного производства.
Эта модель содержит в правой части
только независимые переменные, поэтому
она может быть отнесена к классу «система
независимых уравнений».
–
продуктивность коров, можно назвать
моделью экономической эффективности
сельскохозяйственного производства.
Эта модель содержит в правой части
только независимые переменные, поэтому
она может быть отнесена к классу «система
независимых уравнений».
Модель, в которой
![]() –
производительность труда, может быть
названа моделью производительности
труда и фондоотдачи. Это модель содержит
в первом уравнении только независимые
переменные, а во втором уравнении в
правой части встречается и зависимая
переменная
–
производительность труда, может быть
названа моделью производительности
труда и фондоотдачи. Это модель содержит
в первом уравнении только независимые
переменные, а во втором уравнении в
правой части встречается и зависимая
переменная![]() ;
это значит, что модель можно отнести к
классу «система рекурсивных уравнений».
;
это значит, что модель можно отнести к
классу «система рекурсивных уравнений».
Модель, в которой
![]() –
темп изменения месячной заработной
платы, может служить моделью динамики
цены и заработной платы. В правых частях
обоих уравнений содержатся зависимые
переменные, поэтому данная модель может
быть отнесена к классу «система
одновременных уравнений».
Система, в
которойy
– объем производства, вообще не является
какой бы то ни было системой эконометрических
уравнений – это система нормальных
уравнений для определения параметров
парной линейной регрессии.
–
темп изменения месячной заработной
платы, может служить моделью динамики
цены и заработной платы. В правых частях
обоих уравнений содержатся зависимые
переменные, поэтому данная модель может
быть отнесена к классу «система
одновременных уравнений».
Система, в
которойy
– объем производства, вообще не является
какой бы то ни было системой эконометрических
уравнений – это система нормальных
уравнений для определения параметров
парной линейной регрессии.
2. Изучаются модели зависимости спроса и предложенияот ценыp и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений.
(1)
(2)

(3)

система независимых уравнений
система одновременных уравнений
система рекурсивных уравнений
система приведенных уравнений
Решение:
В системе (1) оба
уравнения зависят только от независимой
переменной p.
Это система независимых уравнений, и
мы не предполагаем, что спрос
![]() и
предложение
и
предложение![]() связаны
между собой.
связаны
между собой.
В системе (2)
зависимые переменные спрос
![]() и
предложение
и
предложение![]() содержатся
и в правой, и в левой частях уравнения.
Это система одновременных уравнений.
содержатся
и в правой, и в левой частях уравнения.
Это система одновременных уравнений.
В системе (3) первое
уравнение содержит в правой части только
независимую переменную p,
а второе уравнение уже включает в себя
и зависимую переменную
![]() ,
определенную в первом уравнении. Это
система рекурсивных уравнений.
,
определенную в первом уравнении. Это
система рекурсивных уравнений.
Система приведенных уравнений не является классом систем одновременных уравнений.
3. Установите соответствие между видом и классом эконометрических уравнений.
(1)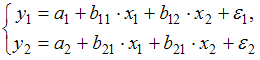
(2)
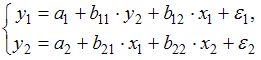
(3)
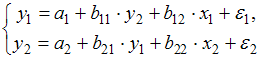
система независимых уравнений
система рекурсивных уравнений
система одновременных уравнений
система нормальных уравнений
Решение:
В системе (1) в обоих
уравнениях зависимые переменные
![]() и
и![]() зависят
только от независимых переменных
зависят
только от независимых переменных![]() и
и![]() .
Это система независимых уравнений.
.
Это система независимых уравнений.
В системе (2) второе
уравнение содержит в правой части только
независимые переменные
![]() и
и![]() ,
а первое уравнение для
,
а первое уравнение для![]() уже
включает в себя и зависимую переменную
уже
включает в себя и зависимую переменную![]() ,
определенную во втором уравнении. Это
система рекурсивных уравнений.
,
определенную во втором уравнении. Это
система рекурсивных уравнений.
В системе (3)
зависимые переменные
![]() и
и![]() содержатся
и в правой, и в левых частях уравнения.
Это система одновременных уравнений.
Система
нормальных уравнений не относится к
классу эконометрических уравнений.
содержатся
и в правой, и в левых частях уравнения.
Это система одновременных уравнений.
Система
нормальных уравнений не относится к
классу эконометрических уравнений.
