2.3. Расчет динамической погрешности

Переход в соседние состояния происходит тогда, когда реверсивный счетчик переходит из состояний - (S-1) или (S-1) в состояние "0". Поэтому система синхронизации описывается матрицей типа (7), где:

(2.8)

Таким образом, для расчета емкости реверсивного счетчика нужно задаться коэффициентом S, вычислить для него матрицы для всех состояний e₀, e ₁, ….. e_r и проверить затем выполнение неравенства :

, (2.9)

где: h- номер состояния при котором e _h = e _доп.

Минимальная статическая погрешность синхронизации

Так как для устойчивости корректирования должно выполняться условие

то принимаем, что

и .

Отсюда , а.

По условию , следовательно.

Полученная величина 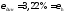по условию не должна превышаться с вероятностью 0,99.

Шаг коррекции . Это значит, что при переходе системы из состоянияe_i в состояние e_i-1 или e_i+1 разность фаз распределителей передачи и приема изменяется на 1,7 % длительности элементарной посылки.

Так как , то вероятность превышения величиныравна.

Динамическую погрешность, превышающую допустимую, можно положить равной e_r и считать, что вероятности появления больших величин динамической погрешности равны нулю.

Величину r найдем из формулы

.

Матрица переходных вероятностей для реверсивного счетчика емкостью S=3 имеет вид:

Составим систему уравнений для вероятностей состояний реверсивного счетчика:

Решая эту систему уравнений, и учитывая, что находим

(2.10)

Найдем переходные вероятности для реверсивного счетчика для различных величин рассогласований

По формулам (2.8) и (2.10) находим вероятности переходов для системы синхронизации, которые составляют матрицу переходов, записанную для абсолютных величин динамической погрешности.

Уравнения состояний системы синхронизации:

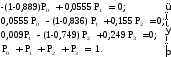
Решение системы уравнений:

Р₀ = 0,154; Р₁ = 0,308; Р₂ = 0,27; Р₃ = 0,262.

Проверка неравенства (2.9) показывает, что коэффициент деления делителя и емкость реверсивного счетчика выбраны правильно.

3. Исследование циклических кодов

1. Принципы построения циклического кода

Циклические коды – это (n;k)-коды, при которых цикл сдвигает кодовую комбинацию (КК) на 1 разряд вправо или влево, образуя комбинацию также принадлежащую коду.

n – длина КК;

k – число информационных символов;

–число избыточных (проверочных) символов,

. (3.1)

Получение КК путем циклического сдвига на 1 разряд аналогично аналитическому умножению многочлена навпервой степени. Умножение нахувеличивает КК на 1 разрад, чтобы избежать этого принимаем .

Признаком принадлежности КК к подмножеству разрешенных комбинаций является деление ее без остатка на произвольный (образующий) многочленстепенью. Если от деления есть остаток, то можно сделать вывод о том, что КК принята с ошибкой.

Существует 3 метода построения циклического кода. Рассмотрим каждый из них:

1. Метод умножения многочлена

Этот метод позволяет получить порождающую матрицу неразделимого кода (т.е. невозможно определить границу между информационными и проверочными символами).

Образующая матрица имеет вид:

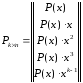, (3.2)

где 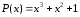- производящий (образующий) многочлен.

Все множество комбинаций кода получается из пяти строк матрицы и результатов суммирования по модулю два ее строк в любых сочетаниях. Также циклический код задается проверочной матрицей:

, (3.3)

; (3.4)

Проведем вычисления:

,

2. Метод деления многочлена

Получаемая КК находится по формуле:

(3.2)

где - информационный многочлен;

- остаток от деления _.

При этом КК не должна совпадать с КК.

.

_{В результате метода деления многочлена мы получаем разделимый код:}

_{1011 –информационная КК,}

_{100– проверочная КК.}