Разложение функции по формуле Тейлора

В Mathcad можно найти разложение функции по формуле Тейлора в окрестности любой точки из области определения функции. Сделать это можно через меню Символика (Symbolics) или с помощью Панели Ключевой Символики (Symbolic Keyword), которая открывается щелчком по кнопке в панели математических инструментов.

При работе через меню введите функцию, выделите переменную, щёлкните по строке Расширить в серии (Expand to Series) пункта Переменная (Variable) меню Символика (Symbolics), введите в окне диалога степень старшего члена в разложении и щёлкните по кнопке .

При работе с панелью символьных операций щёлкните сначала по свободному месту в рабочем документе, затем – по кнопке , введите перед ключевым словом series выражение для функции, а после ключевого слова – имя переменной и точку, в окрестности которой строится разложение, щёлкните в рабочем документе вне выделяющей рамки.

При работе с меню в рабочем документе отображается соответствующее разложение с остаточным членом в форме Пеано, при работе с панелью ключевых слов – только многочлен Тейлора (частичная сумма ряда Тейлора).

Пример 9.

Разложить функцию cos(x) по формуле Тейлора в окрестности нуля и в окрестности точки x=π/2.

Фрагмент рабочего документа Mathcad.

Лабораторная работа №1

Сходимость числовых последовательностей

Цель работы:

Нахождение предела числовых последовательностей.

Порядок выполнения работы:

1. Вспомнить основные операции нахождения предела последовательностей (см. Приложение А).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задание по номеру своего варианта.

Задание №1.1.

«Сходимость числовых последовательностей»

Найдите пределы последовательностей {a_n}, {b_n}, {c_n}. Для указанных значений ε = 10^-k найдите такие N(ε), чтобы все элементы последовательности с номерами n > N(ε) совпадали с предельным значением до k-го знака после запятой. Для заданных значений М укажите такие значения N(M), чтобы для всех членов бесконечно большой последовательности {c_n} с номерами n > N(М) выполнялось неравенство |c_n| > M. Изобразите графически сходящиеся последовательности и их пределы. Изобразите графически бесконечно большую последовательность. Варианты заданий в Таблице №1.1.

Порядок выполнения задания:

Исходная последовательность:

.

1. Установите режим автоматических вычислений.

2. Введите элемент последовательности {a_n} как функцию переменной n.

3. Используя символьную математику, найдите аналитически предел а последовательности {a_n}. Для этого в панели щёлкните кнопку , введите в помеченных позициях соответствующие символы, щёлкните кнопку панели Оценка и по рабочему документу вне выделяющей рамки:

4. Запишите уравнение для определения N(ε) и решите его, используя меню символьных операций. Запишите левую часть уравнения для вычисления N(ε), выделите n и щёлкните по строке Разрешить (Solve) в пункте Переменная (Variables) меню Символика (Symbolics). Скопируйте решение уравнения и присвойте его переменной N(ε).

Вычисление N(ε):

5. Для каждого заданного значения ε вычислите по полученной формуле значение N(ε):

6. Для любого n > N(ε), например для n = [N(ε)] + 1, вычислите |a_n – a_n| и сравните его с ε:

7. Выбрав достаточно большое значение N, вычислите значения элементов последовательности для n = 1, 2, …, N и изобразите на графике элементы последовательности как функции n. Изобразите на том же графике горизонтальные прямые y = a ± ε. Найдите на графике значение N(ε):

8. Выполните аналогичные вычисления для {b_n} и {c_n}.

Таблица №1.1

№	an	bn	cn	k	M
1				2	10
2				2	10
3				2	20
4				2	12
5				2	12
6				2	14
7				2	14
8				2	10
9				2	10
10				2	15
11				2	25
12				2	12
13				2	10
14				2	10
15				2	5
16				2	10
17				2	10
18				2	20
19				2	12
20				2	12
21				2	15
22				2	15
23				2	20
24				2	20
25				2	25
26				2	25
27				2	20
28				2	15
29				2	15
30				2	20

Контрольные вопросы:

1. Дайте определения числовой последовательности и её предела.

2. Какая последовательность называется сходящейся? Приведите пример.

3. Какая последовательность называется бесконечно малой и бесконечно большой? Приведите пример.

Лабораторная работа №2

Предел функции

Цель работы:

Нахождение предела функции в точке и сравнение бесконечно малых функций.

Порядок выполнения работы:

1. Вспомнить основные операции нахождения предела функции (см. Приложение В).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №2.1.

«Предел функции в точке»

Найдите предел функции f(x) в точке х = а. Для указанных значений ε = 10^-k найдите δ(ε) такие, что значения функции при 0 < |x - a|< δ совпадают с предельным значением до k-го знака после запятой. Изобразите графически поведение функции окрестности точки х = а. Варианты заданий в Таблице №2.1.

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений.

2. Определите (запишите) функцию:

3. Используя символьную математику пакета, найдите предел функции (см. Задание №1.1):

4. Запишите уравнение для определения δ(ε) и решите его, используя символьную математику (см. Задание №1.1):

5. Для каждого заданного значения ε вычислите по полученной формуле значение δ(ε):

6. Вычислите max |f(x) – A| и сравните его с ε.:

0<|x – a|<δ

7. Постройте график функции в окрестности точки х = а. Изобразите на том же графике горизонтальные прямые у = А ± ε. Найдите на графике значение δ(ε):

Таблица №2.1

№	f(x)	a	№	f(x)	a	№	f(x)	a
1		1	11		2	21		1
2		π/4	12		b	22		-1
3		4	13		2	23		2
4		1	14		2	24		2
5		-2	15		2	25		0
6		1	16		a	26		4
7		1	17		2	27		2
8		2π	18		1	28		2
9		-1	19		4	29		-1
10		π	20		2	30		2

Задание №2.2.

«Предел функции в точке»

Сравните бесконечные малые в нуле функции. Постройте графики функций в окрестности предельной точки. Варианты заданий в Таблице №2.2.

Порядок выполнения задания:

Исходные функции: , , , .

1. Установите режим автоматических вычислений.

2. Определите (запишите) все заданные функции:

3. Вычислите аналитически пределы функций в нуле, чтобы убедиться в том, что все заданные функции – бесконечно малые в указанной точке:

Вывод: все приведённые функции бесконечно малые.

4. Сравните заданные бесконечно малые функции, вычислив пределы их отношений в нуле:

f(x) = 0(p(x)) f(x) и p(x) бесконечно малые одного порядка малости

f(x) = 0(u(x)) f(x) более высокого порядка малости, чем u(x)

f(x) и w(x) несравнимы

Таблица №2.2

№	α(х)	β(х)	γ(х)	μ(х)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Контрольные вопросы:

1. Дайте определение пределу функции в точке.

2. Какая функция называется бесконечно большой? Приведите пример.

3. Какая функция называется бесконечно малой? Приведите пример.

4. По каким параметрам сравниваются бесконечно малые функции?

5. В каком случае бесконечно малые функции являются несравнимыми?

Лабораторная работа №3

Классификация точек разрыва.

Поведение функции на границах области определения

Цель работы:

Нахождение точек разрыва функции и исследование поведения функции на границах области определения.

Порядок выполнения работы:

1. Вспомнить классификацию точек разрыва и свойства непрерывных функций (см. Приложение С).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №3.1.

«Непрерывность и разрывы функций. Классификация разрывов»

Найдите точки разрыва заданных функций и определите их тип. Варианты заданий в Таблице №3.1.

Порядок выполнения задания:

Исходные функции: , , .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) выражение для функции:

3. Вычислите предел функции в точке разрыва:

4. Вычислите односторонние пределы функции:

5. Постройте график функции в окрестности точки разрыва:

6. Вывод: функция имеет разрыв в точке х = 0. Причём этот разрыв можно устранить, положив f(0) = 0, в результате чего получим непрерывную функцию.

7. Сформулируйте вывод и выполните вычисления для всех функций из заданных.

Таблица №3.1

№	f(x)	g(x)	h(x)	№	f(x)	g(x)	h(x)
1				16
2				17
3				18
4				19
5				20
6				21
7				22
8				23
9				24
10				25
11				26
12				27
13				28
14				29
15				30

Задание №3.2.

«Непрерывные функции. Свойства непрерывных функций»

Найдите (аналитически и графически) точки, в которых достигаются наибольшее и наименьшее значения заданной на отрезке непрерывной функции. Найдите нуль функции на заданном отрезке (решите уравнение f(x) = 0). Варианты заданий в Таблице №3.2.

Порядок выполнения задания:

Исходная функция: ; отрезок: [0, 1].

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) выражение для функции:

3. Постройте график функции:

4. Выберите на этом графике произвольный отрезок и найдите на этом отрезке наибольшее и наименьшее значения функции. Для этого щёлкните по полю графика, измените значения переменной х для отображения произвольного отрезка. Найдите наибольшее и наименьшее значения функции на выбранном отрезке:

5. Решите уравнение f(x) = 0, используя функцию root, выбрав в качестве нулевого приближения сначала левый, а потом правый конец заданного отрезка:

Таблица №3.2

№	f(x)	Отрезок	№	f(x)	Отрезок
1		[0,6]	16		[-2,4]
2		[1,4]	17		[-4,-1]
3		[1,4]	18		[-1,6]
4		[-3,3]	19		[-2,1]
5		[0,4]	20		[-1,7]
6		[-1,5]	21		[-1,5]
7		[1,9]	22		[1,9]
8		[0,3]	23		[-4,2]
9		[-3,3]	24		[-3,3]
10		[2,4]	25		[1,4]
11		[-1,2]	26		[-5,-2.8]
12		[-1,6]	27		[0,5]
13		[1,4]	28		[2,4]
14		[1,9]	29		[0,4]
15		[2,5]	30		[2,5]

Контрольные вопросы:

1. Какая функция называется непрерывной на промежутке?

2. Дайте определение пределу функции справа и пределу функции слева и запишите их обозначения.

3. Опишите условия, при которых функция может иметь разрыв.

4. Какой разрыв называется устранимым?

5. Что такое скачок функции в точке?

6. В чём заключается теорема Вейерштрасса?

7. В чём заключается теорема Больцано – Коши?

Лабораторная работа №4

Производная и её вычисление

Цель работы

Нахождение производных функций и вычисление значений производных в указанных точках.

Порядок выполнения работы:

1. Вспомнить определения производных, виды производных и основные методы нахождения их значений (см. Приложение D).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №4.1.

«Нахождение производной»

Найдите по определению производную функции f(x). Вычислите значение производной в указанной точке (в данном примере в точке х = 0). Варианты заданий в Таблице №4.1.

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите функцию:

3. Определите приращение функции в указанной точке. В нашем примере, поскольку f(0) = 0, то приращение функции ∆f(x) в точке х = 0 равно ∆f(0) = f(0 + ∆x) – f(0) = f(∆x).

4. Вычислите предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:

5. Вычислите производную аналитически. Для этого можно использовать меню символьных операций. Записав выражение дифференцируемой функции, выделите переменную х и щёлкните по строке Дифференцировать (Differentiate) в пункте Переменная (Variable) меню Символика (Symbolics). Можно использовать панель инструментов Исчисление (Calculus) математической панели инструментов. Щёлкните по кнопке , введите в помеченные позиции имя функции и переменной, выделите всё выражение и щёлкните :

Таблица №4.1

№	f(x)	№	f(x)	№	f(x)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Задание №4.2.

«Односторонние производные»

Вычислите производную функции f(x) по определению. Найдите значение производной функции в указанных точках. Вычислите по определению односторонние производные функции g(x) = |f(x)| в указанных точках. Постройте графики обеих функций и объясните различие поведения функций в окрестности указанной точки. Варианты заданий в Таблице №4.2.

Порядок выполнения задания:

Исходная функция: ; точки: х₀ = ± 2.

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Найдите производную от функции f(x) как предел отношения приращения функции к приращению аргумента:

3. Вычислите значения производной в указанных точках:

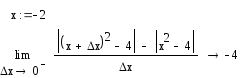
4. Попытайтесь так же найти производную функции g(x):

5. Вычислите по определению производную и односторонние производные функции g(x) в указанной точке. Сравните полученные значения:

6. Постройте графики функций f(x) и g(x):

Приведённые графики исследуемых функций подтверждают результаты вычислений: функция f(x) = x² – 4 – гладкая всюду, а функция g(x) = |x² – 4| теряет гладкость в точках х = ± 2.

Таблица №4.2

№	f(x)	№	f(x)	№	f(x)	№		f(x)
1		9		17		25
2		10		1		26
3		11		19		27
4		12		20		28
5		13		21		29
6		14		22		30
7		15		23
8		16		24

Задание №4.3.

«Геометрический смысл производной»

Для функции f(x) из Задания №4.2. покажите, что касательная, проходящая через точку (a, f(a)), − предельное положение секущей В данном примере для точки а = 1. Для функции g(x) = |f(x)| покажите, что у секущих, проходящих через точки (b, f(b)), (x₁, f(x₁)), x₁ > b, и (b, f(b)), (x₂, (f(x₂)), x₂ < b, − разные предельные положения. Варианты заданий в Таблице №4.2

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) функцию:

3. Найдите производную функции и вычислите её значение в точке х= 1:

4. Запишите уравнение касательной в точке х = а: y(x) = k(x – a) + f(a), k = f′(a):

5. Определите угловой коэффициент секущей k_s, проходящий через точки (x₀, f(x₀)), (x₁, f(x₁)), где х₀ = а, а х₁ = а − 1/n при n = 1:

6. Запишите уравнение секущей: y_s(x) = k_s(x – a) + f(a):

7. Постройте график функции f(x), а также касательную и секущую – графики функций y(x) и y_s(x):

8. Исследуйте поведение секущей, увеличивая значение n (при ; с изменением n на графике автоматически перерисуется секущая). Выполните построение для нескольких значений n. Приведём пример графиков функции f(x), касательной к нему и секущей, построенные для n = 1, 2,4 и 10 соответственно:

9. Выполните вычисления для пп. 4 – 7 для функции g(x). Секущие следует строить для и . Ниже приведён фрагмент рабочего листа Mathcad, в котором приведены все необходимые вычисления, график функции g(x), касательная к нему и секущая, построенные для n = 1, 2, 10 и 100 соответственно:

Приведённые выше графики объясняют геометрический смысл односторонних производных. Он заключается в следующем. Пусть непрерывная функция g(x) не имеет производной в точке х₀, но в этой точке определены односторонние производные g′₊(x₀) и g′₋(x₀). Тогда предельное положение секущей при x₁ → x₀, x₁ > x₀ (x₁ стремиться к х₀ справа) есть прямая с угловым коэффициентом, равным значению g′₊(x₀) правой производной функции g(x) в точке x₀. Эта прямая проходит через точку (x₀, g(x₀)) и пересекает график функции только в одной этой точке. Такую прямую можно назвать «правой касательной» к графику функции (на приведённых выше графиках она нарисована точечной линией синего цвета). Аналогично предельное положение секущей при x₁ → x₀, x₁ < x₀ (x₁ стремиться к х₀ слева) есть «левая касательная» к графику функции (на приведённых выше графиках она изображена пунктирной линией розового цвета).

Контрольные вопросы:

1. Дайте определение производной функции в точке, определённой на промежутке.

2. Каким образом определяется правая и левая производные функции в точке?

3. Объясните, в чём состоит геометрический смысл производной?

Лабораторная работа №5

Исследование функций и построение графиков

Цель работы

Исследование функций с помощью первой и второй производной и построение графиков.

Порядок выполнения работы:

1. Вспомнить основные положения относительно области определения функции для исследования характера поведения функции, а также методы нахождения точек экстремума (на графике первой производной) и точек перегиба (на графике второй производной) (см. Приложение E).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №5.1.

«Вертикальные и наклонные асимптоты»

Изобразите график заданной функции и подтвердите построение аналитическим исследованием: найдите координаты точек пересечения с координатными осями; найдите и постройте наклонные асимптоты. Запишите уравнения вертикальных асимптот. Варианты заданий в Таблице №5.1.

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) функцию f(x) и постройте её график:

3. Найдите точку пересечения с осью ординат, вычислив f(0). Сравните с данными на графике:

4. Найдите точку пересечения с осью абсцисс, решив уравнение f(x) = 0. Для этого необходимо записать выражение для функции, выделить переменную х, а затем использовать меню Символика, пункт Переменная, строка Разрешить. Сравните с данными на графике:

5. Найдите точки разрыва функции, вычислите соответствующие односторонние пределы, запишите уравнения вертикальных асимптот. Сравните с данными на графике:

6. Вычислите пределы и ; изобразите прямую y = kx + b:

7. Покажите, что равен нулю предел на бесконечности расстояния d от точки на кривой до наклонной асимптоты (d ≤ | f(x) − ( kx + b)| ):

Таблица №5.1.

№	f(x)	№	f(x)	№	f(x)	№	f(x)
1		9		17		25
2		10		18		26
3		11		19		27
4		12		20		28
5		13		21		29
6		14		22		30
7		15		23
8		16		24

Задание №5.2.

«Исследование функций с помощью производной»

Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график производной, найдите нули производной. Найдите координаты точек экстремума. Варианты заданий в Таблице №5.2.

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) функцию f(x) и найдите символически её производную:

3. Постройте графики функции f(x) и её производной:

4. Найдите нули производной. Для этого необходимо записать выражение для производной функции, выделить переменную х, а затем использовать меню Символика, пункт Переменная, строка Разрешить. Сравните с данными на графике:

5. Вычислите и запишите координаты точек экстремума. Укажите их тип (максимум / минимум):

Точка максимума (-1, -4)

Точка минимума (0, -5)

Таблица №5.2

№	f(x)	№	f(x)	№	f(x)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Задание №5.3.

«Исследование функций с использованием второй производной»

Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график второй производной, найдите нули второй производной. Найдите координаты точек перегиба. Варианты заданий в Таблице №5.3.

Порядок выполнения задания:

Исходная функция: .

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по вертикали.

2. Определите (запишите) функцию f(x) и найдите символически её первую производную:

3. Найдите символически вторую производную функции f(x):

4. Если возможно, упростите выражение для второй производной. Для этого запишите выражение для второй производной, выделите его полностью выделяющей рамкой, щёлкните по строке Упростить меню Символика:

5. Постройте график функции f(x) и её второй производной:

6. Найдите нули второй производной, решив уравнение f2 (x) = 0. Для этого необходимо записать выражение для второй производной функции, выделить переменную х, а затем использовать меню Символика, пункт Переменная, строка Разрешить. Сравните с данными на графике:

− нуль второй производной f2 (x)

7. Вычислите и запишите координаты точек перегиба:

− точка перегиба (1, -0.111)

На графике точка перегиба почти не видна. Однако аналитическое исследование − вычисление нуля второй производной, а также её график подтверждают, что функция имеет перегиб при х = 1. В рассмотренном случае удобно установить режим отображения результатов вычислений по вертикали.

Таблица №5.3

№	f(x)	№	f(x)	№	f(x)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Задание №5.4.

«Аналитическое исследование функции»

Постройте график функции и подтвердите изображение аналитическим исследованием. Варианты заданий в Таблице №5.4.

Порядок выполнения задания:

1. Установите режим автоматических вычислений.

2. Определите функцию и постройте её график.

3. Найдите наклонные асимптоты и изобразите их.

4. Постройте график первой производной и найдите точки экстремума.

5. Постройте график второй производной и найдите точки перегиба.

Фрагмент рабочего документа Mathcad с соответствующими вычислениями приведён ниже.

Наклонная асимптота: y = x + 1

Первая производная:

Упрощённый вид:

Решение уравнения f1 (x) = 0:

Точка максимума (-2, 1.587)

Вторая производная:

Упрощённый вид:

Решение уравнения f2 (x) = 0:

Точка перегиба (-3, 0)

В ходе вычислений громоздкие выражения для первой и второй производной были упрощены. Для этого необходимо выделить всё выражение и щёлкнуть по строке Упростить меню Символика. При исследовании перегибов найдите точки, в которых вторая производная не существует – это нули её знаменателя. Поскольку один их нулей знаменателя второй производной (х = 0) имеет кратность, равную двум, при переходе через него вторая производная не меняет знака. Функция имеет перегиб во второй точке (х = -3).

Таблица №5.4

№	f(x)	№	f(x)	№	f(x)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Контрольные вопросы:

1. Опишите условия, которые определяют характер поведения функции в области определения.

2. Каким образом можно исследовать поведение функции с помощью производной? Поясните на примере.

3. Каким образом можно исследовать поведение функции с помощью второй производной? Поясните на примере.

Лабораторная работа №6

Кривая на плоскости

Цель работы

Построение кривых на плоскости, заданных в декартовых координатах, в параметрической форме и в полярных координатах.

Порядок выполнения работы:

1. Вспомнить определение кривой на плоскости, а также уравнения касательных и нормалей к кривым, заданных в декартовых координатах, в параметрической форме и в полярных координатах (см. Приложение F).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №6.1..

«Кривые на плоскости, заданные в декартовых координатах»

Изобразите линии, заданные в декартовых координатах явно уравнением y = f(x) и неявно уравнением F(x, y) = 0. Запишите уравнения касательной и нормали к каждой кривой в указанных точках и изобразите их на графике. Варианты заданий в Таблице №6.1.

Порядок выполнения задания:

Исходные данные: цепная линия задана уравнением . Необходимо построить к ней касательную и нормаль в точке (1, ch1). Также необходимо построить эллипс и касательные и нормали к нему в точках (1, ± ).

1. Установите режим автоматических вычислений и режим отображения результатов символьных вычислений по горизонтали.

2. Определите (запишите) функцию f(x) и первую производную от неё:

3. Запишите уравнение касательной, проходящей через заданную точку, в виде, разрешённом относительно переменной y:

4. Запишите уравнение нормали, проходящей через заданную точку, в виде, разрешённом относительно переменной y:

5. Постройте график функции и изобразите на нём касательную и нормаль:

6. Введите левую часть уравнения, задающего линию в неявной форме, и разрешите его относительно переменной у. Для этого необходимо скопировать левую часть уравнения (выражение для F(x, y)) в рабочий документ, выделить переменную у, затем щёлкнуть по строке Разрешить в пункте Переменная меню Символика:

7. Определите функции, задающие явно части кривой, определённой в условии неявно:

8. Проверьте, лежат ли заданные точки и на кривой и не являются ли они особыми. Для этого необходимо сделать следующую подстановку:

Вычислим значения функций для двух заданных точек и сделаем проверку:

9. Запишите уравнения касательной и нормали в каждой из точек в виде, разрешённом относительно переменной у. Для этого необходимо сначала вычислить частные производные и :

Уравнения касательных и нормалей:

10. Постройте графики функций, определённых в п.7. Изобразите на тех же графиках касательные и нормали к ним:

Таблица №6.1

№	f(x)	x0	F(x, y)	(x0, y0)
1		1
2		2
3		1
4		-1
5		2
6		-2
7		1
8		-5
9		5
10		0,5
11		-1
12		-1
13		1
14		3
15		-3
16		-8
17		3
18		-3
19		10
20		-10
21		1
22		-1
23		3
24		-1
25		-3
26		3
27		1
28		0,5
29		1,5
30		-3

Задание №6.2..

«Кривые на плоскости, заданные в параметрической форме»

Изобразите на плоскости кривую, заданную параметрически, и касательную и нормаль к ней в указанной точке. Варианты заданий в Таблице №6.2.

Порядок выполнения задания:

Для значений λ, равных 1, 0.5, 2, постройте циклоиды , , , а также касательные и нормали к ним в точке .

1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) функции, задающие кривую параметрически (λ = 1):

3. Найдите аналитически (символьно) производные обеих функций:

4. Запишите уравнения касательной и нормали в точках в виде функций переменной х:

5. Постройте график функции и изобразите на нём касательную и нормаль. Для того чтобы построить график функции, заданной параметрически, введите в позиции, указанной меткой возле оси абсцисс, функцию, задающую значения аргумента (в рассматриваемом случае это φ(y)), в позиции возле оси ординат – функцию, определяющую аргумент (в рассматриваемом случае это ψ(х)). Чтобы построить на том же графике функции переменной х, введите в позиции для функции (через запятую) имена функции переменной х, а в позиции для аргумента, через запятую, - имя аргумента х:

В приведённом фрагменте вычисления организованы таким образом, что для исследования циклоиды с другим значением параметра λ достаточно изменить значение параметра в правой части оператора присваиваивания в превой строке рабочего документа. Ниже приведены изображения циклоиды для λ = 0.5 и λ = 2 соответственно:

Таблица №6.2

№	x(t)	y(t)	(x0, y0)	№	x(t)	y(t)	(x0, y0)
1			(1, 1)	16		2cos(t)sin(t)+ sin(t)
2			(1, -1)	17
3				18
4				19
5				20			(-1, 2)
6				21
7		cos(t)sin(t)+ +sin(t)		22	3
8				23
9				24
10			(1, 2)	25			(1, -2)
11			(1, -2)	26			(1, 1)
12				27
13				28
14				29
15				30

Задание №6.3.

«Кривые на плоскости, заданные в полярных координатах»

Изобразите кривую, заданную в полярных координатах. Варианты заданий в Таблице №6.3.

Порядок выполнения задания:

Исходная функция: .

1. Определите (запишите) функцию: .

2. Изобразите в полярных координатах график функции, используя кнопку в панели инструментов графиков. В открывшемся окне введите слева имя функции, внизу имя аргумента:

Таблице №6.3

№	r(φ)	№	r(φ)	№	r(φ)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Контрольные вопросы:

1. Дайте определение кривой на плоскости, заданной в декартовых координатах. Запишите уравнения, задающие такую кривую.

2. Какая кривая называется гладкой? Запишите уравнение касательной и нормали к такой кривой.

3. Запишите уравнения, задающие кривую в параметрической форме.

4. Запишите соотношения, которые связывают декартовы координаты с полярными.

Лабораторная работа №7

Формула Тейлора

Цель работы

Исследование формул Тейлора для заданных функций; построение графиков в окрестностях заданных точек.

Порядок выполнения работы:

1. Вспомнить формулы Тейлора для основных элементарных функций (см. Приложение G).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №7.1.

Запишите формулу Тейлора заданной функции. Исследуйте аналитически зависимость погрешности приближённой формулы Тейлора от степени многочлена и от расстояния |x – x₀|. Исследуйте поведение остаточного члена формулы Тейлора. Варианты заданий в Таблице №6.1 (Лабораторная работа №6).

Порядок выполнения задания:

Исследуем формулу Тейлора для функции sin(х) в окрестности нуля: .

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) функцию f(x):

3. Запишите разложение функции по формуле Тейлора в окрестности нуля. Для этого введите функцию (sin(x)), выделите переменную х, щёлкните по строке Расширить в серии в пункте Переменная меню Символика и укажите в окне диалога порядок остаточного члена:

4. Определите многочлены Тейлора как функции переменной х и скопируйте в них нужное число слагаемых из вычисленных выражений.

5. Постройте график функции многочленов Тейлора:

6. Запишите выражения для остаточных членов формулы Тейлора и изобразите их на графике:

Задание №7.2.

Запишите для заданной функции формулу Тейлора указанного порядка в окрестности точки х₀. Изобразите график функции и её многочлена Тейлора. Варианты заданий в Таблице №7.2.

Порядок выполнения задания:

Запишем формулу Тейлора четвёртого порядка для функции в окрестности точки х₀ = −1.

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) функцию f(x) и отдельно скопируйте её правую часть в рабочий документ:

3. Выполните замену переменной t = x – x₀ и запишите полученную функцию переменной t:

Для того, чтобы выполнить замену переменной х в функции f(x) скопируйте в буфер обмена стандартным для Windows способом выражение t + x₀ для х, выделите в выражении для f(x) переменную х и щёлкните по строке Подставить в пункте Переменная меню Символика:

4. Разложите функцию переменой t по формуле Тейлора в окрестности нуля:

5. Определите функцию переменной t, равную правой части формулы Тейлора, и выполните в ней замену х = t + x₀ (см. п.3):

6. Определите многочлен Тейлора заданной степени:

7. Постройте графики функции и её многочлена Тейлора:

Таблица №7.2

№	f(x)	x0	n	№	f(x)	x0	n
1		1	5	16		0	5
2		2	4	17		0	6
3		0	5	18		-1	5
4		1	6	19		-2	5
5		1	5	20		-1	5
6		0	6	21		1	5
7		0	6	22		2	4
8		2	5	23		0	5
9		2	6	24		1	6
10		-2	5	25		1	5
11		1	4	26		0	6
12		1	5	27		0	6
13		1	6	28		2	5
14		0	6	29		2	6
15		1	5	30		-2	5

Контрольные вопросы:

1. Запишите формулу Тейлора и определите в ней остаточный многочлен.

2. Перечислите известные вам формулы Тейлора для основных элементарных функций.

3. Что такое многочлен Тейлора? Каким образом его можно вычислить с помощью Mathcad?

Лабораторная работа №8

Неопределённый интеграл.

Цель работы

Вычисление неопределённого интеграла и построение графиков первообразных.

Порядок выполнения работы:

1. Вспомнить определения первообразной функции, семейства первообразных и неопределённого интеграла функции (см. Приложение Н).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №8.1.

Вычислите неопределённый интеграл и проверьте правильность вычислений; постройте графики семейства первообразных. Варианты заданий в Таблице №8.1.

Порядок выполнения задания:

Исходная функция: .

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) подынтегральную функцию как функцию переменной х:

3. Найдите первообразную функции х. Для этого щёлкните по кнопке панели , введите с клавиатуры в помеченных позициях подынтегральную функцию и переменную интегрирования, выделите всё выражение выделяющей рамкой, затем щёлкните по кнопке в панели . Первообразная, в которой по умолчанию значение произвольной константы равно нулю, будет отображена справа от стрелки:

4. Определите первообразную как функцию переменной. Для этого скопируйте вычисленное выражение и присвойте его функции переменной х:

5. Для того чтобы проверить первообразную, найдите её производную. Скопируйте в буфер обмена выражение первообразной, щёлкните по кнопке дифференцирования , вставьте из буфера обмена выражение первообразной (или F(x)), введите с клавиатуры переменную дифференцирования и дальше действуйте так же, как при символьном вычислении первообразной:

6. Упростите производную от первообразной, сравните результаты с подынтегральной функцией. Для этого скопируйте выражение для производной в рабочий документ, полностью выделите его рамкой и щёлкните по строке Упростить меню Символика:

7. Постройте на одном графике изображения нескольких первообразных:

Таблица №8.1

№	f(x)	№	f(x)	№	f(x)
1		11		21
2		12		22
3		13		23
4		14		24
5		15		25
6		16		26
7		17		27
8		18		28
9		19		29
10		20		30

Контрольные вопросы:

1. Дайте определение первообразной функции.

2. Что называется неопределённым интегралом функции? Запишите формулу вычисления неопределённого интеграла.

Лабораторная работа №9

Определённый интеграл.

Цель работы

Вычисление неопределённого интеграла и интегрирование заменой переменной.

Порядок выполнения работы:

1. Вспомнить определения определённого интеграла, формулу Ньютона – Лейбница и правила интегрирования заменой переменной (см. Приложение I).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №9.1.

«Определение и вычисление определённого интеграла»

Для заданной функции f(x) исследуйте поведение интегральных сумм на заданном отрезке интегрирования [a, b], разбивая отрезок интегрирования на N равных частей длины ∆ = . Вычислите определённый интеграл и сравните его значение со значениями пределов интегральных сумм. Варианты заданий в Таблице №9.1.

Порядок выполнения задания:

Исходная функция: ; заданный промежуток: [1, 5].

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите подынтегральную функцию как функцию переменной х и постройте её график:

3. Вычислите определённый интеграл. Для этого щёлкните в панели по кнопке и введите с клавиатуры в помеченных позициях пределы интегрирования, подынтегральную функцию и переменную интегрирования; выделите выражение, щёлкните по кнопке в панели . Вычисленное значение интеграла будет отображено в рабочем документе справа от стрелки:

4. Запишите выражение для интегральной суммы и вычислите её:

5. Разбейте отрезок [a, b] на N равных частей и определите три интегральные суммы как функции N, различающиеся способом выбора точки ξ_i на отрезке [x_i, x_i+1]: SI(N) для ξ_i = x_i, Sr(N) для ξ_i = x_i+1 и Sm(N) для ξ_i = . Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в левом конце отрезка разбиения. Найдите её предел при числе отрезков разбиения, стремящемся к бесконечности:

6. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в правом конце отрезка разбиения. Найдите её предел при числе отрезков разбиения, стремящемся к бесконечности:

7. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в середине отрезка разбиения. Найдите её предел при числе отрезков разбиения, стремящемся к бесконечности:

8. Сравните полученные значения предела между собой и со значением интеграла.

9. Постройте графики интегральных сумм как функций числа разбиения отрезка интегрирования:

10. Постройте графики интегральных сумм как функций длины отрезка разбиения:

Таблица №9.1

№	f(x)	[a, b]	№	f(x)	[a, b]
1		[0,3]	16		[-0.5,0.5]
2		[-1,1]	17		[5,10]
3		[-3,1]	18		[-1,3]
4		[-2,0]	19		[1,4]
5		[2,4]	20		[1,3]
6		[-1,3]	21		[-2,2]
7		[-0.4,0.6]	22		[-1,3]
8		[-3,1]	23		[-1.5,0.5]
9		[1,7]	24		[-2,2]
10		[-7,1]	25		[-2,2]
11		[1,5]	26		[-1,2]
12		[2,3]	27		[-1,1]
13		[-2,2]	28		[-1,1]
14		[2,4]	29		[-2,2]
15		[0,4]	30		[-1,1]

Задание №9.2.

«Формула Ньютона – Лейбница. Интегрирование заменой переменной»

Вычислите определённый интеграл средствами символьной математики и по формуле Ньютона – Лейбница от заданной функции по указанному отрезку. Варианты заданий в Таблице №9.2.

Порядок выполнения задания:

Исходная функция: ; заданный промежуток: [0, ].

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) подынтегральную функцию как функцию от х:

3. Найдите первообразную, используя символьную математику пакета (см. Задание №8.1, Лабораторная работа 8):

4. Определите первообразную как функцию переменной:

5. Вычислите определённый интеграл средствами символьной математики (см. Задание №9.1):

6. Вычислите определённый интеграл по формуле Ньютона – Лейбница:

7. Сравните полученные значения и сделайте соответствующий вывод.

Таблица №9.2

№	f(x)	[a, b]	№	f(x)	[a, b]
1		[0,16]	16		[6,10]
2		[0,1]	17		[0,3]
3		[0,5]	18		[1,64]
4		[3,5]	19		[0,3]
5		[0,]	20		[0,1]
6		[0,]	21		[3,5]
7		[0,4]	22		[0,]
8		[0,2]	23		[0,2]
9		[0,4]	24		[0,4]
10		[0,5]	25		[0,5]
11		[0,4]	26		[0,]
12		[0,2]	27		[0,]
13		[0,]	28		[0,3]
14		[6,9]	29		[6,9]
15		[8,12]	30		[8,12]

Контрольные вопросы:

1. Дайте определение определённому интегралу и интегральной суммы. Приведите пример.

2. Запишите формулу Ньютона-Лейбница. Приведите пример вычисления определённого интеграла с помощью формулы ьютона-Лейбница.

3. Запишите формулу замены переменной в определённом интеграле. Приведите пример.

Лабораторная работа №10

Несобственные интегралы.

Цель работы

Исследование функций, заданных интегралом; вычисление несобственных интегралов по неограниченному промежутку и от неограниченной функции по заданному отрезку непосредственно и через предел.

Порядок выполнения работы:

1. Вспомнить определения несобственного интеграла; условия, при которых несобственные интегралы сходятся и расходятся (см. Приложение J).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №10.1.

«Интеграл как функция верхнего предела»

Исследуйте функцию, заданную интегралом с заданным нижним пределом а и с переменным верхним пределом . Варианты заданий в Таблице №10.1.

Порядок выполнения задания:

Исходная функция: ; нижний предел а = 0.

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Введите выражение интеграла с переменным верхним пределом и вычислите его символьно:

3. Определите функцию, заданную введённым в предыдущем пункте интегралом; найдите значение функции при х = 0, 1 и 2:

4. Найдите первую и вторую производные определённой в предыдущем пункте функции:

5. Найдите горизонтальные асимптоты, если они существуют, вычислив пределы функции на ± ∞:

6. Постройте график функции, заданной интегралом:

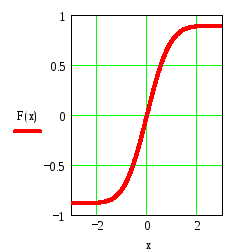
Таблица №10.1

№	f(t)	a	№	f(t)	a	№	f(t)	a
1		0	11		0	21		0
2		0	12		0	22		0
3		0	13		0	23		0
4		0	14		0	24		0
5		0	15		0	25		1
6		0	16		0	26		1
7		0	17		1	27		0
8		1	18		1	28		1
9		0	19		0	29		0
10		0	20		0	30		0

Задание №10.2.

«Несобственные интегралы по неограниченному пределу»

Вычислите несобственный интеграл по неограниченному промежутку непосредственно и через предел. Постройте график допредельной функции, заданной интегралом с переменным пределом. Варианты заданий в Таблице №10.2.

Порядок выполнения задания:

Исходный интеграл: .

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Введите выражение подынтегральной функции:

3. Вычислите несобственный интеграл от заданной функции по заданному неограниченному промежутку непосредственно – используя операцию вычисления определённого интеграла:

4. Определите функцию, заданную интегралом с переменным пределом:

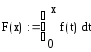
5. Вычислите соответствующий предел функции, определённой в предыдущем пункте:

6. Сравните полученные значения несобственного интеграла и сделайте соответствующие выводы.

7. Постройте график допредельной функции, определённой в п.3:

Таблица №10.2

№		№		№		№		№
1		7		13		19		25
2		8		14		20		26
3		9		15		21		27
4		10		16		22		28
5		11		17		23		29
6		12		18		24		30

Задание №10.3.

«Несобственные интегралы от неограниченных функций»

Вычислите несобственный интеграл от неограниченной функции по заданному отрезку непосредственно и через предел. Постройте график подынтегральной функции и график функции, заданной интегралом с переменным пределом. Варианты заданий в Таблице №10.3.

Порядок выполнения задания:

Исходный интеграл: .

1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Введите выражение подынтегральной функции:

3. Постройте график подынтегральной функции, чтобы убедиться в том, что она является бесконечно большой на одном их концов промежутка интегрирования:

4. Вычислите несобственный интеграл от заданной функции по заданному неограниченному промежутку непосредственно, используя операцию вычисления определённого интеграла:

5. Определите функцию, заданную интегралом с переменным пределом:

6. Вычислите предел функции, определённой в п.5:

7. Сравните полученные значения несобственного интеграла и сделайте соответствующие выводы.

8. Сформируйте таблицу значений переменного предела и таблицу соответствующих значений функции, заданной интегралом. Для этого необходимо сначала сформировать таблицу её значений F_i = F(ε_i) на сетке ε_i = 1 – , ε₀ = 1, ε₂₀ = 0:

9. Постройте график табличной функции, вычисленной в предыдущем пункте:

10. Сравните значение функции в нуле на графике с вычисленным значением несобственного интеграла и сделайте соответствующие выводы.

Таблица №10.3

№		№		№		№
1		9		17		25
2		10		18		26
3		11		19		27
4		12		20		28
5		13		21		29
6		14		22		30
7		15		23
8		16		24

Контрольные вопросы:

1. Дайте определение несобственному интегралу.

2. Опишите условия, при которых несобственный интеграл сходится и расходится.

Лабораторная работа №11

Числовые ряды.

Цель работы

Исследование на сходимость числовых рядов; вычисление сумм рядов.

Порядок выполнения работы:

1. Вспомнить основные определения числовых рядов, условия, при которых ряд сходится и расходится; теоремы сравнения и признаки сходимости рядов; признак сходимости Даламбера и Коши; определения знакопеременных и знакочередующихся рядов (см. Приложение К).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №11.1.

«Ряды с неотрицательными членами»

Исследуйте на сходимость числовые ряды , , и . Изобразите графики членов ряда и последовательности частичных сумм. Если удаётся, вычислите сумму ряда. Варианты заданий в Таблице №11.1.

Порядок выполнения задания:

Исходные числовые ряды: .

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Примените к ряду первую теорему сравнения и признаки сходимости, сравнивая его с обобщённым гармоническим рядом или с рядом типа прогрессии:

• - определите члены исследуемого ряда как функцию переменной n:

• - определите частичную сумму ряда как функцию переменной n:

• - постройте графики членов ряда и частичной суммы как функции переменной n:

• - вычислите сумму членов и частичной суммы ряда при n → ∞, сформулируйте и запишите соответствующий вывод:

Ряд сходится

По первой теореме сравнения ряд сходится:

3. Примените к ряду вторую теорему сравнения и признаки сходимости:

• - определите члены исследуемого ряда как функцию переменной n:

• - определите частичную сумму ряда как функцию переменной n:

степень больше 1, ряд сходится

• - вычислите предел членов ряда и частичной суммы при n → ∞, сформулируйте и запишите соответствующий вывод:

По второй теореме сравнения ряд сходится:

4. Примените к ряду признак Даламбера:

• - определите члены исследуемого ряда как функцию переменной n:

• - вычислите предел членов ряда согласно признаку сходимости Даламбера:

• - определите диапазон переменой n, постройте график членов ряда как функцию переменной n, сформулируйте и запишите соответствующий вывод:

По признаку Даламбера ряд расходится:

5. Примените к ряду признак Коши:

• - определите члены исследуемого ряда как функцию переменной n:

• - вычислите предел членов ряда согласно признаку сходимости Коши, сформулируйте и запишите соответствующий вывод:

По признаку Коши ряд сходится:

Таблица №11.1

№	an	bn	cn	dn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Задание №11.2.

«Знакопеременные ряды»

Исследуйте на сходимость числовые ряды , и . Изобразите графики членов ряда и последовательности частичных сумм. Если удаётся, вычислите сумму ряда. Варианты заданий в Таблице №11.1 (только три ряда).

Порядок выполнения задания:

Исследование числового ряда .

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите члены исследуемого ряда как функцию переменной n:

3. Определите абсолютную величину членов ряда как функцию переменной n:

4. Вычислите предел абсолютной величины членов ряда при n → ∞:

Ряд расходится

5. Определите диапазон переменной n и постройте график членов ряда и его абсолютной величины как функцию переменной n:

6. Исследуйте на сходимость ряд из абсолютных величин, сформулируйте и запишите соответствующий вывод об абсолютной или условной сходимости исследуемого ряда:

Ряд сходится условно

7. Повторите исследование по пунктам 2 – 6 для всех заданных числовых рядов.

Контрольные вопросы:

1. Дайте определение и запишите выражение числового ряда.

2. Что называют членом ряда и частичной суммой ряда?

3. Определите условия, при которых числовой ряд сходится и расходится.

4. Опишите теорему сравнения и признаки сходимости, с помощью которых исследуются на сходимость числовые ряды.

5. Какие ряды называются знакопеременными и знакочередующимися?

6. Определите условия, при которых числовой ряд является абсолютно сходящимся и сходящимся условно.

Лабораторная работа №12

Разложение элементарных функций в ряд Тейлора.

Цель работы

Исследование поведения частичных сумм ряда Тейлора заданной функции и разложение заданной функции в ряд Тейлора.

Порядок выполнения работы:

1. Вспомнить определения функционального и степенного ряда числовой последовательности и основные свойства разложения функции в ряд Тейлора (см. Приложение G и L).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №12.1.

Исследуйте поведение частичных сумм ряда Тейлора заданной функции. Исследуйте поведение остатка ряда. Варианты заданий в Таблице №12.1 (только f(x)).

Порядок выполнения задания:

Исходная функция: .

1. Установите автоматический режим вычислений.

2. Определите (запишите) функцию:

3. Используйте разложение функции по формуле Тейлора для записи ряда Тейлора функции:

4. Вычислите символьно сумму полученного ряда:

5. Запишите выражение частичной суммы ряда как функцию числа слагаемых и переменной х:

6. Постройте график функции и графики нескольких частичных сумм ряда:

7. Запишите выражение для соответствующих остатков ряда и постройте их графики:

Таблица №12.1

№	f(x)	x0	№	f(x)	x0	№	f(x)	x0
1		1	11		1	21		1
2		1	12		2	22		1
3		2	13		1	23		1
4		1	14		1	24		2
5		1	15		2	25		5
6		2	16		2	26		1
7		3	17		1	27		2
8		1	18		1	28		1
9		1	19		2	29		1
10		1	20		5	30		2

Задание №12.2.

Запишите для заданной функции разложение в ряд Тейлора в окрестности точки х₀. Изобразите график функции и графики нескольких частичных сумм ряда Тейлора. Варианты заданий в Таблице №12.1.

Порядок выполнения задания:

Исходная функция: ; заданная точка: х₀ = −2.

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите (запишите) функцию:

3. Выполните замену переменной t = x – x₀ и запишите полученную функцию переменной t:

Для того, чтобы выполнить замену переменной х в функции f(x) скопируйте в буфер обмена стандартным для Windows способом выражение t + x₀ для х, выделите в выражении для f(x) переменную х и щёлкните по строке Подставить в пункте Переменная меню Символика:

4. Используйте разложение функции переменной t по формуле Тейлора в окрестности нуля, чтобы записать для неё ряд Тейлора:

5. Определите частичную сумму ряда Тейлора как функцию числа слагаемых и переменной х:

6. Постройте графики функции f(x) и частичных сумм ряда Тейлора:

Контрольные вопросы:

1. Какой ряд называется рядом Тейлора? Приведите пример.

2. Запишите известные вам формулы разложения элементарных функций в ряд Тейлора.

Лабораторная работа №13

Разложение функций в ряд Фурье.

Цель работы

Исследование поведения частичных сумм ряда Фурье заданной функции, нахождение наилучшего приближения функции и сравнение сходимости ряда Фурье для двух заданных функций разной гладкости.

Порядок выполнения работы:

1. Вспомнить правила разложения функций в ряд Фурье, свойства коэффициентов Фурье, а также зависимость скорости сходимости ряда Фурье от гладкости функции (см. Приложение M).

2. Оформить отчёт: ответить на контрольные вопросы и выполнить в среде Mathcad задания по номеру своего варианта.

Задание №13.1.

«Сходимость ряда Фурье»

Исследуйте графически поведение частичных сумм ряда Фурье заданной функции f(x). Постройте графики частичных сумм для n = 1, 2, 5, 10, 20, 50. Вычислите значение частичных сумм ряда Фурье для n = 10, 20, 50 в точках x = −π, 0, , π. Варианты заданий в Таблице №13.1.

Порядок выполнения задания:

Исходная функция: f(x) = .

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите (запишите) заданную функцию переменной х. Для того, чтобы определить функцию, заданную разными аналитическими выражениями на разных промежутках необходимо использовать математическую панель инструментов Программирование . Порядок записи: введите имя функции переменной х; знак присваивания ; затем в панели Программирование – по кнопке . В рабочем документе справа от знака присваивания появится вертикальная черта с двумя помеченными строками для ввода. Перейдите в первую строку и щёлкните по кнопке , введите слева от if выражение для вычисления функции, а справа – соответствующее ограничение на аргумент. При вводе выражений используйте кнопки панелей калькулятора , знаков отношений и греческого алфавита . Аналогично введите выражение во второй строке. Постройте график функции:

3. Найдите выражения для коэффициентов Эйлера – Фурье и сохраните их в виде векторов a и b. Для этого определите размерность вектора n равной 50 и определите диапазон изменения номера k компонент векторов a и b от 0 до n. Определите выражение для частичной суммы ряда как функцию S(x, n) двух переменных x и π:

4. Постройте графики S(x, 1), S(x, 2), S(x, 5), S(x, 10), S(x, 20), S(x, 50) и сравните их между собой и с графиком f(x):

5. Вычислите значения частичных сумм S(x, 10), S(x, 20), S(x, 50) в точках х = −π, 0, , π:

6. Для х = х₀, где х₀ – точка непрерывности функции, постройте график частичной суммы S(x, n) как функции переменной n:

Таблица №13.1

Вариант 1 – 15	Выполните задание для функции f(x)=, где N – номер варианта.
Вариант 16 – 30	Выполните задание для функции f(x)= , где N – номер варианта.

Задание №13.2.

«Приближение функций. Минимальное свойство коэффициентов Фурье»

Найдите для заданного значения погрешности ε тригонометрический многочлен наилучшего приближения функции f(x) и наименьшей степени со среднеквадратичным отклонением, меньшим ε. Постройте график зависимости среднеквадратичного отклонения от степени многочлена. Варианты заданий в Таблице №13.2.

Порядок выполнения задания:

Исходная функция: ; среднеквадратическое отклонение ε = 0.02.

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите (запишите) заданную функцию переменной х:

3. Введите наибольшее значение n числа слагаемых в частичной сумме ряда Фурье, которое будет использовано в вычислениях. Если выбранного значения окажется недостаточно, его можно изменить:

4. Найдите выражения для коэффициентов Эйлера – Фурье:

5. Найдите выражения для частичной суммы ряда Фурье как функции переменных x и n:

6. Найдите выражение для среднеквадратического отклонения как функции степени тригонометрического многочлена n:

7. Выведите на экран таблицу значений σ(k) среднеквадратического отклонения для k от 1 до n. Для этого необходимо ввести в рабочий документ вектор s^T:

8. Сравнивая табличные значения σ(k) с заданным ε, найдите наименьшее k, для которого справедливо σ(k) < ε:

Наименьшее значение k = 12

9. Постройте график зависимости среднеквадратического отклонения от степени многочлена:

Таблица №13.2

Вариант 1 – 15	Выполните задание для функции f(x)=, где N – номер варианта. Значение ε положите равным 0.03.
Вариант 16 – 30	Выполните задание для функции f(x)= , где N – номер варианта. Значение ε положите равным 0.02.

Задание №13.3.

«Зависимость скорости сходимости ряда Фурье от гладкости функции»

Сравните сходимость ряда Фурье (поведение частичных сумм и выражения коэффициентов Фурье) для двух заданных функций разной гладкости. Варианты заданий в Таблице №13.3.

Порядок выполнения задания:

Исходные функции:

и .

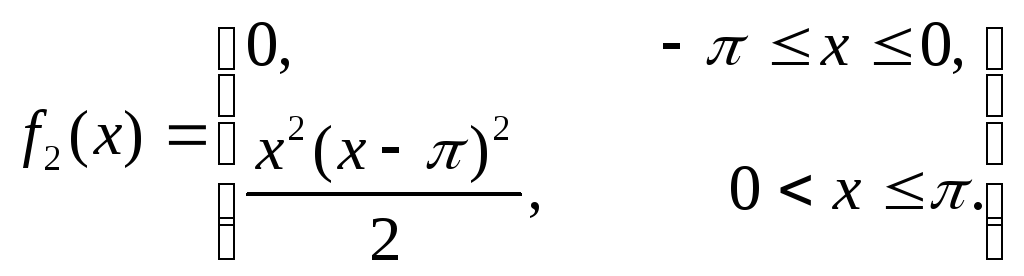1. Установите автоматический режим вычислений и режим отображения результатов вычислений по горизонтали.

2. Определите (запишите) функции и постройте их графики:

3. Найдите производные функции и постройте их графики:

4. Найдите выражения для коэффициентов Эйлера – Фурье для обеих функций:

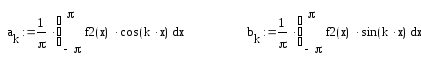
5. Найдите выражения для частичных сумм ряда Фурье как функции переменных х и n для обеих функций:

6. Найдите выражения для среднеквадратичных отклонений для обеих функций:

7. Постройте графики частичных сумм и среднеквадратичных отклонений для обеих функций:

8. Выведите выражения для коэффициентов Фурье обеих функций и вычислите их аналитически. При необходимости результаты вычислений необходимо упростить. Сравните степени номеров коэффициентов в знаменателях полученных выражений. По причине громоздкости расчётов, их результаты в пример не вошли.

Таблица №13.3

Вариант 1 – 15	Выполните задание для функции f1(x)=, f2(x)= где N – номер варианта.
Вариант 16 – 30	Выполните задание для функции f1(x)= , f2(x)= где N – номер варианта.

Контрольные вопросы:

1. Приведите пример тригонометрического ряда Фурье.

2. Запишите формулу Эйлера-Фурье для вычисления коэффициентов тригонометрического ряда Фурье.

3. Что называется тригонометрическим многочленом наилучшего приближения n-ой степени функции f(x)?

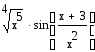
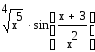
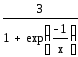
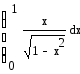
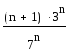
93