
Лабораторная работа №1
Построение и решение моделей линейного программирования организационных и
производственных систем
1.1. Цель работы
Построение, решение и анализ моделей линейного программирования.
1.2. Задание на лабораторную работу
Построить модель, используя аппарат линейного программирования и найти оптимальный вариант функционирования смоделированного информационного объекта.
1.3. Порядок выполнения работы
Оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного информационного объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Рассмотрим примеры задач линейного программирования.
Пример 1. Предприятие выпускает продукцию четырех видов: П1, П2,
П3, П4, для изготовления которой требуются ресурсы: трудовые, сырье,
финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа (норма расхода), прибыль, получаемая от реализации единицы каждого типа продукции, запасы ресурсов, приведены в табл.2.1. Требуется определить план выпуска продукции, при котором прибыль от реализации будет максимальной.
|
|
|
|
|
|
Таблица 2.1 |
|
Вид |
П1 |
П2 |
П3 |
П4 |
Запасы |
|
ресурса |
|
|
|
|
ресурса |
Трудовые |
1 |
1 |
1 |
1 |
16 |
|
Сырье |
6 |
5 |
4 |
3 |
110 |
|
Финансы |
4 |
6 |
10 |
13 |
100 |
|
Прибыль |
60 |
70 |
120 |
130 |
|
|
от |
реализации |
|
|
|
|
|
прдукции, тыс.руб.
Математическая модель задачи выглядит следующим образом:
пусть xi – количество продукции каждого вида, оптимальный выпуск которой необходимо определить.
f (x) = 60x1 + 70x2 + 120x3 + 130x4 max
x1 + x2 + x3 + x4 16
6x1 + 5x2 + 4x3 + 3x4 110 4x1 + 6x2 + 10x3 + 13x4 100 xj 0, j = 1,2,3,4
Для решения задачи необходимо:
создать форму для ввода условий задачи;
ввести исходные данные;
ввести зависимости из математической модели;
указать назначение целевой функции (min, max);
ввести ограничения и граничные условия.
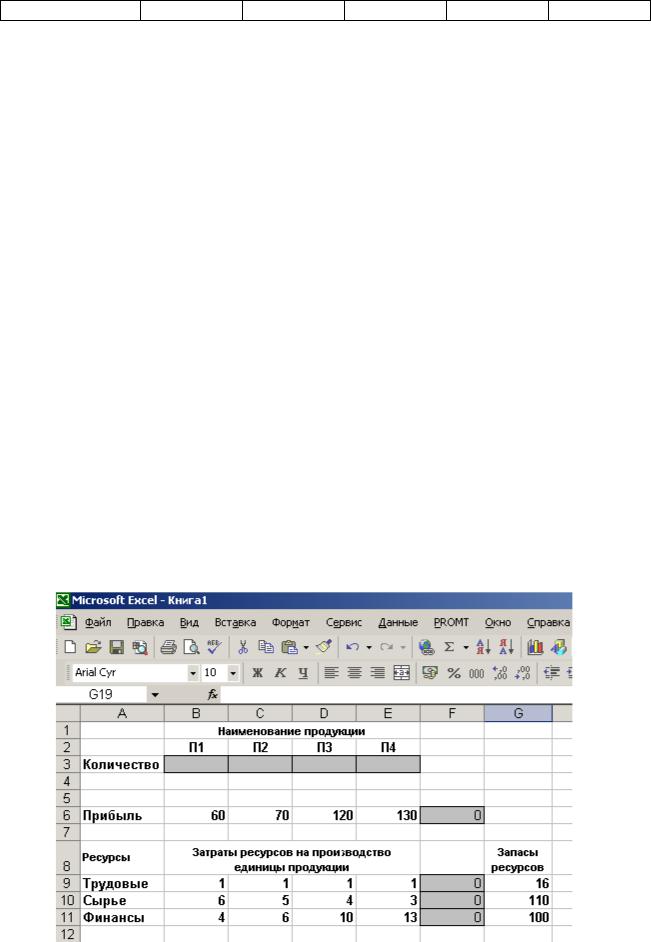
Форма для ввода условий задачи с исходными данными выглядит
следующим образом (табл.2.2):
Табл.2.2.
Ячейки В3:Е3 зарезервированы под результат (xi – количество продукции каждого вида, оптимальный выпуск которой необходимо определить).
Ячейки F6, F9:F11 содержат зависимости из математической модели,
которые вводятся следующим образом.
Ввести зависимость для целевой функции:
Курсор в F6.
Курсор на кнопку Мастер функций.
Курсор в окно Категория на категорию Математические.
Курсор в окно Функции на СУММПРОИЗВ.
В массив 1 ввести В$3:E$3.
В массив 2 ввести В$6:E$6.
Ввести зависимости системы ограничений:
Курсор в F9.
Курсор на кнопку Мастер функций.
Курсор в окно Категория на категорию Математические.
Курсор в окно Функции на СУММПРОИЗВ.
В массив 1 ввести В$3:E$3.
В массив 2 ввести В$9:E$9.
аналогично ввести условия ограничения в ячейки F10, F11.
Работа в диалоговом окне Поиск решения.
Курсор Сервис, Поиск решения
В диалоговом окне Поиск решения назначить целевую функцию:
Курсор в окно Установить целевую ячейку.
Ввести адрес: F6.
Ввести направление целевой функции: Максимальному значению.
Ввести адреса искомых переменных:
Курсор в поле Изменяя ячейки.
Ввести адреса: В3:Е3.
Курсор Добавить
Вдиалоговом окне Добавление ограничения ввести граничные условия на переменные (xj 0, j = 1,2,3,4)
В окне Ссылка на ячейку ввести В$3:E$3
Курсор на стрелку (на экране: знаки для ввода ограничения).
Курсор на знак >=.
Курсор в правое окно.
Ввести «0»
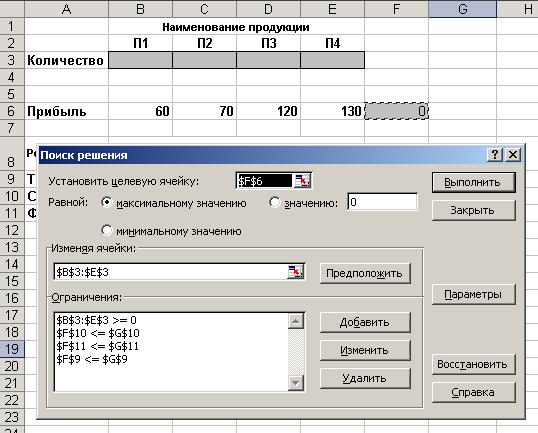
Ввести граничные условия системы ограничений: $F$9 <= $G$9, $F$10 <= $G$10, $F$11 <= $G$11.
После ввода последнего ограничения вместо Добавить... ввести ОК.
На экране: диалоговое окно Поиск решения с введенными условиями.
Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью команд Изменить...Удалить.
На этом ввод условий задачи заканчивается. Следующий шаг - решение задачи.
Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения.
Параметры...
На экране диалоговое окно Параметры поиска решения.
С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. С наиболее важными командами, применимыми при решении конкретных задач, мы будем знакомиться по мере необходимости. Вместе с тем, команды, используемые по умолчанию, подходят для решения большей части практических задач.
Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.
ОК
На экране: диалоговое окно Поиск решения.
Выполнить
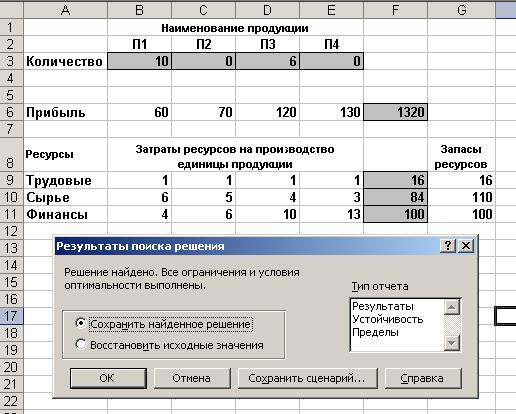
На экране: диалоговое окно Результаты поиска решения. Решение найдено и результат оптимального решения задачи приведены в табл.2.4.
Табл. 2.4.
Примечание.
Решение задачи находится не всегда. Если условия задачи несовместны,
на экране в диалоговом окне Результаты поиска решения появляется
сообщение: Поиск не может найти подходящего решения.
Если целевая функция не ограничена, то появляется сообщение:
Значения целевой ячейки не сходятся.
Необходимые действия в этом случае требуют определенной квалификации исследователя и при необходимости будут рассмотрены на лабораторных занятиях.
Пример 2. Фирма объединяет 5 предприятий, каждое из которых производит 3 вида изделий. Производительность каждого предприятия при изготовлении одного изделия (в денежных единицах) характеризуется следующей таблицей:
ПРЕДПРИЯТИЯ |
|
ИЗДЕЛИЯ |
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
1 |
15 |
6 |
12 |
|
|
|
|
2 |
6 |
9 |
13 |
|
|
|
|
3 |
8 |
11 |
2 |
|
|
|
|
4 |
7 |
13 |
6 |
|
|
|
|
5 |
4 |
9 |
12 |
|
|
|
|
Учитывая необходимость специализации каждого предприятия только по одному изделию, распределить производство изделий по предприятиям так,
чтобы суммарная производительность фирмы при этом распределении была максимальной. Проверить правильность полученного результата, решив задачу,
используя венгерский метод.
Составим математическую модель задачи.
Чтобы сформулировать задачу о назначениях математически, введем переменную величину xij, отражающую факт специализации предприятия на производстве изделий:
xij = |
1 |
, |
|
|
0 |
, |
|
|
|
||
1 - если на i-м предприятии выпускают j-ое изделие;
0 - в противном случае.
Задача примет вид:
n |
|
n |
|
Целевая функция = |
C ij x ij |
max |
|
i |
1 |
j 1 |
|
1 5 x1 1 6 x1 2 1 2 x1 3 6 x2 1 9 x2 2 1 3 x2 3 8 x3 1 1 1 x3 2 2 x3 3 7 x4 1
1 3 x4 2 6 x4 3 4 x5 1 9 x5 2 1 2 x5 3 |
m a x |
|||
x1 1 x1 2 x1 3 |
1 |
|
||
x2 1 |
x2 2 |
x2 3 |
1 |
|
x3 1 |
x3 2 |
x3 3 |
1 |
|
x4 1 |
x4 2 |
x4 3 |
1 |
|
x5 1 |
x5 2 |
x5 3 |
1 |
|
x1 1 |
x2 1 |
x3 1 x4 1 x5 1 |
1 |
|
x2 1 |
x2 2 |
x2 3 |
x2 4 x2 5 |
1 |
x3 1 |
x3 2 |
x3 3 |
x3 4 x3 5 |
1 |
Чтобы решить задачу (получить оптимальный план назначения), сначала нужно ввести значения исходной матрицы производительности и зарезервировать ячейки для результата (оптимального плана назначения).

Так как в заданной матрице производительности m n, то добавляем к ней два столбца нулей (выделены желтым). Затем резервируем ячейки для целевой функции и добавочных ограничений (выделены рыжим, бирюзовым и голубым цветами), причем ЦФ записывается как СУММПРОИЗВ, а ограничения – как СУММ (сумма значений либо по строке – голубой, либо по столбцу – бирюзовый цвет).
Вводим формулу СУММПРОИЗВ(C6:G10;B14:F18) (в ячейку целевой функции E$22) и ограничения в ячейки B$19:F$19 и G$14:G$18.
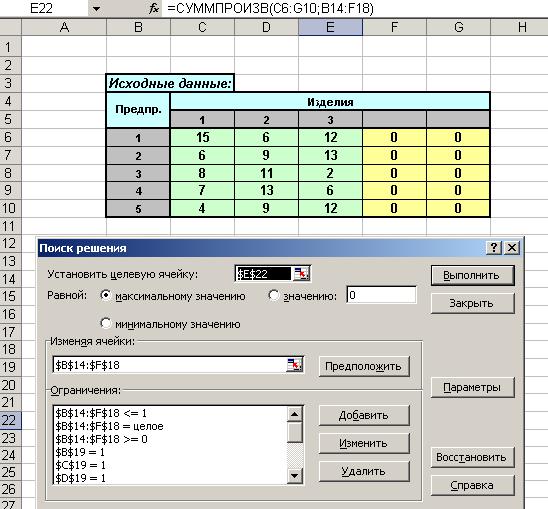
Ограничения такие: суммы по строкам и суммы по столбцам оптимального плана назначения должны быть равны 1.
После ввода всех ограничений нажимаем Выполнить, получаем результаты поиска решения:
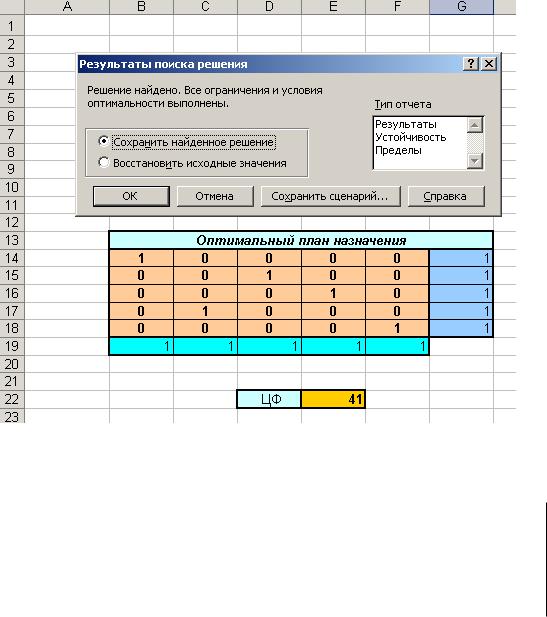
Сохраняем результат. Получаем решенную задачу.
Проверка результата расчета венгерским методом.
|
1 5 6 |
1 2 |
0 |
0 |
|
0* |
7 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
|
6 |
9 |
1 3 0 |
0 |
|
9 |
4 |
0* |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
|
8 |
1 1 2 |
0 |
0 |
|
7 |
2 |
1 1 0* |
0 |
|
0 0 |
0 1 0 |
|||||
|
7 |
1 3 6 |
0 |
0 |
|
8 |
0* |
7 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
|
4 |
9 |
1 2 |
0 |
0 |
|
1 1 4 |
1 |
0 |
0* |
|
0 |
0 |
0 |
0 |
1 |
|
max 15 13 13 0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
К заданной матрице производительности приписываем два столбца нулей, выбираем максимальный элемент по каждому столбцу (15, 13, 13, 0, 0) и вычитаем из него все другие элементы столбца. Получаем матрицу, в
которой выделяем систему независимых нулей ( 0 * ). Так как число независимых нулей равно порядку матрицы, то после первой же итерации задача решена. Независимые нули заменяются единицами, а все остальные элементы – нулями. Получили оптимальный план назначения.
Вывод.
При решении задачи в EXCEL и при проверке результата расчета с использованием венгерского метода решения задачи о назначениях
