9. Огибающая семейства плоских кривых

Кривая называется огибающей семейства кривых , если:

1. она касается каждой кривой семейства;

2. каждая ее точка является точкой ее касания с кривой семейства, отличной от нее самой.

Огибающая семейства кривых , если она существует, находится исключением параметраиз уравнений

и

Может, однако, случится, что полученная этим способом кривая будет не огибающей, а геометрическим местом особых точек кривых семейства.

10. Касательная плоскость и нормаль к поверхности

Пусть поверхность задана уравнением ; возьмем на ней точку

Уравнения нормали к поверхности этой точки будут:

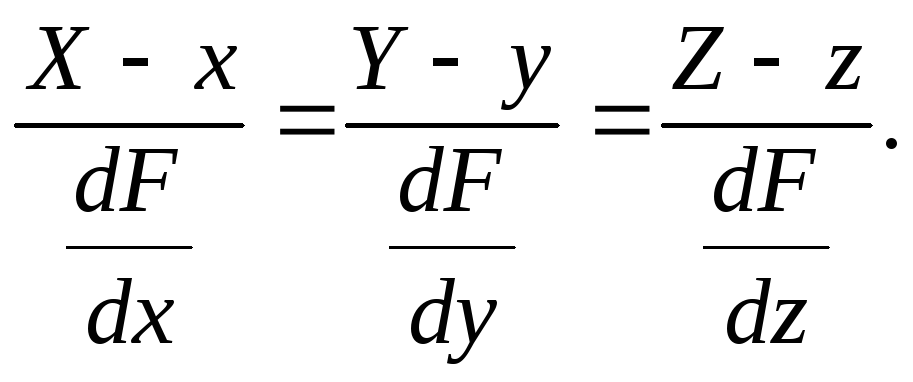(10.1)

Уравнение касательной плоскости:

(10.2)

В уравнениях (10.1) и (10.2) - текущие координаты нормали или касательной плоскости.

Вектор назовем нормальным вектором поверхности.

Если на поверхности есть точка, в которой то она называется особой. В такой точке нет ни касательной, ни плоскости, ни нормали к поверхности.

11. Скалярное поле. Линии и поверхности уровней. Производная в данном направлении. Градиент

Уравнение определяетв каждой точкенекоторой области, которая называетсяполем скаляра . Вдоль каждой из линийгде- постоянные, скаляростается постоянным и меняется только при переходе точкис одной линии на другую. Эти линии называютсяизолиниями (изотермами, изобарами и т.п.) илилиниями уровней.

Уравнение определяетполе скаляраи в некоторой части трехмерного пространства.Изоповерхностями, илиповерхностями уровней будут:

…

Пусть точка перемещается по прямойсо скоростьюТогда скалярбудут изменятся со скоростьюгде-нормальный векторповерхности, а- единичный вектор направления 1.

Производная

называется производной от функциив данном направлении .

Градиентомскаляраназывается вектор

Градиент есть вектор скорости наибыстрейшего изменения скаляра.

12. Экстремум функции двух переменных

Необходимые условия. Функция может иметьэкстремумтолько в точках, в которыхиэти точки называютсякритическими.

Достаточные условия. Обозначим через изначения производных

в критической точке

Тогда если:

1. топри,при

2. то экстремума нет;

3. то экстремум может быть, а может и не быть (сомнительный случай).

Условный экстремум. Чтобы найти экстремум функции при условии, чтоисвязаны уравнениемсоставим вспомогательную функцию

Координаты экстремальной точки должны удовлетворять трем уравнениям:

Из которых и находятся и

Задачи

1. Построить геометрическое изображение однозначной функции , определяемой уравнением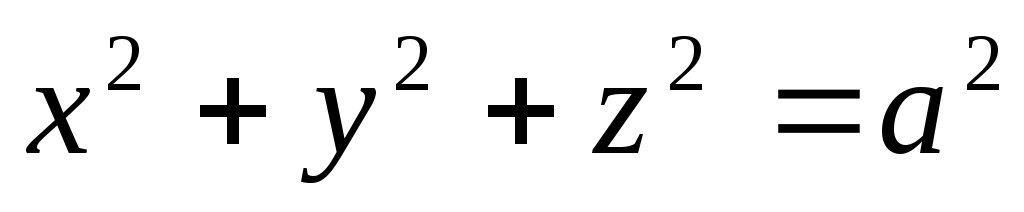, положенной в областии отрицательной вне ее. Указать линию ее разрыва.

2. Показать, что уравнение определяет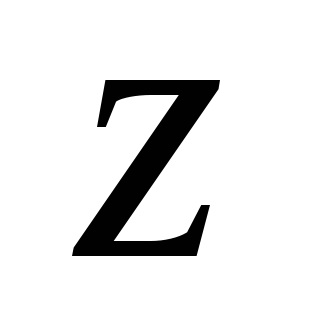как бесчисленное множество однозначных функци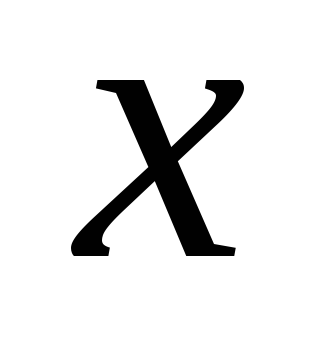йи, из которых две непрерывны. Указать область определения всех этих функций, положительной в областии отрицательной вне ее.

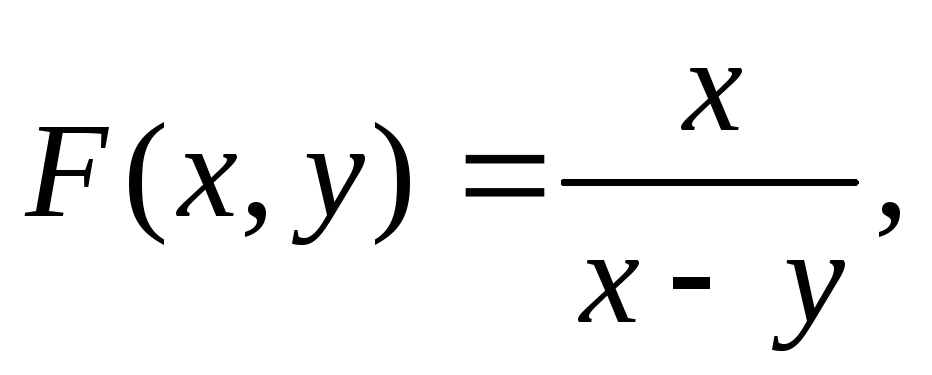3. Доказать, что если то

4. указать области определения функций:

1) 2)3)4)5)6)

5. Показать, что уравнение определяеткак бесчисленное множество функцийи, из которых две непрерывны. Указать область определения всех этих функций и построить геометрическое изображение положительной непрерывной функции. Привести пример однозначной, но разрывной функции, определяемой тем же уравнением

6. Доказать, что если , то

7. Доказать, что если , то

8. Доказать, что если то

9. Доказать, что если то

10. Катеты прямоугольного треугольника, измеренные с точностью до 0,1 см, оказались равными 7,5 см и 18 см. Определить абсолютную погрешность при вычислении гипотенузы.

11. При деформации цилиндра его радиус увеличился с 20 см до 20,5 см, а высотауменьшилась со 100 см до 98 см. найти приближенно изменение объемапо формуле

12. Найти значение идля функции, когдаизменяется от 2 до 2,1; а- от 1 до 0,9.

13. Подсчитать приблизительно изменения функции когдаизменяется от 5 до 4,5; а- от 3 до 3,3.

14. Найти из уравнений:

1)

2)

15. Доказать, что если , где, то

16. Доказать, что если где, то

17. Пусть . Выразитьичерези, если 1)

2)

18.

Найти угловой коэффициент касательной к кривой.

19. Доказать, что если , то

20. Показать, что дифференциальному уравнению удовлетворяет неявная функция, определяемая уравнением (конических поверхностей)

21. Найти из уравнений:

22. Показать, что функция при любых дважды дифференцируемых функцияхиудовлетворяет дифференциальному уравнению

23. Пусть Найтии.

24. Найти частные производные второго порядка функции

25. Доказать, что если , то

26. Определить области расположения, точки пересечения с осями координат, особые точки кривых и построить кривые:

1) 3)

2) 4)

27. Найти точки пересечения с осями координат, особую точку и симптому кривойи построить кривую.

28. Определить области расположения, особые точки и асимптоты кривых:

1) 4)

2) 5)

3) 6).

29. Найти огибающую семейства парабол, имеющих ось симметрии, параллельную оси , и проходящих через точкипри различных.

30. Отрезок постоянной длинны скользит своими концами по координатным осям. Найти огибающую семейства таких отрезков.

31. Найти огибающую семейства окружностей, проходящих через начало координат и имеющих центр на параболе

32. Из начала координат выпускается снаряд с начальной скоростью под угломк оси. Найти огибающую семейства траекторий при различных.

33. Найти огибающую 1) семейства прямых при постоянном; 2) семейства прямых3) семейства кубических парабол

34. Написать уравнения касательной плоскости к поверхности: