4.6 Мажоритарные элементы.

Еще одним узлом, которое относится к схемам контроля и используется для построения высоконадежных цифровых схем, является мажоритарный элемент.

В любом устройстве возможны нарушения нормальной работы – сбои (ошибки), которые могут возникать как из-за возникновения неисправностей, так и по причинам воздействия помех. Один из методов повышения надежности функционирования цифровых систем заключается в обнаружении и последующем устранении возникающих ошибок.

Однако в ряде случаев их появление недопустимо, то есть вероятность возникновения ошибки должна быть сведена к нулю. В таких ситуациях используется резервирование узлов, блоков и отдельных элементов аппаратуры. То есть несколько устройств включаются в работу параллельно и решают одну и ту же задачу. Если они функционируют правильно, то формируют идентичные результаты. В большинстве ситуаций, в случае нарушения работоспособности или выхода из строя ряда из них, остальные продолжат нормальное функционирование. В этом случае для обеспечения надежной работы системы потребуется некоторый узел, который пропускал бы на ее выход сигналы только с правильно работающих блоков.

Один из способов решения этой задачи заключается в использования мажоритарных элементов, работу которых можно описать следующим образом. Пусть в системе используется трехкратное дублирование, то есть имеется три одинаковых узла , формирующих при нормальном функционировании идентичные одноразрядные двоичные сигналы.

П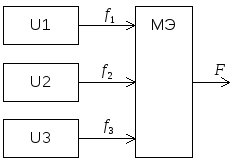ри нарушении работы одного из них, его сигнал окажется противоположен формируемым двумя остальными. В этом случае правильное значение выходного сигнала должно совпадать с состоянием большинства из устройств.

Таблица, описывающая работу трехвходового мажоритарного элемента, имеет вид. На его выходе формируется сигнал, идентичный большинству из поступивших на входы. Функция, описывающая работу такого устройства, описывается выражением

.

Воспользовавшись правилами алгебры логики, либо построив карту Карно, данное выражение можно упростить до. Внутренняя структура такого элемента имеет вид, а на принципиальных схемах он изображается следующим образом.

Очевидно, что мажоритарный элемент может иметь только нечетное количество входов, 3,5,7 и т.п., так как в противном случае при равенстве числа правильных и неверных сигналов, принять решение о выборе невозможно. Кроме того, от самого мажоритарного элемента требуется очень высокая надежность, так как в случае выхода его из строя, вся схема резервирования окажется бесполезной.

Достаточно просто можно создать устройство, которое в схеме с мажоритарным элементом будет формировать двоичный код номера узла, вырабатывающего ложный сигнал. Таблица его функционирования имеет вид. Нулевому коду соответствует правильное функционирование всех узлов, то есть совпадение всех сигналов, в противном случае формируется код номера устройства, состояние выхода которого не совпадает с остальными.

Аналитические выражения для функций, описывающих соответствующие разряды, можно получить, используя карту Карно, однако проанализировав структуру таблицы, можно увидеть, что значенияне зависят оти описываются функцией логической неравнозначности для сигналов, то есть. Разрядв первых четырех строках таблицы совпадает с, а на остальных принимает инверсные по отношению к этой функции значения. При этом прямые реализуются при, а инверсные в случае, независимо от состояния. Таким образом, для реализацииможно использовать управляемое инвертированиепо единичному значению. Данная процедура соответствует выполнению функции логической неравнозначностии реализуется логическим элементом – сумматором по модулю два.