4.10 Сумматоры двоично-десятичных кодов.

Цифровые данные, предназначенные, в частности, для систем отображения информации часто представляются и обрабатываются в кодах, отличных от двоичного, например в двоично-десятичном. Его особенность в том, что каждая цифра десятичного числа преобразуется в четырехразрядную двоичную комбинацию (тетраду) независимо от других.

Т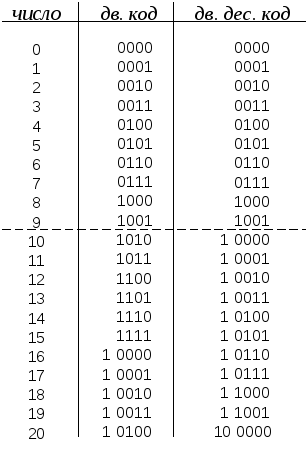ак как цифр десять, то некоторые комбинации, имеющиеся в четырехразрядном двоичном коде, в двоично-десятичном будут отсутствовать. Как следует из таблицы, для чисел в пределах от 0 до 9 они совпадают, а далее начинаются отличия, связанные как со структурой тетрад, так и с формированием переносов в старшие разряды кодов.

В стандартных позиционных кодах каждый разряд имеет свой вес, равный соответствующей степени основания системы счисления. В двоично-десятичном коде, используется двойное взвешивание. Одноименные разряды всех тетрад имеют одинаковые веса 8,4,2 и 1, а самим тетрадам приписываются веса кратные степеням 10.

Суммировать числа, представленные в двоично-десятичном коде и получать аналогичный результат, можно используя стандартные подходы, либо уже имеющиеся технические решения. В частности, если преобразовать двоично-десятичные коды операндов в двоичные, то для их сложения можно использовать двоичные сумматоры, а р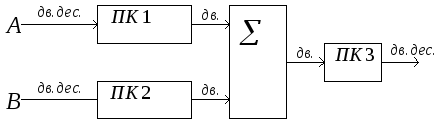езультат трансформировать в двоично-десятичный код с помощью дополнительного преобразователя. Однако такое решение получается громоздким.

Если создать сумматор двоично-десятичных кодов для одной тетрады, то объединяя такие узлы по входам и выходам переноса, можно наращивать разрядность обрабатываемых операндов. Так как комбинации двоично-десятичного кода тетрады совпадают с соответствующими для двоичного, то их можно складывать в четырехразрядном двоичном сумматоре.

Результат будет верным, пока значение суммы не превысит 9, то есть вплоть до кодовой комбинации 1001. Далее на выходах сумматора начнут формироваться кодовые комбинации, которых не существует в двоично-десятичном коде. Кроме того, пока результат лежит в пределах от 10 до 15 переноса в двоичном сумматоре нет, а в двоично-десятичном он должен появиться.

Таким образом, здесь потребуется коррекция результата. При сложении, к примеру, чисел 7 и 5 (их коды 0111 и 0101) в двоичном сумматоре получится код числа 12 (1100). В двоично-десятичном коде результат должен выглядеть как 1 0010, то есть как 10 и 2 по отдельности. Такое преобразование можно осуществить, если из исходного числа вычесть 10 и сформировать сигнал переноса в следующую тетраду.

Для реализации корректора потребуется устройство анализа выходного кода двоичного сумматора, которое формировало бы, к примеру, сигнал равный нулю, если код меньше или равен 9, и единичный в остальных случаях. Здесь можно использовать параллельный четырехразрядный цифровой компаратор, но целесообразнее построить специальное устройство. Оно окажется проще, так как в данной ситуации требуется сравнивать код с конкретным числом.

Таблица, определяющая связь между выходными сигналами сумматора и функцией анализатора имеет вид.

Из нее следует, что , еслии, либоиравны единице. В остальных случаях искомая функция обращается в нуль. Таким образом она имеет вид.

Чтобы провести коррекцию необходимо в случае, когда вычесть из кода, сформированного сумматором число 10. С этой целью потребуется прибавить к его результату дополнительный код десяти, то есть число 6 (кодовая комбинация 0110). Таким образом, в схеме потребуется дополнительный двоичный сумматор, в котором, еслиисходный результат складывался бы с нулем, а при- с шестеркой.

Сравнивая коды этих чисел (0110 и 0000), можно сделать вывод, что на входы ивторого сумматора должны быть поданы логические нули, а на входыисигнал, соответствующий значению функции.

Результат сложения двоично-десятичных кодов может оказаться больше 15. Например, при сложении чисел 9 и 8, сумма получается равной 17. В двоичном сумматоре при этом появится сигнал переноса и на его выходах сформируется кодовая комбинация 1 0001. , и результат не будет скорректирован, хотя это требуется.

П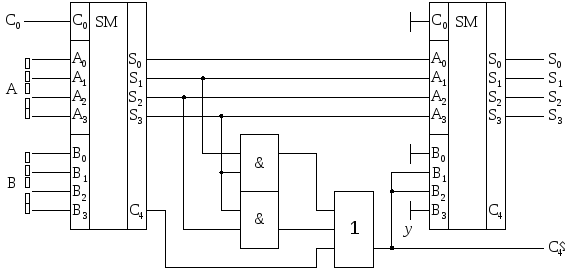роцедурав данной ситуации проводится следующим образом. Двоичный сумматор представляет число 17 как 16+1, но 16=10+6, а 17=10+6+1. Наличие 10 говорит о том, что должен сформироваться сигнал переноса в следующую тетраду, а кроме того, к результату работы первого сумматора требуется прибавить 6. Это можно сделать. принудительно установив при возникновении переносаединичное значение функции, для чего ее необходимо представить в виде. При этом схема сумматора двоично-десятичных кодов чисел будет выглядеть следующим образом.