Планирование эксперимента

________________________________________________________________________________

В реальных условиях, из-за наличия помехи  , экспериментатор измеряет величину y вместо истинного значения выходной величины  . Следовательно, опираясь на результаты измерения, нельзя получить абсолютно точных значений . Вместо истинных параметров  приходится использовать случайные величины. Обозначим эти величины b и назовем их оценками . Тогда, оцениваемое уравнение для модели будет иметь вид:

Y=Y(x,b) (4.12)

4.4. Общие требования, предъявляемые к оценкам

Чтобы правильно и точно оценить параметры модели, оценки должны быть: несмещенными, состоятельными, эффективными и достаточными.

Оценки b являются несмещенными , если их математические ожидания равны истинным значениям параметров:

M[b]=.

Это значит, что в процессе вычисления параметров модели не должны возникать статистические ошибки.

Оценка называется состоятельной, если при увеличении числа наблюдений n до бесконечности она сходится по вероятности к истинному параметру:

Достаточное условие для этого

Оценки будут эффективными, если они позволяют получить максимальную информацию из наблюдений. Часто бывает , что из исследуемого параметра можно найти несколько состоятельных оценок. Чтобы выбрать одну из них сравнивают дисперсии всех оценок и по минимуму дисперсии получают оценку, которая и будет эффективной

,

где D[b] - дисперсия оценки b, - дисперсия любых других несмещенных оценокb.

Пример. Дано n наблюдений случайной величины X. Возникает вопрос, какую величину принять за оценку математического ожидания: среднее выборки или медиану. Известно, что величина X распределена по нормальному закону с дисперсиями: и,

где - среднее выборки;- медиана;n - объём выборки; - дисперсия генеральной совокупностиX. Так как , то оценка средней выборки будет эффективной.

Критерии несмещенности и эффективности следует рассматривать одновременно. Может оказаться, что смещенная оценка с меньшей дисперсией будет более предпочтительной, чем несмещенная оценка с большей дисперсией.

4.5. Методы оценивания параметров

Существует несколько различных методов оценивания параметров:

• максимального правдоподобия;

• моментов;

• оценивание по Байесу;

• наименьших квадратов.

Метод максимального правдоподобия базируется на использовании априорной информации, полученной из эксперимента. Получают выборку значений случайной величины X(x₁,x₂,...,x_n). Рассматривают оцениваемые параметры  как случайные величины с некоторым законом распределения вероятности. Затем это распределение перестраивается таким образом, чтобы получить апостериорное распределение вероятности, плотность которого несет информацию о возможных значениях  на основе экспериментальных данных X. Этот метод приводит к эффективным и состоятельным оценкам, однако оценки могут быть смещенными.

Метод моментов является одним из наиболее старых методов. При его использовании вычисляются первые n моментов случайной величины, которые затем приравниваются выборочным моментам. После этого находят n значений оцениваемых параметров .

Оценивание по Байесу как и метод максимального правдоподобия основывается на использовании априорной информации. Определяется плотность распределения вероятностей x, и на основе апостериорной информации принимается решение.

Метод наименьших квадратов (МНК) является самым распространенным методом при оценивании параметров модели. Поэтому рассмотрим его более подробно на примере линейной модели с одной независимой величиной.

Уравнение модели с одной независимой величиной имеет вид:

(4.13)

Оценкой уравнения (4.13) будет:

(4.14)

Уравнение (4.13) на плоскости представляет теоретическую линию регрессии, а (4.14) эмпирическую линию регрессии (рис.4.2). Коэффициенты b₀ и b₁ являются оценками истинных коэффициентов ₀ и ₁.

На рис.4.7 обозначены точки (y_ij,x_i) - одно измерение; - выборочное среднее наблюдение приx_i; - предсказанное значение выходной величины y_i при x_i; - истинное значение выходной величины_i при x_i. Для несмещенных оценок , т.е._i есть математическое ожидание при.

По результатам опыта вычисляются коэффициенты b₀ и b₁ . Если бы все экспериментальные точки оказались на теоретической линии регрессии, то или

, i=1,2,...n (4.15)

и тогда коэффициенты ₀ и ₁ могли быть определены решением системы уравнений (4.15).

Однако, в реальных условиях левая часть (4.15) отличается от нуля на величину _i

(4.16)

Рис.4.7.

а – теоретическая линия регрессии; б –эмпирическая линия регрессии.

Величина _i называется невязкой. Она может быть вызвана ошибкой эксперимента или неправильным выбором линейной модели. Поэтому возникает задача найти такие коэффициенты уравнения регрессии, при которых невязка будет минимальной. Лучшей оценкой является выражение . Это выражение приводит к методу наименьших квадратов:

(4.17)

где - число повторных измерений величиныy при данном значении x_i.

Минимум функции Ф достигается при одновременном равенстве нулю частных производных этой функции по всем искомым коэффициентам:

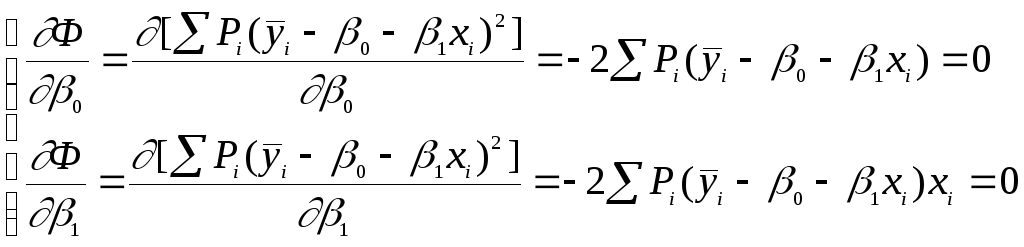(4.18)

После замены ₀ и ₁ их оценками b₀ и b₁ получаем систему нормальных уравнений:

или

(4.19)

Решая систему нормальных уравнений относительно b₀ и b₁ получаем:

(4.20)

(4.21)