- 9-

Работа 3.10 Туннельный эффект в вырожденном p-n-переходе.

Цель работы: Изучение элементов теории туннельного эффекта; исследование проявлений туннельного эффекта в туннельном диоде.

Теоретическое введение

1. Пусть в некоторой области пространства имеется потенциальный барьер

конечной высоты и ширины(рис 1,а). Тогда, по классическим представлениям, частица с энергией всегда преодолевает барьер, а частица с энергией, меньшей , от него зеркально отражается.

В действительности существуют отличные от нуля вероятности отражения частицы с энергией и проникновения (туннелирования) частиц с энергией.

2. Туннельный эффект может быть количественно исследован путем решения основного уравнения квантовой механики – уравнения Шредингера – с использованием свойств непрерывности волновой функции и ее производных в местах скачка потенциальной функции.

Общее решение стационарного уравнения Шредингера в одномерной, как на рис.1, а, задаче

(1)

где – потенциальная функция, имеет вид

,

а волновое число определяется из выражения

.

Вразличных областях пространства (области 1,2 и 3 на рис.1,а) уравнению (1) удовлетворяют различные волновые функции. Учитывая, что волновая функция испытывает «отражение» только в местах разрыва потенциальной функции, получаем следующие решения:

(2)

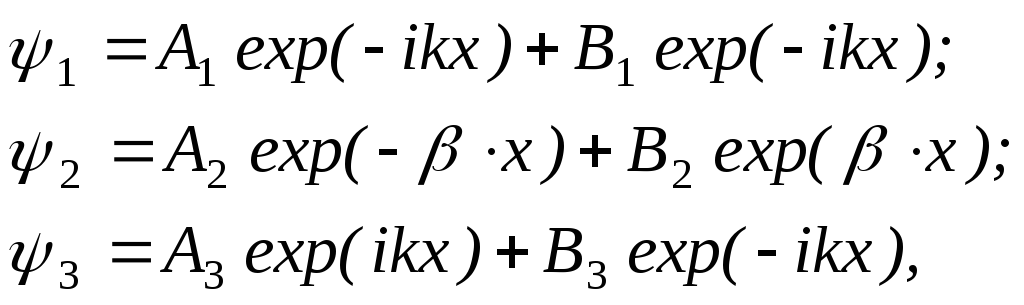
где

Факт «отражения» учитывается вторыми слагаемыми в выражениях (2). Эти члены можно интерпретировать как плоские волны, движущиеся в отрицательном направлении оси . В выражении (2) коэффициент, поскольку в области 3 отсутствует физическая причина для «отражения». Использовав граничные условия

получим следующие волновые функции в областях 1, 2 и 3 (с точностью до постоянного множителя ):

E

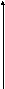
1 2 3 X a) l l 0 w б) X

Рис. 1

(3)

где .

Для дальнейшего анализа можно упростить выражение (3), приняв во внимание, что вероятность прохождения частиц сквозь потенциальный барьер невелика. Положив в (3)

получим

(4)

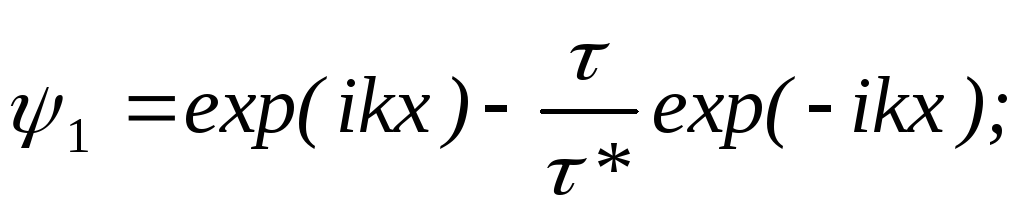
Анализ выражений (4) показывает, что частица с энергией , движущаяся слева в сторону потенциального барьера, может быть обнаружена как внутри барьера (область 2), так и справа от него (область 3). Количественно эффект туннелирования можно оценить, вычислив плотность вероятностиобнаружения частиц в каждой из областей пространства. Таким образом, получаем

(5)

Из выражения (5) видно, что вероятность туннельного прохождения частицей потенциального барьера существенно зависит от энергии частицы и ширины потенциального барьера. Качественные представления о виде функций (5) можно получить из рис.1,б. Вероятность туннелирования частиц принято характеризовать коэффициентом прохождения (коэффициентом прозрачности) потенциального барьера, который определяется отношением квадратов модулей волновой функции ψ₃ и первого слагаемого из ψ₁, описывающего падающую на барьер волну. Коэффициент прозрачности барьера описывается выражением

(6)

3.Туннельный эффект составляет физическую основу действия обширного класса полупроводниковых приборов – туннельных диодов (ТД). Принцип работы ТД можно пояснить с использованием представлений о зонной энергетической структуре твердого тела. В процессе образования твердого тела электронные энергетические уровни отдельных атомов из-за взаимодействия электронов смещаются и образуют энергетические полосы (разрешенные зоны), чередующиеся с зонами энергий, значений которых электроны принимать не могут (запрещенными зонами). Энергетическая ширина как разрешенной, так и запрещенной зоны имеет порядок ~10^-19Дж. Энергетический зазор между отдельными уровнями разрешенной зоны около 10^-41Дж, поэтому обычно считают, что энергетический спектр электронов внутри разрешенной зоны практически непрерывен. Наиболее сильно расщепляются энергетические уровнивалентных электронов, образуя так называемыевалентную зону и зону проводимости.

Многие электрофизические свойства твердых тел связаны с электронами в частично заполненных зонах, так как в пределах этих зон электроны могут изменять свою энергию под действием внешних факторов, и способны, в частности, участвовать в процессе электропроводности.

Вероятность заселения электронами энергетических уровней в зонах определяется статистикой Ферми-Дирака, описывающей энергетическое распределение частиц, подчиняющихся принципу Паули. Вероятность того, что состояние с энергией Е при температуре Т занято электроном, определяется функцией Ферми

Величину называютэнергией (уровнем) Ферми. Легко видеть, что при функция, если, и равна нулю, если(см. рис. 2а). При любой другой температуре энергия Ферми совпадает с энергией того уровня, вероятность заполнения которого равна 0,5. Если бы энергетические уровни в зоне были распределены равномерно, число электронов, имеющих энергию Е_i в небольшом интервале dE, определялось бы из функции Ферми (заштрихованная площадь на рис. 2,а). Однако вблизи дна зоны проводимости энергетические уровни расположены реже, чем в ее верхней части. Распределение энергетических уровней в зоне проводимости характеризуют функцией – плотностью энергетических состояний. С хорошим приближением считается, чтоимеет вид

(7)

где – масса (эффективная) электрона;Е_с – энергия, соответствующая дну зоны проводимости. Плотность заполнения электронами уровней энергетической зоны описывается функцией распределения

(8)

е

T=0

T>0

0

0,5

1,0

E_c

E_i

E_F

E

w

a)

n,w,D

E

n w D

E_F

E_m

б)

E_c

Рис. 2

е график изображен на рис.2,б.

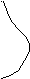
Общая концентрация электронов в зоне пропорциональна заштрихованной площади на рис.2,б. Аналогичные результаты справедливы и для материала с дырочной проводимостью, с тем отличием, что энергия отсчитывается от значения (энергии потолка валентной зоны) в сторону убывания.

4. При контакте материалов с различным типом электропроводности образуется переход. Если материалы относятся к вырожденным полупроводникам, при малой толщине перехода (10^-8м) возникают условия, благоприятствующие туннелированию носителей сквозь потенциальный барьер перехода. В вырожденных полупроводниках уровень Ферми находится не в запрещенной зоне, а смещен в полупроводникетипа в зону проводимости объединенную с так называемойпримесной зоной, образующейся из энергетических уровней доноров при их высокой концентрации (~ 10²⁴ – 10²⁶ м^-3). В вырожденном полупроводнике типа уровень Ферми находится в верхней части валентной зоны, объединенной с примесной зоной акцепторов.

E_F

E_V

E_F

E_c

“n” “p”

а)

E_c

E_F

E_F

E_V

“n” “p”

б)

“n” “p”

в)

E_c

E_F

E_V

E_F

Рис. 3

Процесс формирования вольт-амперной характеристики туннельного диода можно проследить по рис.3 и 4.

E_v

n(E)

P(E)

D(E)

E_c

E_m

E_F

E_F

D(E)

E

Рис. 4

Если напряжение на диоде равно нулю, ток через диод также равен нулю, так как переход электронов на заполненные уровни невозможен, а вероятность переходов слева и справа для электронов с энергией E_i >E_F. При приложении к диоду прямого напряжения (рис.3,б) энергетические уровни в области смещаются вниз в сравнении с уровнями вобласти; границы зон сближаются. Число переходов электронов изобласти вобласть увеличивается, так как большей плотности занятых состояний вобласти соответствует большая плотность свободных состояний («дырок») вобласти; одновременно уменьшается число переходов электронов изобласти вобласть (рис.4) до тех пор, пока не произойдет совпадение максимумов функций распределения (черные точки на рис.4); дальнейшее увеличение прямого напряжения вызывает уменьшение туннельного тока. По достижении напряжения(совпадение границ зоны проводимости и валентной) туннельные переходы прекращаются, так как против занятых электронами уровней находятся запрещенные энергетические состояния. Отличие от нуля тока(рис.5) и дальнейшее увеличение прямого тока по мере возрастания напряжения объясняются преодолением электронами потенциального барьера за счет теплового движения (см. описание к работе 3.06)

Зонная диаграмма туннельного диода при обратном смещении показана на рис.3,в.