- •Примеры решения типовых задач
- •Приведение квадратичных форм к каноническому виду
- •Раскрытие неопределенностей с помощью правила лопиталя
- •Разделяем переменные:
- •Операции над событиями
- •Вероятность того, что деталь находится только в одном ящике, равна
- •Числовые характеритстики случайных величин
- •Функции распределения
Приведение квадратичных форм к каноническому виду
Пример.Привести к каноническому виду квадратичную форму
Ф(х1, х2)
= 27![]() .
.
Коэффициенты: а11= 27, а12= 5, а22= 3.
Составим
характеристическое уравнение:
![]() ;
;
(27 - )(3 - ) – 25 = 0
2 - 30 + 56 = 0
1 = 2; 2 = 28;
![]()
Пример.Привести к каноническому виду уравнение второго порядка:
17x2+ 12xy+ 8y2– 20 = 0.
Коэффициенты
а11= 17, а12= 6, а22= 8.
А =![]()
Составим
характеристическое уравнение:
![]()
(17 - )(8 -) - 36 = 0
136 - 8- 17+2– 36 = 0
2- 25+ 100 = 0
1= 5,2= 20.
Итого:
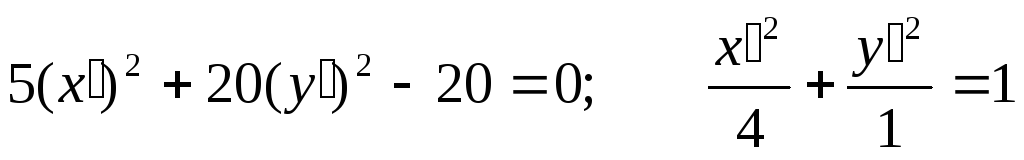 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.
![]()
Решение:Составим характеристическое уравнение
квадратичной формы![]() :
при
:
при![]()
![]()
Решив это уравнение, получим 1 = 2,2 = 6.
Найдем координаты собственных векторов:
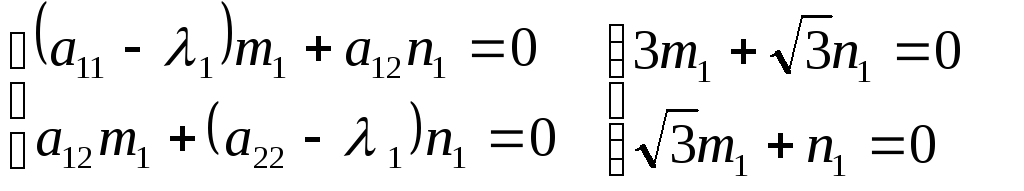 полагаяm1 = 1, получимn1
=
полагаяm1 = 1, получимn1
=
![]()
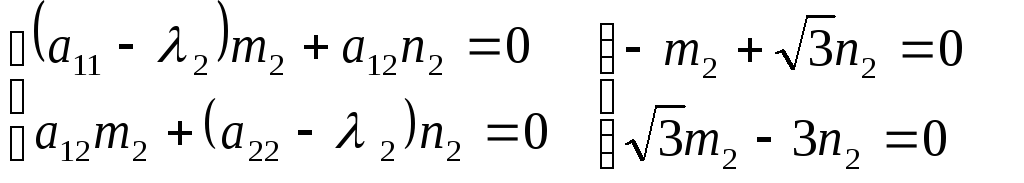 полагаяm2 = 1, получимn2
=
полагаяm2 = 1, получимn2
=
![]()
Собственные
векторы: ![]()
![]()
Находим координаты единичных векторов нового базиса.
![]()
Имеем следующее уравнение линии в новой системе координат:
![]()
Каноническое уравнение линии в новой системе координат будет иметь вид:
![]()

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.
![]()
Решение:Составим характеристическое уравнение
квадратичной формы![]() :
при
:
при![]()
![]()
Решив это уравнение, получим 1 = 1,2 = 11.
Найдем координаты собственных векторов:
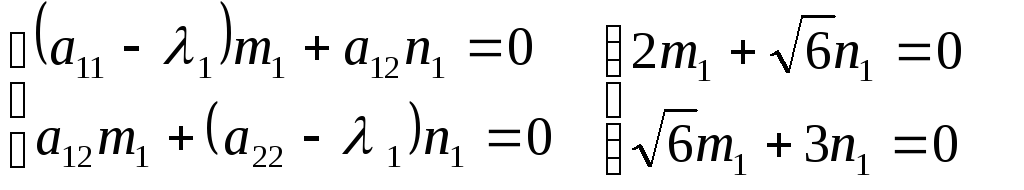 полагаяm1 = 1, получимn1
=
полагаяm1 = 1, получимn1
=
![]()
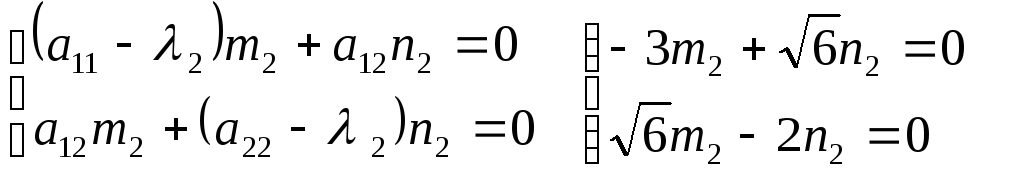 полагаяm2 = 1, получимn2
=
полагаяm2 = 1, получимn2
=
![]()
Собственные
векторы: ![]()
![]()
Находим координаты единичных векторов нового базиса.
![]()
Имеем следующее уравнение линии в новой системе координат:
![]()
Каноническое уравнение линии в новой системе координат будет иметь вид:
![]()

Пример.Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.
4ху + 3у2+ 16 = 0
Коэффициенты: a11= 0;a12= 2;a22= 3.
Характеристическое
уравнение:
![]()
Корни: 1= -1,2= 4.
Для 1= -1 Для2= 4
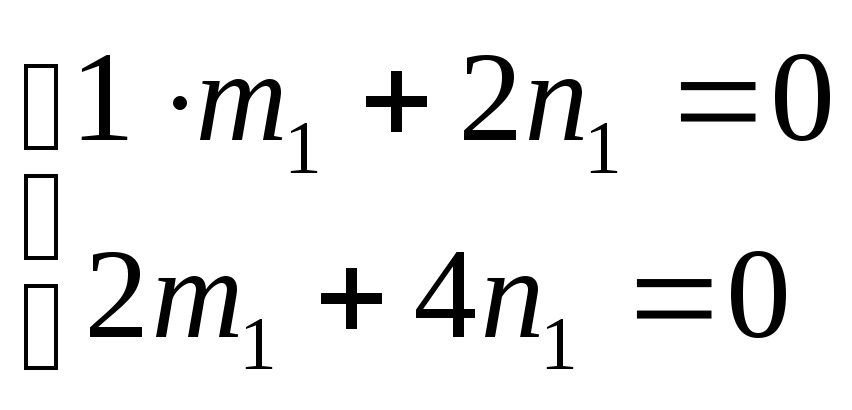

m1= 1;n1= -0,5;m2= 1;n2= 2;
![]() =
(1; -0,5)
=
(1; -0,5)
![]() =
(1; 2)
=
(1; 2)
![]()
![]()
![]()
![]()
Получаем:
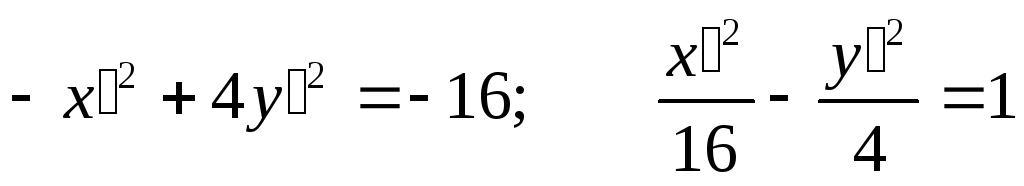 -каноническое уравнение гиперболы.
-каноническое уравнение гиперболы.
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Пример.Найти предел
![]()
Так как tg5x~ 5xиsin7x~ 7xпри х0, то, заменив функции эквивалентными бесконечно малыми, получим:
![]()
Пример.Найти предел![]() .
.
Так как 1 –
cosx=
![]() при х0, то
при х0, то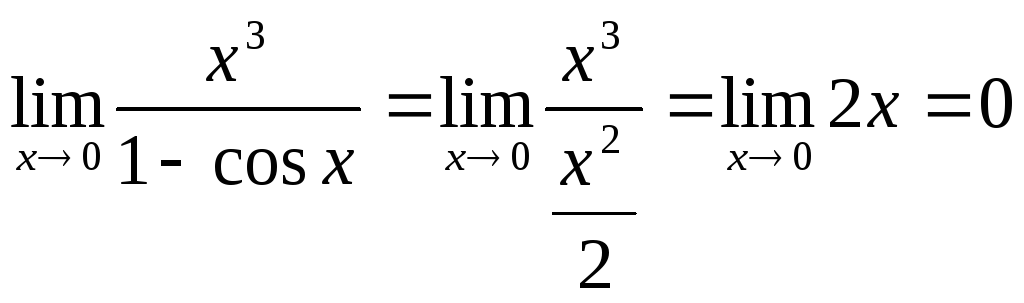 .
.
Пример.Найти предел![]()
Пример.Найти предел.
![]()
Пример. Найти предел.
![]()
Пример. Найти предел.
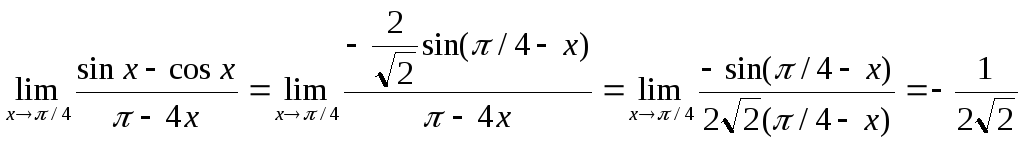
Пример. Найти предел.

Пример. Найти предел.

Пример.Найти предел![]() .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
x2 – 6x + 8 = 0; x2 – 8x + 12 = 0;
D = 36 – 32 = 4; D = 64 – 48 = 16;
x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6;
x2 = (6 – 2)/2 = 2 ; x2 = (8 – 4)/2 = 2;
Тогда
![]()
Пример.Найти предел.
![]() домножим числитель и знаменатель дроби
на сопряженное выражение:
домножим числитель и знаменатель дроби
на сопряженное выражение:
![]() =
=
=![]() .
.
Пример. Найти предел.
![]()
Пример.Найти предел
![]() .
.
Разложим числитель и знаменатель на множители.
x2 – 3x + 2 = (x – 1)(x – 2)
x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.
x 3– 6x2+ 11x– 6x- 1
3– 6x2+ 11x– 6x- 1
x3–x2x2– 5x+ 6
- 5x2+ 11x
- 5x2+ 5x
6x- 6
6x- 6 0
x2– 5x+ 6 = (x– 2)(x– 3)
Тогда
![]()
Пример.Найти предел.
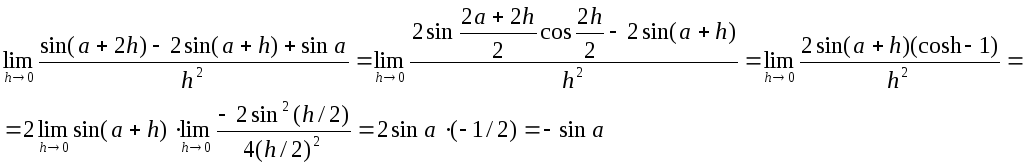
![]() - не определен, т.к. при стремлении х к 2
имеют место различные односторонние
пределы -∞ и +∞.
- не определен, т.к. при стремлении х к 2
имеют место различные односторонние
пределы -∞ и +∞.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Пример.Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)

не является непрерывной в любой точке х0.
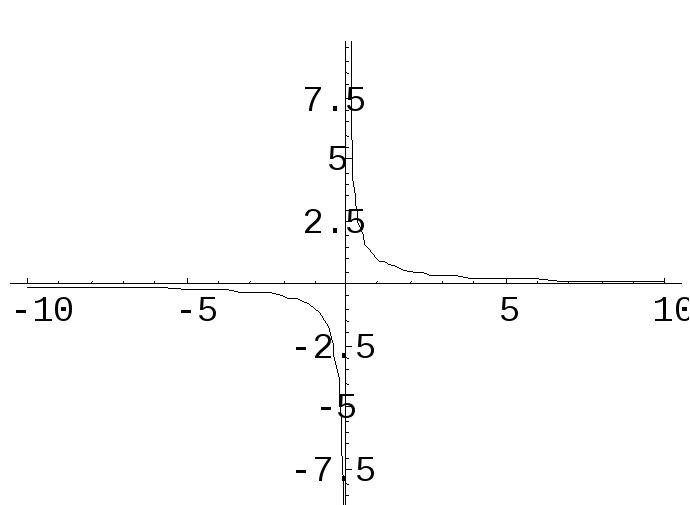
Пример.Функцияf(x)
=
![]() имеет в точке х0= 0 точку разрыва
2 – го рода, т.к.
имеет в точке х0= 0 точку разрыва
2 – го рода, т.к.
![]() .
.
![]()
Пример.f(x) =
![]()
Функция не
определена в точке х = 0, но имеет в ней
конечный предел
![]() ,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
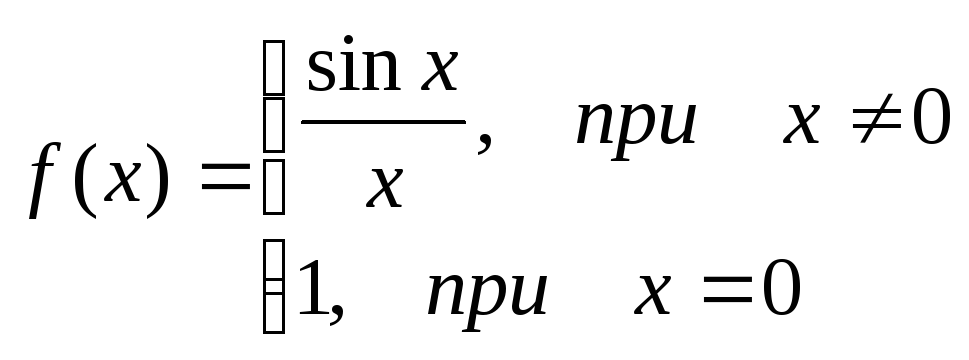
График этой функции:

Пример.f(x) =
![]() =
=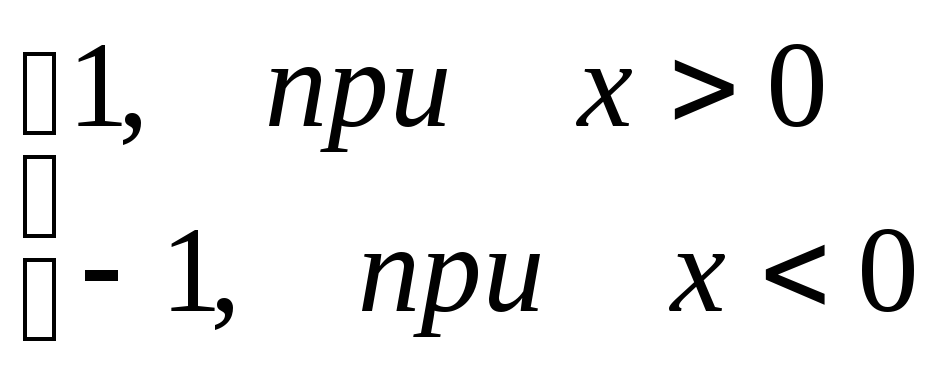
 y
y
1
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положивf(0) = 1, то функция будет непрерывна справа, если положитьf(0) = -1, то функция будет непрерывной слева, если положитьf(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
Пример.Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.



в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
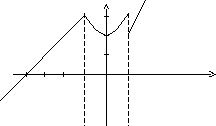 у
у
3
2
-4 -1 0 1 х
Пример.Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
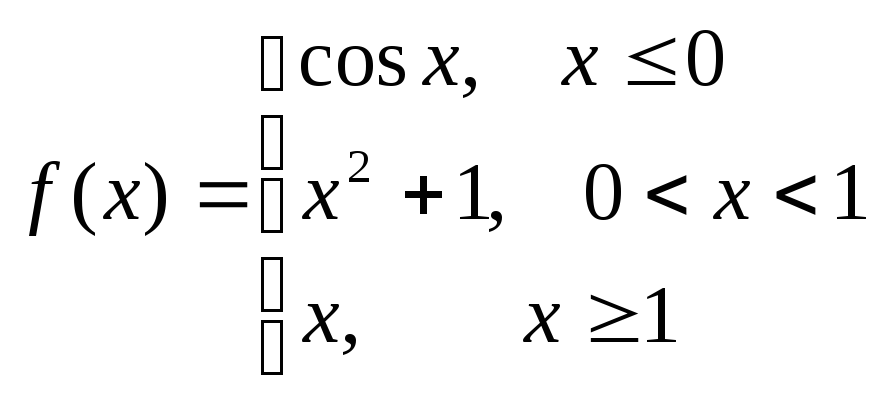

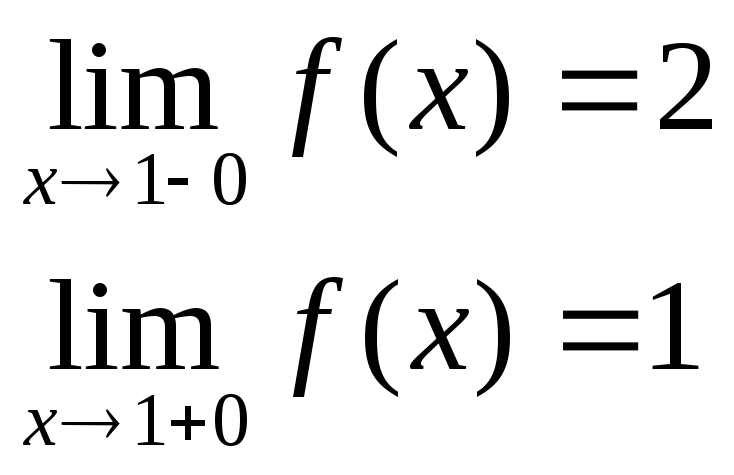
в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
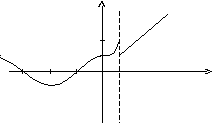
у
2
1
--/2 0 1x
БИНОМ НЬЮТОНА
Пример.В разложении![]() найти члены, содержащиех,
еслиk=3, p=2,
n=8, =9.
найти члены, содержащиех,
еслиk=3, p=2,
n=8, =9.
По фомуле
бинома Ньютона имеем:
![]()
C учетом числовых значений:
![]()
В принципе, можно написать разложение этого выражения в многочлен, определить коэффициеты либо непосредственно, либо из треугольника Паскаля (степень бинома сравнительно невелика), однако, делать это не обязательно, т.к. необходимо найти только член разложения, содержащийх9.
Найдем число
i, соответствующее
этому члену:
![]()
Находим:
![]()
Пример.В разложении![]() найти члены, содержащиеx.т=9, =6.
найти члены, содержащиеx.т=9, =6.
По обобщенной формуле бинома Ньютона получаем:
![]()
Для нахождения полного разложения необходимо определить все возможные значенияni, однако, это связано с громадными вычислениями. Однако, т.к. надо найти только члены, содержащиех6, тоn1= 6, а сумма всех четырех значенийправна 9. Значит, суммап2 + п3 + п4= 3.
Рассмотрим возможные значения этих величин:
|
n2 |
0 |
0 |
3 |
1 |
1 |
0 |
2 |
0 |
2 |
1 |
|
n3 |
0 |
3 |
0 |
2 |
0 |
1 |
1 |
2 |
0 |
1 |
|
n4 |
3 |
0 |
0 |
0 |
2 |
2 |
0 |
1 |
1 |
1 |
Искомые члены разложения:
![]()
![]()
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Пример.С помощью таблиц истинности проверить, являются ли эквивалентными формулыи.
![]()
Составим таблицы истинности для каждой формулы:
-
p
r
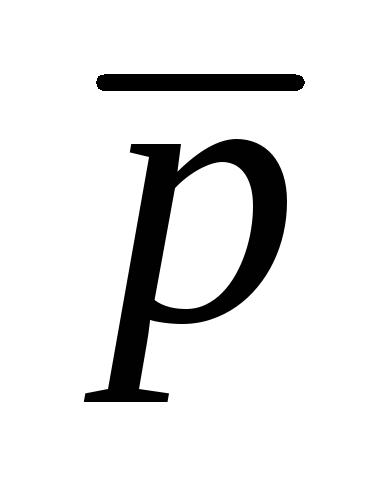
(pr)

И
И
Л
И
И
И
Л
Л
Л
И
Л
И
И
Л
Л
Л
Л
И
Л
Л
-
p
r


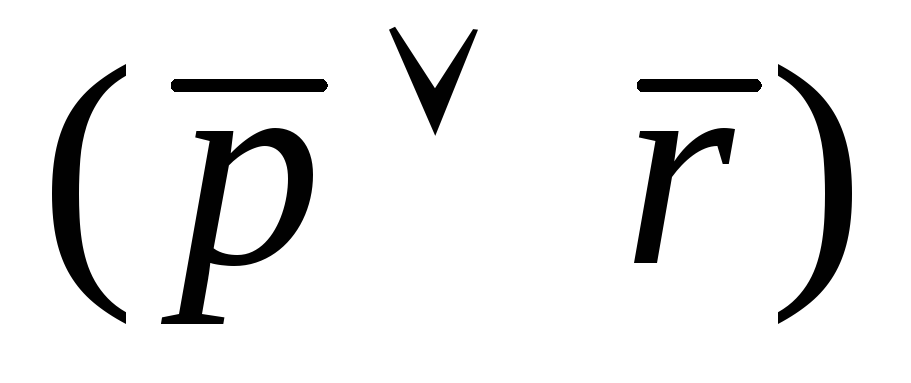
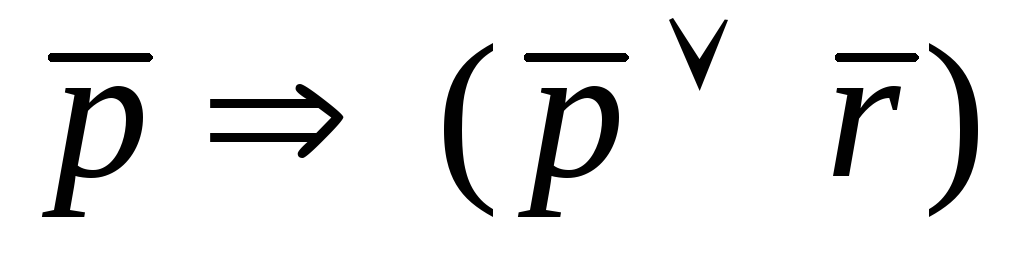
И
И
Л
Л
Л
И
И
Л
Л
И
И
И
Л
И
И
Л
И
И
Л
Л
И
И
И
И
Данные формулы не являются эквивалентными.
Пример.С помощью таблиц истинности проверить, являются ли эквивалентными формулыи.
![]()
Составим таблицы истинности для заданных формул.
-
p
q
r
pq
(pq)r
И
И
И
И
И
И
И
Л
И
И
И
Л
И
Л
И
И
Л
Л
Л
Л
Л
И
И
Л
И
Л
И
Л
Л
Л
Л
Л
И
И
И
Л
Л
Л
И
И
|
p |
q |
r |
pq |
qp |
(pq)(qp) |
(pq)(qp)r |
|
И |
И |
И |
И |
И |
И |
И |
|
И |
И |
Л |
И |
И |
И |
И |
|
И |
Л |
И |
Л |
И |
И |
И |
|
И |
Л |
Л |
Л |
И |
И |
И |
|
Л |
И |
И |
И |
Л |
И |
И |
|
Л |
И |
Л |
И |
Л |
И |
И |
|
Л |
Л |
И |
И |
И |
И |
И |
|
Л |
Л |
Л |
И |
И |
И |
И |
Из составленных таблиц видно, что данные формулы не равносильны.
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
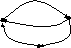
Пример.Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
x1
v1 x4 v2
x2
x3
v3
Составим матрицу смежности:
-
v1
v2
v3
v1
0
1
0
v2
1
0
1
v3
1
0
0
Т.е. - матрица смежности.
- матрица смежности.
Матрица инциндентности:
-
x1
x2
x3
x4
v1
-1
0
1
1
v2
1
-1
0
-1
v3
0
1
-1
0
Т.е.
Если граф имеет кратные дуги (ребра), то в матрице смежности принимается aij=k, гдеk– кратность дуги (ребра).
С помощью матриц смежности и инциндентности всегда можно полностью определеить граф и все его компоненты. Такой метод задания графов очень удобен для обработки данных на ЭВМ.
Пример.Задана симметрическая
матрицаQнеотрицательных
чисел. Нарисовать на плоскости графG(V,X),
имеющий заданную матицуQсвоей матрицей смежности. Найти матрицу
инциндентностиRграфаG. Нарисованть также орграф![]() ,
имеющий матрицу смежностиQ,
определить его матрицу инциндентности
С.
,
имеющий матрицу смежностиQ,
определить его матрицу инциндентности
С.
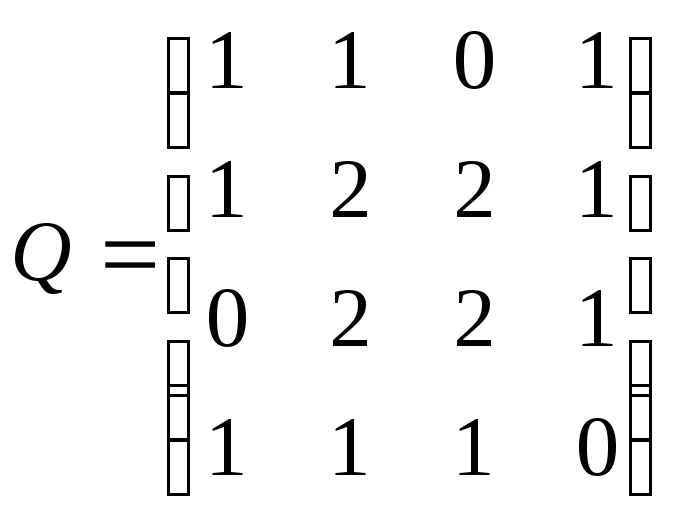
x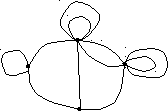 4
4
x3
v2
x2 x5
x6
x1 v1 v3 x7 x8
x10
x11x9
v4
Составим матрицу инциндентности:
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
|
v1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
v2 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
v3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
v4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
Итого:

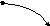
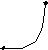
Построим теперь ориентированный граф с заданной матрицей смежности.
x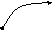


 4
4
x5


 v2
v2


 x2x7
x2x7

 х3x6
х3x6

 x1v1 х8v3x10x11
x1v1 х8v3x10x11
х9
х17х15x14
x16х13x12
v4
Составим матрицу инциндентности для ориетированного графа.
Элемент матрицы равен 1, если точка является концом дуги, -1 – если началом дуги, если дуга является петлей, элемент матрицы запишем как 1.

ПРОИЗВОДНАЯ
Пример.Найти производную функции![]() .
.
Сначала
преобразуем данную функцию:
![]()
![]()
Пример.
Найти производную функции![]() .
.
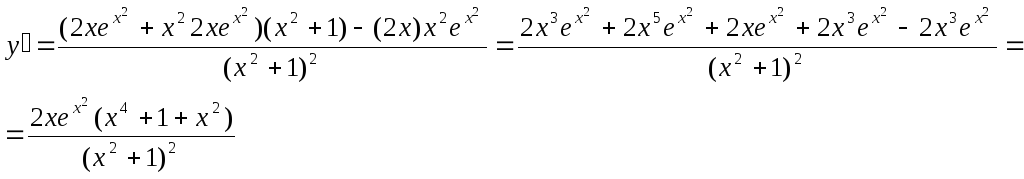
Пример.
Найти производную функции![]()
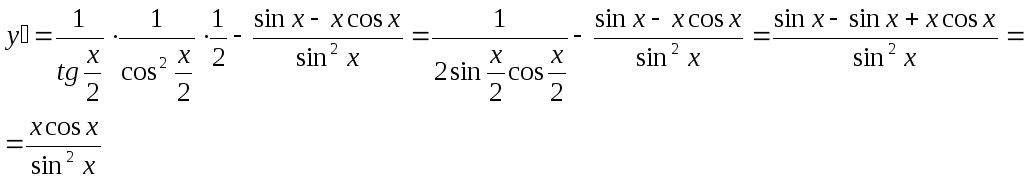
Пример.Найти производную функции![]()
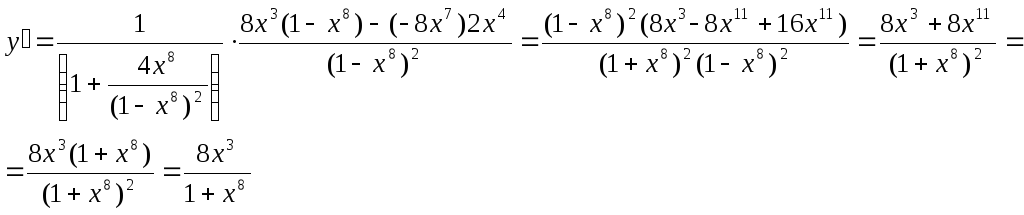
Пример.Найти производную функции![]()