3.4. Уравнение движения автомобиля

Сила тяги автомобиля (Р_р), полученная с помощью двигателя, расходуется на преодоление сопротивлений движению и придание автомобилю ускорения. Учитывая это, составим из условия равенства внешних и внутренних сил, действующих на автомобиль, уравнение движения автомобиля:

Р_р = Р_f  P_i + P_w  P_j, (3.17)

где P_f, P_i, P_w, P_j – описанные ранее виды сопротивлений движению автомобиля.

Сформируем в левой части члены уравнения, зависящие в основном от скорости движения и характеризующие динамические качества автомобиля. В правой части оставим составляющие, описывающие дорожные условия (дорожные сопротивления). Подставив значения сопротивлений, определенные ранее (п. 3.3), получим уравнение:

Р_р = . (3.18)

Академик Е.А. Чудаков предложил характеризовать тяговые (динамические) возможности автомобиля динамическим фактором – разницей между силой тяги на ведущих колесах и сопротивлением воздушной среды, отнесенной к единице веса автомобиля. После преобразования формулы (3.18) получим зависимость:

. (3.19)

Из которой следует, что динамический фактор – это избыточная удельная сила тяги, которая может быть использована на преодоление дорожных сопротивлений () и придание автомобилю ускорения (j).

Сила тяги и сопротивление воздушной среды в процессе движения автомобиля не остаются постоянными, а изменяются с изменением скорости. Поэтому величина динамического фактора также изменяется в зависимости от скорости. График зависимости динамического фактора от скорости при полной нагрузке на автомобиль, по предложению академика Е.А. Чудакова, назвали динамической характеристикой (рис. 3.6).

Такие графики используются в России как основные при всех тяговых расчетах на автомобильных дорогах (определение максимальных продольных уклонов, преодолеваемых автомобилями; величины скорости, развиваемой автомобилями на подъемах и т.д.).

Возможность приложения максимальных тяговых усилий, которые характеризуют динамические характеристики, зависит от сцепления колеса автомобиля с покрытием, поэтому для проверки реализации тяговых возможностей автомобиля строят графики динамических характеристик по сцеплению (D_сц). Их определяют, исходя из того, что

Р_р = G_сц·, (3.20)

тогда

. (3.21)

Совмещая графики динамических характеристик и графики динамических характеристик по сцеплению, определяют возможную скорость движения автомобиля в зависимости от сцепных качеств покрытия.

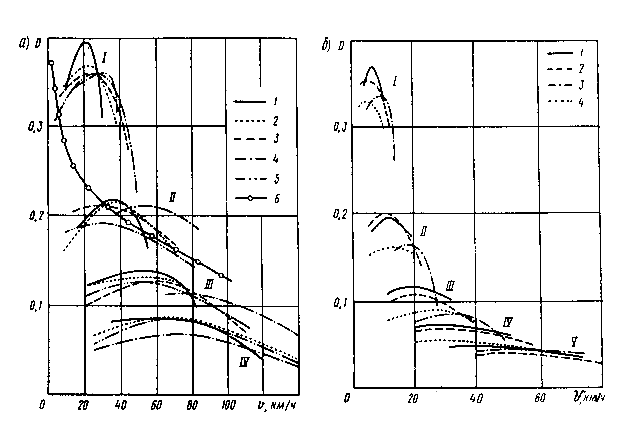
Рис. 3.6. Примеры графиков динамических характеристик автомобилей:

алегковых автомобилей различных марок (1, 2, 3, 4, 5, 6);б грузовых автомобилей различных марок (1, 2, 3, 4)

3.5. Торможение и тормозной путь автомобиля

В случае необходимости остановки автомобиля водитель пользуется торможением, которое может осуществляться следующими способами:

• отключение сцепления и последующее торможение осуществляется тормозными колодками о тормозной барабан. Этот способ наиболее эффективен на сухих шероховатых покрытиях;

• сцепление оставляется включенным на холостом ходу. После движения некоторое время в таком состоянии и снижения в результате этого скорости, начинается торможение тормозными колодками;

• на затяжных спусках торможение может осуществляться двигателем путем последовательного переключения на пониженные передачи. В этом случае энергия гасится трением: поршней двигателя о стенки цилиндров, подшипников, коленчатого вала и т.д., оно возникает в результате того, что ведущие колеса вращают вал отключенного двигателя.

Для определения требований к элементам дорог необходимо знать тормозной путь автомобиля. Его определяют по первому способу торможения. Рассмотрим для этого уравнение движения автомобиля. При отключенном двигателе (Р_р = 0) движущей силой будет выступать сила инерции. Тогда уравнение движения автомобиля будет иметь вид:

, (3.22)

где Р_т – тормозная сила, величина которой определяется выражением:

, (3.23)

где P_T – тормозная сила; – коэффициент тормозной силы, равный отношению суммы тормозных сил, возникающих на всех колесах, к весу автомобилей; -вес автомобиля.

Предельная величина принимается равным коэффициенту продольного сцепления , т.к. при большем тормозном усилии начинается проскальзывание заторможенных колес и эффект торможения снижается.

Путь, пройденный автомобилем за период полного торможения, определяют по формуле равномерно замедленного движения: V = , где - тормозной путь;V – скорость в начале торможения; -абсолютное значение отрицательного ускорения при торможении.

Отсюда:

. (3.24)

Тогда после подстановки выражения (3.24) в уравнение (3.22) и некоторых преобразований получим зависимость, характеризующую тормозной путь (S_т)

S_т = , (3.25)

где V – скорость в начале торможения, м/сек.

При этом сделаны следующие допущения:

• Р_w принято равным 0, т.к. при резком снижении скорости величина сопротивления воздуха довольно мала и не оказывает существенного влияния на получаемые результаты;

•   1, что несколько упрощает расчеты и дает дополнительный запас с точки зрения обеспечения безопасности движения.

Следует иметь ввиду, что из-за неточности регулировки тормозов и неравномерности распределения тормозного усилия между колесами теоретическая величина пути торможения, определяемая зависимостью (3.25), практически реализуется очень редко. Поэтому по предложению проф. Д.П. Великанова в зависимость (3.25) вводится коэффициент эффективности торможения (k_э). Тогда

S_т = . (3.26)

По данным многочисленных наблюдений установлено, что для легковых автомобилей = 1,2, а для грузовых и автобусов= 1,31,4.

При расчетах элементов автомобильных дорог для большей безопасности вводится понятиерасчетного тормозного пути (), который определяется по схеме торможения перед препятствием на дороге (рис. 3.7) и описывается зависимостью (3.27).

Рис. 3.7. Схема к определению расчетного тормозного пути

, (3.27)

где L₁ – путь проходимый автомобилем за время реакции водителя; L₂ = S_т – тормозной путь; L_з – расстояние запаса (зазор безопасности).

Время реакции водителя колеблется в пределах от одной до нескольких секунд в зависимости от большого числа факторов. Для расчетов по зависимости (3.27) время реакции водителя принимается равным 1с. Расстояние запаса принимается равным длине автомобиля (L_з = L_авт), тогда уравнение (3.27) будет иметь вид:

. (3.28)