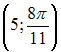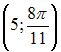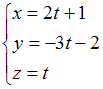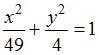Аналитическая геометрия
.docxАналитическая геометрия
Тема: Полярные координаты на плоскости
1)Точка
задана
в прямоугольной системе координат.
Тогда ее полярные координаты равны …
|
|
,
2)
Полярные
координаты точки, симметричной точке
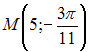относительно
полюса, равны …
|
|
|
|
|
3)
В полярной системе координат кривая
определяет …
|
|
|
|
окружность |
4)
Полярные
координаты точки, симметричной точке
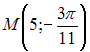относительно
полюса, равны …
|
|
|
|
|
5)
Точка
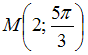задана
в полярной системе координат. Тогда ее
прямоугольные координаты равны …
|
|
|
|
|
,
6).
В полярной системе координат кривая
определяет
…
|
|
|
|
окружность |
Тема: Поверхности второго порядка
2)
Уравнение
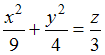в
пространстве определяет …
|
|
|
|
параболоид |
3)
Вершина
конуса
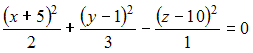имеет
координаты …
|
|
|
|
|
4)
Уравнение
сферы с центром в точке
и
радиусом
имеет
вид …
|
|
|
|
|
5).
Уравнение сферы с центром в точке
и
радиусом
имеет
вид …
|
|
|
|
|
Тема: Прямая на плоскости
1)Дано
уравнение прямой
.
Тогда уравнение этой прямой «в отрезках»
имеет вид …
|
|
|
|
|
||||||||||||||||
|
2)
Угловой
коэффициент прямой, заданной уравнением
3)
Общее уравнение прямой, проходящей
через точку
4).
Угловой коэффициент прямой, заданной
уравнением
5)
Прямая проходит через точки
|
|
|
|
,
равен …
параллельно
прямой
имеет
вид …
,
равен …
и
.
Тогда общее уравнение этой прямой
имеет вид …
Тема: Прямая и плоскость в пространстве
1)Даны
точки
и
.
Тогда уравнение плоскости, проходящей
через точку
перпендикулярно
вектору
,
имеет вид …
|
|
|
|
|
2)
Прямая
проходит через точку
параллельно
прямой
.
Тогда уравнение этой прямой имеет вид …
|
|
|
|
|
||||
|
3)
Параметрические
уравнения прямой, проходящей через
точку
|
|
|
|
параллельно
вектору
имеют
вид …
4)
Каноническое
уравнение прямой, проходящей через
точки
и
имеет
вид …
|
|
|
|
|
5)
Дано общее уравнение плоскости
.
Тогда уравнение этой плоскости «в
отрезках» имеет вид …
|
|
|
|
|
Тема: Прямоугольные координаты на плоскости
1)Расстояние
между точками 
и
равно …
|
|
|
|
5 |
2)
Точка
симметрична
точке
относительно
оси ординат. Тогда расстояние между
точками
и
равно …
|
|
|
|
4 |
3)
Даны точки
,
,
и
.
Тогда линии, заданной уравнением
,
принадлежит точка …
|
|
|
|
|
4)
Даны
точки
и
.
Тогда координаты середины отрезка
равны …
|
|
|
|
|
5).
Даны точки
и
.
Тогда координаты середины отрезка
равны
…
|
|
|
|
|
Тема: Кривые второго порядка
1)Уравнение
окружности с центром в точке
и
радиусом
имеет
вид …
|
|
|
|
|
2)
Эксцентриситет
гиперболы
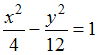равен …
|
|
|
|
2 |
3)
Уравнение
окружности с центром в точке
и
радиусом
имеет
вид …
|
|
|
|
|
4) Фокусы эллипса лежат на оси абсцисс симметрично относительно начала координат, а длины полуосей равны соответственно 7 и 2. Тогда каноническое уравнение эллипса имеет вид …
|
|
|
|
|
5)
Уравнение
параболы имеет вид
.
Тогда директриса задается уравнением …
|
|
|
|
|
