
Математическая статистика
.docxМатематическая статистика
Тема: Точечные оценки параметров распределения
1)
Из генеральной совокупности извлечена
выборка объема
![]() :
:
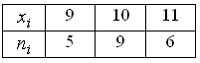 Тогда
несмещенная оценка математического
ожидания равна …
Тогда
несмещенная оценка математического
ожидания равна …
|
|
|
|
|
2) Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 7, 8, 10. Тогда несмещенная оценка математического ожидания равна …
|
|
|
|
|
3) В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 12, 14. Тогда выборочная дисперсия равна …
|
|
|
|
|
4)
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
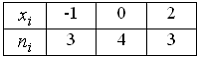 Тогда
выборочная дисперсия равна …
Тогда
выборочная дисперсия равна …
|
|
|
|
|
5)
Из генеральной совокупности извлечена
выборка объема
![]() :
:
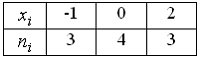
Тогда выборочная дисперсия равна …
|
|
|
|
|
Тема: Проверка статистических гипотез
1)Основная
гипотеза имеет вид
![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …
|
|
|
|
|
2) Двусторонняя критическая область может определяться из соотношения …
|
|
|
|
|
3)
Основная
гипотеза имеет вид
![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …
|
|
|
|
|
4) Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
5) Двусторонняя критическая область может определяться из соотношения …
|
|
|
|
|
6) Правосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
Тема: Характеристики вариационного ряда
1)Медиана вариационного ряда 2, 3, 3, 4, 5, 6, 8, 10, 12 равна …
|
|
|
|
|
2) Медиана вариационного ряда 1, 3, 4, 5, 5, 7, 9, 11, 13, 14 равна …
|
|
|
|
|
3) Размах варьирования вариационного ряда 1, 2, 4, 4, 6, 8, 9, 10,12, 15 равен …
|
|
|
|
14 |
4)
Мода вариационного ряда 1, 2, 2, 3, 4, 4,
![]() ,
7, 7, 8, 9 равна 4. Тогда значение
,
7, 7, 8, 9 равна 4. Тогда значение
![]() равно
…
равно
…
|
|
|
|
|
5) Мода вариационного ряда 1, 3, 3, 4, 5, 5, 5, 7, 7, 8, 9 равна …
|
|
|
|
|
Тема: Статистическое распределение выборки
1)Статистическое
распределение выборки имеет вид
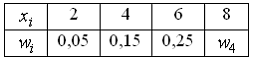 Тогда
значение относительной частоты
Тогда
значение относительной частоты
![]() равно …
равно …
|
|
|
|
|
2)
Из
генеральной совокупности извлечена
выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
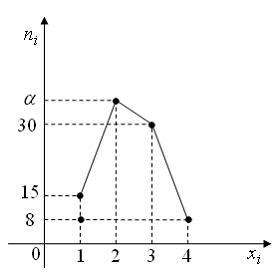 Тогда
значение параметра
Тогда
значение параметра
![]() равно …
равно …
|
|
|
|
47 |
3)
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
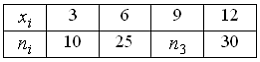 Тогда
относительная частота варианты
Тогда
относительная частота варианты
![]() равна …
равна …
|
|
|
|
|
4)
Статистическое
распределение выборки имеет вид
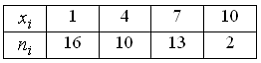 Тогда
объем выборки равен …
Тогда
объем выборки равен …
|
|
|
|
41 |
5)
Из
генеральной совокупности извлечена
выборка объема
![]() ,
гистограмма частот которой имеет
вид:
,
гистограмма частот которой имеет
вид:
 Тогда
значение параметра a
равно …
Тогда
значение параметра a
равно …
|
|
|
|
24 |
6)
Из генеральной совокупности извлечена
выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
значение параметра
Тогда
значение параметра
![]() равно
…
равно
…
|
|
|
|
47 |
Тема: Элементы корреляционного анализа
1)Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочный коэффициент регрессии
равен …
.
Тогда выборочный коэффициент регрессии
равен …
|
|
|
|
|
2)
Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочное среднее признака
.
Тогда выборочное среднее признака
![]() равно …
равно …
|
|
|
|
|
3)
Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочное среднее признака
.
Тогда выборочное среднее признака
![]() равно …
равно …
|
|
|
|
|
4)
Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
5)
Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
6)
Выборочное уравнение прямой линии
регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
Тема: Интервальные оценки параметров распределения
1)Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
|
|
|
|
|
2)
Точечная
оценка математического ожидания
нормально распределенного количественного
признака равна
![]() Тогда
его интервальная оценка с точностью
Тогда
его интервальная оценка с точностью
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
3)
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
|
|
|
|
|
4)
Точечная
оценка среднего квадратического
отклонения нормально распределенного
количественного признака равна
![]() .
Тогда его интервальная оценка может
иметь вид …
.
Тогда его интервальная оценка может
иметь вид …
|
|
|
|
|
5)
Точечная оценка математического ожидания
нормально распределенного количественного
признака равна
![]() .
Тогда его интервальная оценка может
иметь вид …
.
Тогда его интервальная оценка может
иметь вид …
|
|
|
|
|

































