2. Решение типовой задачи

К стальному валу приложены моменты: M₁= 1000 Н·м; М₂= 1200 Н·м; М₃= 1500 Н·м; М₄= 2000 Н·м (рис. 2.3).

Построить эпюры крутящих моментов и углов закручивания, определить наибольший относительный угол закручивания.

Рис. 2.3. Демонстрация построения эпюр крутящего момента и угла закручивания при кручении

Исходные данные для решения задачи: а = 1 м; b = 1,5 м; с = 1,2 м; = 50 МН/м².

Решение.

1) Построим эпюру крутящих моментов. Для этого на каждом участке вала проведем сечения (1 – 4) и запишем уравнения крутящих моментов как алгебраические суммы внешних моментов, лежащих справа от сечения:

Участок BE: М_х1= М₄= 2000 Н·м (момент М₄в уравнении записан со знаком «+», так как со стороны проведенного сечения 1 вращение момента М₄направлено по часовой стрелке).

Участок ЕD: М_х2= М₄– М₃; М_х2 = 2000 – 1500 = 500 (Н·м).

Участок DC: М_х3= М₄ – М₃– М₂; М_х3= 2000 – 1500 – 1200 = – 700 (Н·м).

Участок CA: М_х4= М₄– М₃– М₂ – М₁; М_х4= 2000 – 1500 – 1200 – 1000 = = – 1700 (Н·м).

Эпюра М_хпредставлена на рис. 2.3. Проверить правильность построения эпюры можно следующим образом: в том сечении, где приложен крутящий момент, эпюра М_хвсегда имеет скачок на величину момента. Из эпюры следует, что реактивный момент в заделке М_А= 1700 Н·м.

При заданном значении определяем диаметр вала из условия проч-ности (2.3) по формуле (2.4).

Наибольшее значение М_хопределяем из эпюры крутящих моментов по абсолютной величине: M_{x max}= 2000 Н·м.

Тогда из уравнения (2.4) следует:

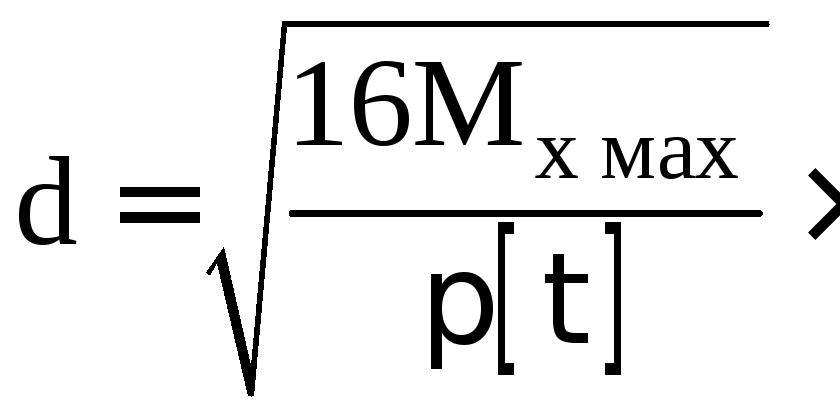(2.6)

После подстановки данных в формулу (2.6) получим:

= 0,014 (м).

Из предложенных стандартом профилей круглого сечения (30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм) выбираем ближайшее большее значение d – 30 мм.

2) Построим эпюру углов закручивания.

Левое закрепленное сечение А не поворачивается, поэтому = 0.

Углы поворота остальных сечений находим по формуле (2.5), предварительно вычислив величину и жесткость вала:

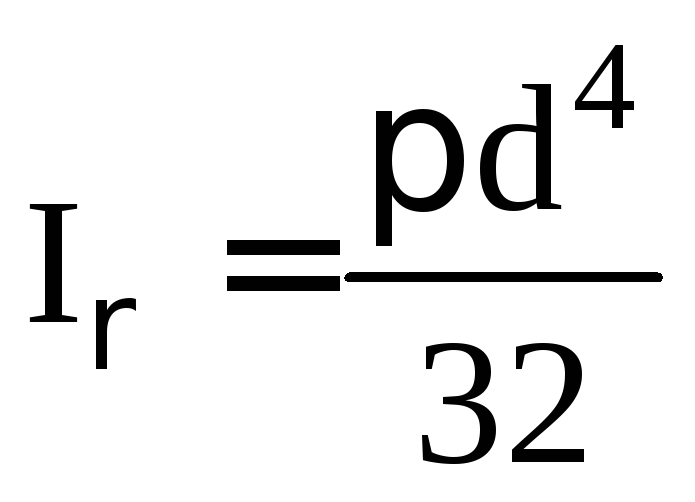. (2.7)

После подстановки данных получим: (м⁴);(Н·м²).

Определим угол закручивания на участках СА, DA, EA и BA:

; (2.8)

; (2.9)

; (2.10)

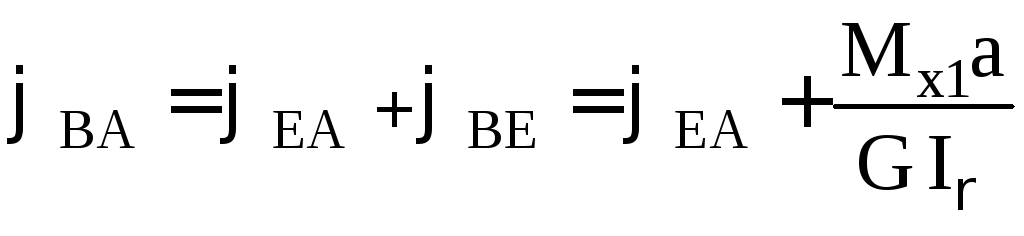(2.11)

После подстановки значений получим:

(рад);(рад);(рад);(рад).

Отложив найденные значения углов поворота сечений в точках, соответствующим концам рассматриваемых участков, соединим ординаты прямыми линиями, так как согласно формуле(2.5) углы закручивания прямо пропорциональны длине валаL. Полученный график и есть эпюра.

Определим наибольший относительный угол закручивания (на один погонный метр) по формуле:

. (2.12)

Наибольший относительный угол закручивания будет на участке BE:

;(рад/м).

Расчет на кручение имеет свои особенности. Построение эпюры М_хдля такого вала принципиально не отличается от предыдущего решения, однако следует иметь в виду, что подшипники позволяют валу свободно вращаться и в них реактивные моменты не возникают.

Необходимо также учитывать, что все сечения такого вала вращаются. Для построения эпюры углов закручивания в этом случае условно принимают за неподвижное крайнее левое сечение или правое. Расчетная схема вала, расположенного в подшипниках, эпюры М_хиприведены на рис. 2.4. В качестве неподвижного принято левое сечение.

Рис. 2.4 Демонстрация построения эпюр крутящего момента и угла закручивания при кручениивала, расположенного в подшипниках