2.4. Магнитное поле соленоида

С учетом обозначений на рис. 8, на основе уравнения (11) выражение для поля Н (оно направлено вдоль оси соленоида) запишем в виде:

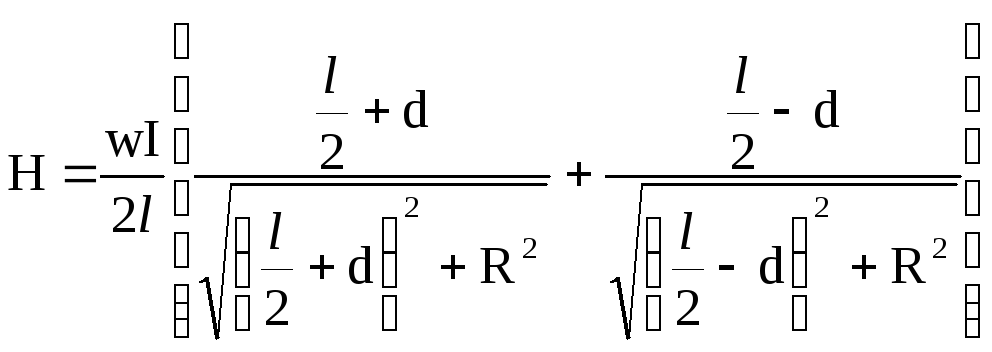. (17)

с

Рис. 8. Поле на оси соленоида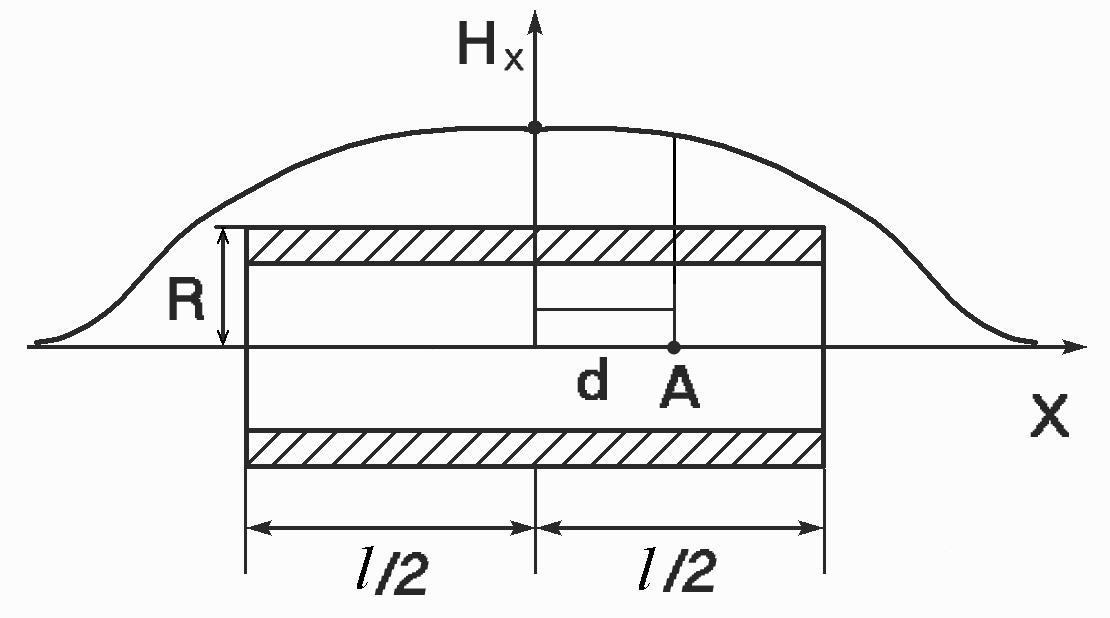

оотношение (17) применяется для расчета при проведении магнитной дефек-тоскопии, так как соленоиды широко исполь-зуются для намагничивания деталей.

Часто пользуются упрощенным вариантом выражения (17), считая соленоид бесконечно длинным, т. е., принимая >>R, имеем:

. (18)

Поле соленоида пропорционально току Iи отношению числа витков к длине соленоида, которое называютпостоянной соленоида.

В центре соленоида

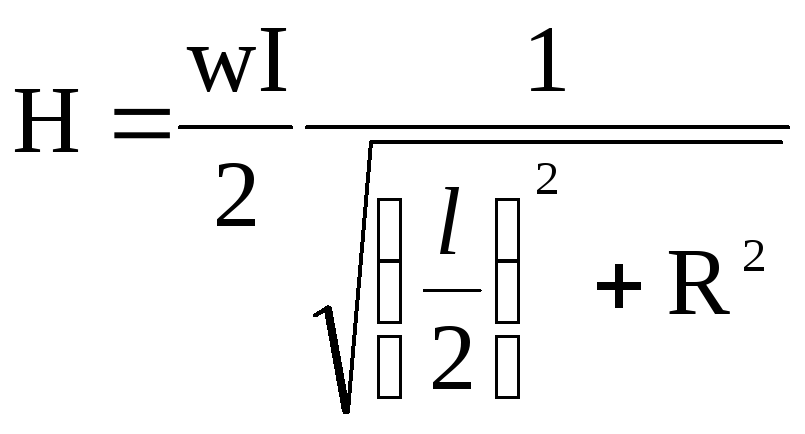, (19)

у края соленоида

. (20)

Если при этом l >> R, то, т. е. на краю длинного соленоида поле в два раза меньше, чем в середине. ПриR>> lвыражение (17) переходит в уравнение (15) с соответствующим числом витков.

Как видно из рис. 8, поле будет однородным лишь внутри и вблизи центра соленоида. Приближаясь к его краям, силовые линии начинают расходиться, и напряженность поля падает. Снаружи, например, у правого конца, силовые линии «загибаются назад», рассеиваются и на входе слева сгущаются.

2.5. Магнитное поле проводника конечного сечения

В практике магнитной дефектоскопии для контроля осесимметричных деталей или деталей в форме тел вращения часто применяют циркулярное намагничивание путем пропускания тока непосредственно вдоль оси детали. При этом поле (см. рис. 6, б) в некоторой точке вне цилиндра, удаленной на расстояние rот центра цилиндра, рассчитывается по формуле (13). Так как поле внутри цилиндра создается током, где плотность тока, а, то дляr<<r₀поле определяется как, и оно, как и следовало ожидать, совпадает с полем, рассчитанным по формуле (14).

Таким образом,

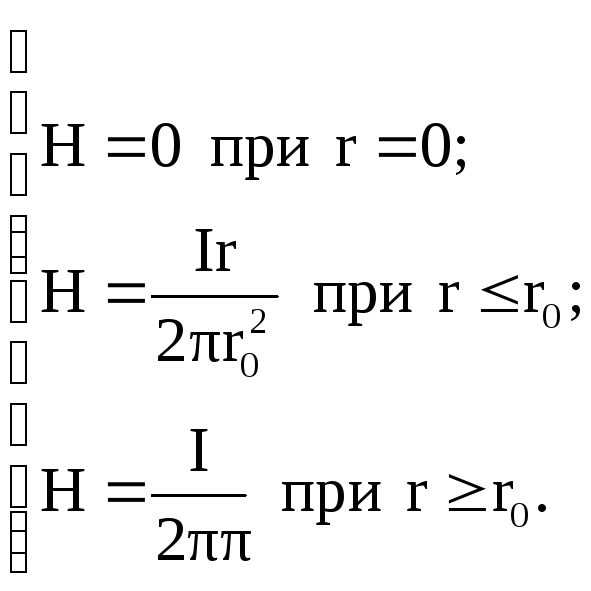(21)

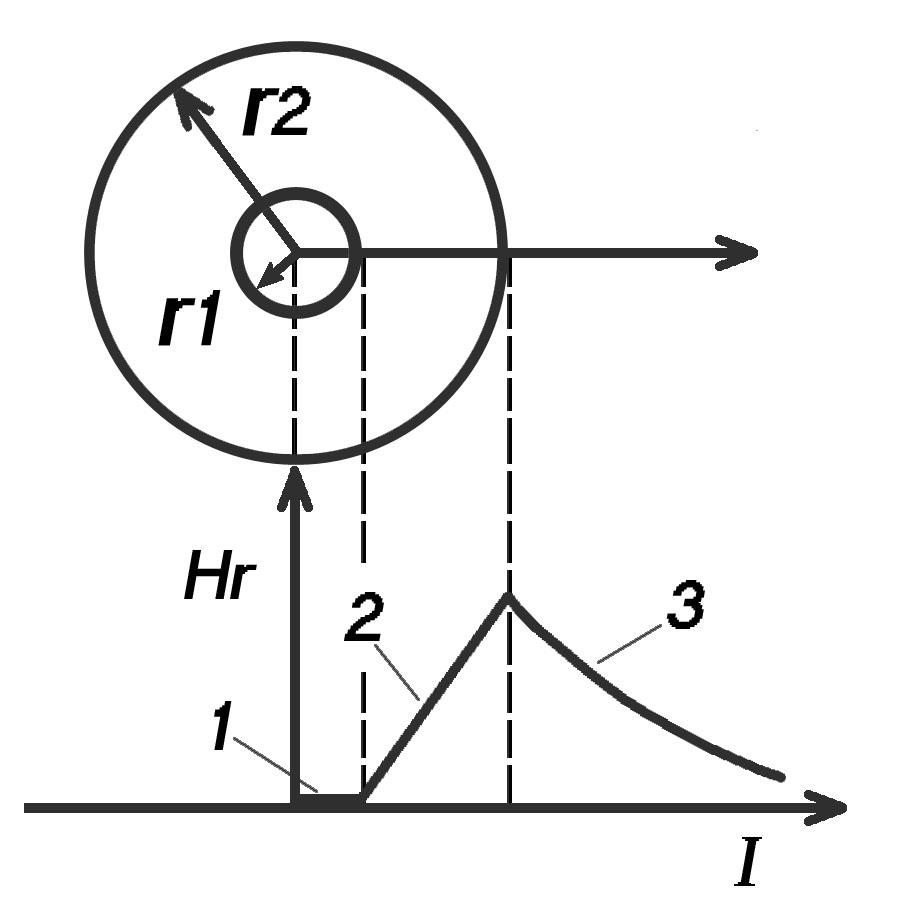
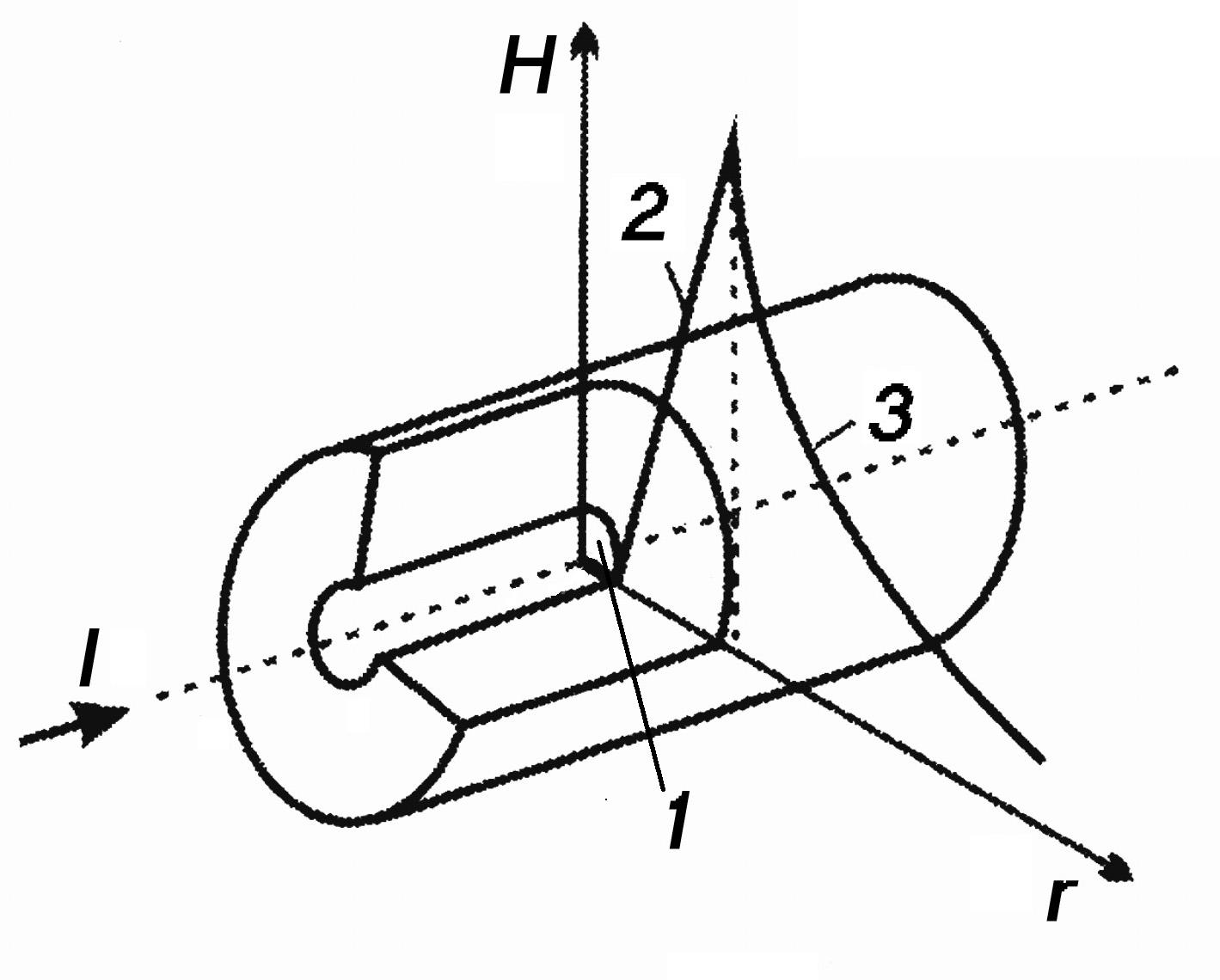
2.6. Магнитное поле тока, текущего по трубе

Аналогичные рассуждения дают в данном случае следующие результаты по участкам 1 – 3 (рис. 9):

(22)

а б

Рис. 9. Поле тока, текущего по трубе

3. Магнетизм и намагничивание

Носители магнетизма в металле – элементарные электрические токи в атомах (гипотеза Ампера), создаваемые вращением электронов вокруг ядра (рис. 10, а), прецессионным движением (качанием) электронных орбит (рис. 10, б) и вращением электронов вокруг своей оси – спином электрона (рис. 10, в), который вносит наибольший вклад в образование магнитного поля в атоме.

Элементарные токи в каждом атоме формируют атомные магнитные моменты , которые, складываясь между собой, образуют магнитное поле атома и, в конечном счете, вещества в целом. Однако большинство веществ не проявляет магнитных свойств, так как магнитные моменты их атомов направлены произвольно и взаимно компенсируют друг друга, т. е. размагничиваются уже в небольшом своем объеме.

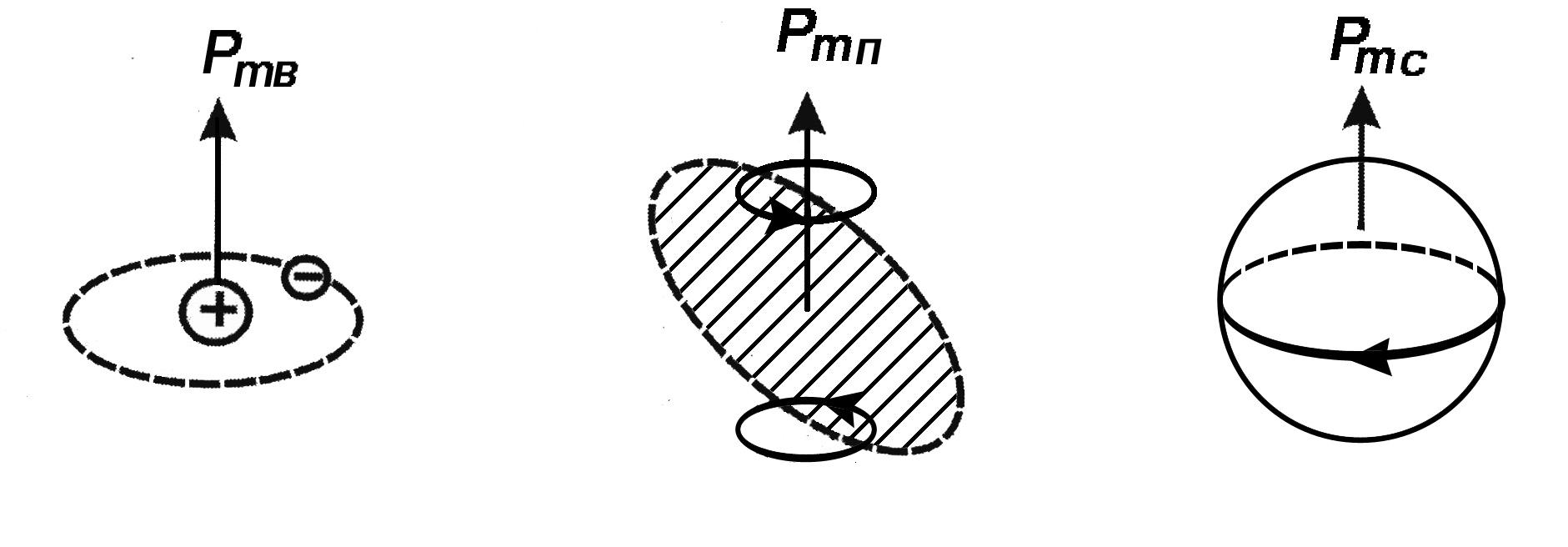
а б в

Рис. 10. Магнитные моменты в атоме, формируемые элементарными токами:

а – движением электрона вокруг ядра; б – прецессией электронной

орбиты; в – вращением электрона вокруг своей оси

Существуют материалы с высокой способностью к намагничиванию – ферромагнетики. Их в природе насчитывается немного. Главный среди них – железо. На его основе с добавками никеля, кобальта, вольфрама и алюминия созданы все ферромагнитные сплавы. У них совершенно особая структура. Даже если нет внешнего магнитного поля, моменты миллионов соседних атомов самопроизвольно выстраиваются параллельно друг другу, образуя микроскопические области, так называемые домены – идеальные магниты в миниатюре. Это крошечные, в обычном представлении, но огромные по сравнению с размерами атомов области. Число атомов в них составляет порядка 10¹⁵, а размеры в поперечнике – около 10 мкм. Все магнитные моменты атомов внутри домена ориентированы одинаково, т. е. эта область намагничена до насыщения и представляет собой относительно сильный постоянный магнит. Она характеризуется магнитным моментом домена.

Если нет внешнего магнитного поля, то магнитные моменты доменов направлены беспорядочно и взаимно компенсируют друг друга. Поэтому ферромагнетик в обычном своем состоянии не имеет результирующего магнитного момента, т. е. его намагниченность равна нулю.