2. Источники магнитного поля

Любой проводник или контур с электрическим током, так же как и движущийся электрический заряд, создают свое собственное магнитное поле. Количественную оценку такого магнитного поля производят с помощью напряженности Н (рис. 5, а), которая определяется законом Био-Савара-Лапласа [4]: элемент контура , по которому течет ток силойI, создает в произвольно выбранной точке А пространства магнитное поле напряженностью

, (11)

где r – расстояние от элемента контура до рассматриваемой точки;

α – угол между r и Δl.

Вектор напряженности магнитного поля , созданный токомI, перпендикулярен плоскости, в которой лежат элемент Δl и отрезок r.

Рассмотрим частные, но важные для практики случаи.

2.1. Магнитное поле прямолинейного проводника с током Суммируя все от всех, на основе уравнения (11) получаем:

. (12)

Согласно рис. 5, б имеем: и. Тогда. Переходя к интегрированию, получаем:.

Таким образом, напряженность поля Н в любой точке, расположенной на расстоянии r от оси прямолинейного проводника, определяют по формуле, А/м:

. (13)

Силовые линии магнитного поля – это концентрические окружности с центрами на оси проводника (рис. 6, а). Направление поля связано с направлением тока правилом правозаходного винта. По мере приближения к оси проводника () поле усиливается, а с удалением – падает, что показано на рис. 6, а сгущением или, соответственно, разряжением силовых линий.

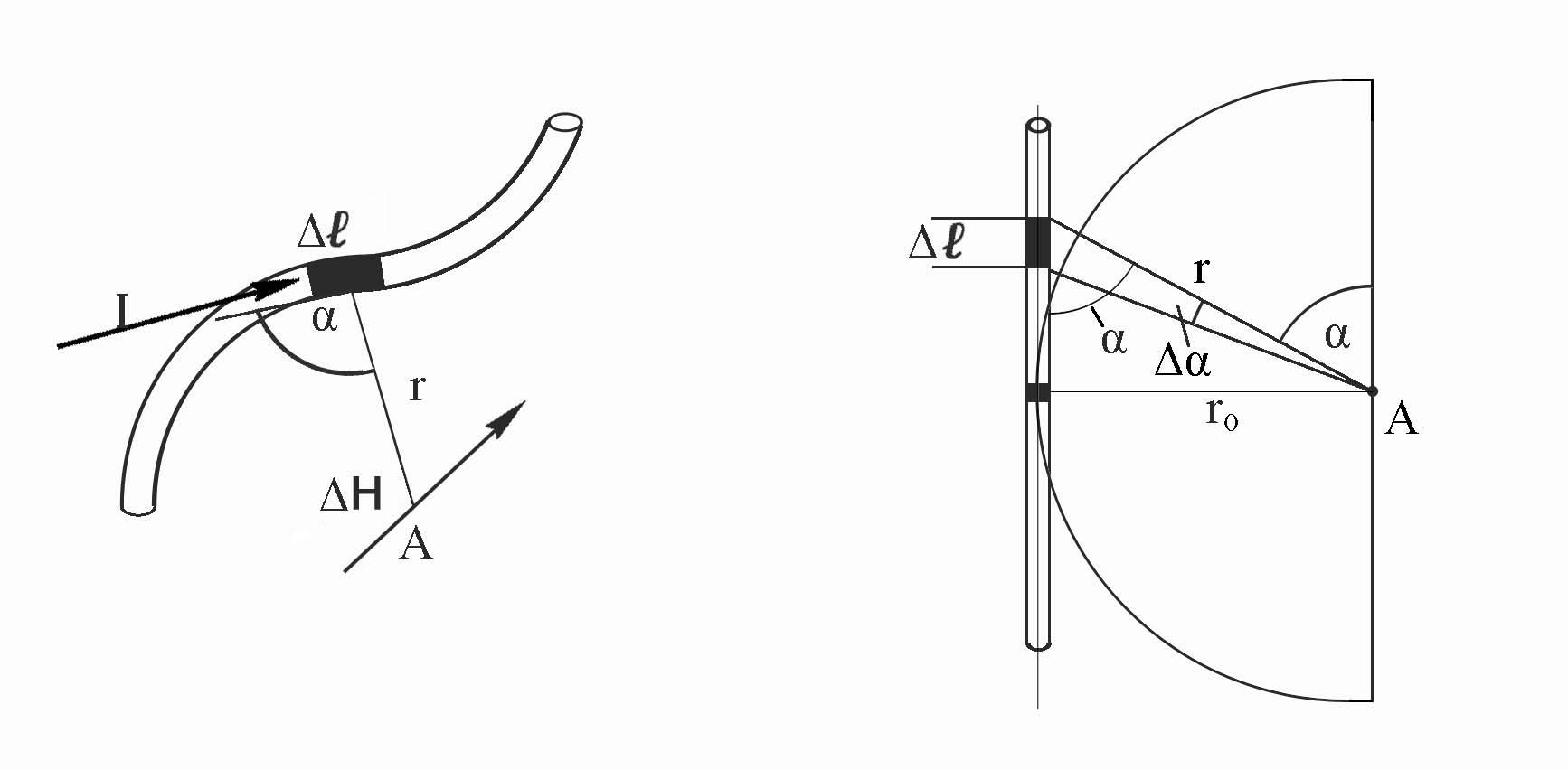
а б

Рис. 5. Иллюстрации к выводу закона Био-Савара-Лапласа

для элемента с током: а – в произвольном контуре;

б – в прямолинейном проводнике

Подчеркнем, что гиперболический закон (13) уменьшения Н верен только для точек вне проводника. Внутри проводника диаметром 2r₀ поле по мере удаления от его геометрической оси линейно возрастает с увеличением r по закону:

. (14)

Таким образом, напряженность поля внутри проводника в пределах r < r₀ (участок 1) линейно зависит от r, т. е. , а вне – приr > r₀ (участок 2) – (рис. 6, б). Напряженность в любой точке, расположенной на поверхности проводника (r = r₀), достигает максимального значения .

Прямолинейные проводники с током в виде медных стержней или гибких кабелей различного сечения применяют для циркулярного намагничивания контролируемых деталей.

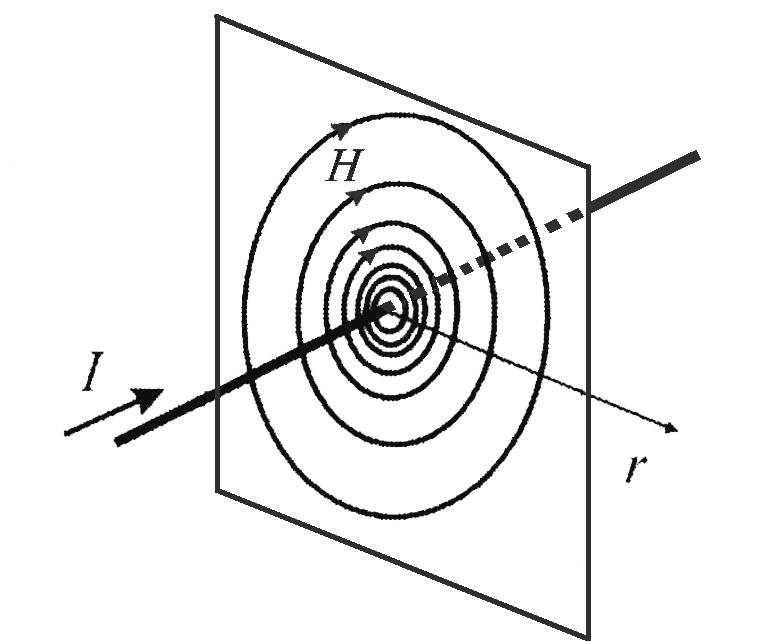
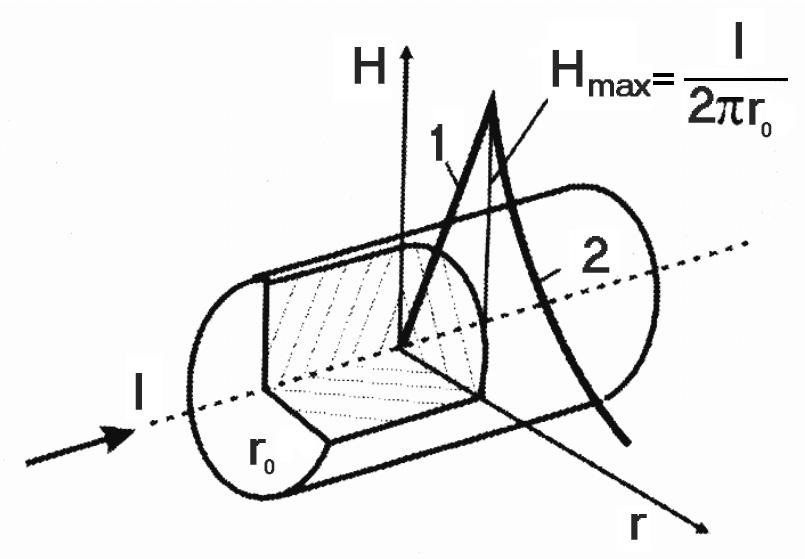
а б

Рис. 6. Магнитное поле прямолинейного проводника с током:

а – линии магнитного поля; б – напряженность поля внутри и

вне проводника

2.2. Магнитное поле кругового тока

В центре кругового тока (рис. 7, а), когда ,и, напряженность

, т. е.. (15)

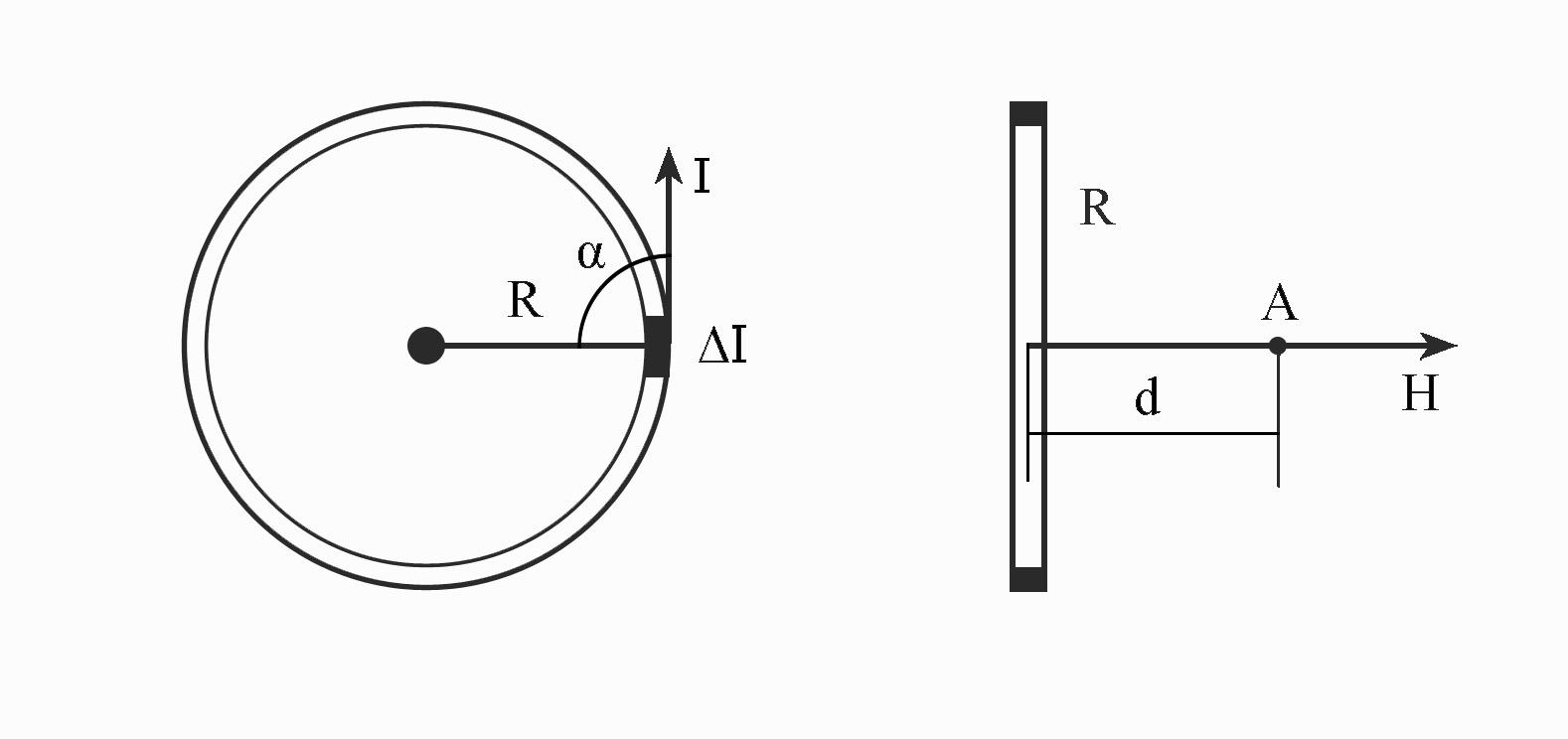
а б

Рис. 7. Магнитное поле кругового тока:

а – в центре; б – на расстоянии dот плоскости его протекания

2.3. Магнитное поле на оси кругового тока

магнитное поле на оси кругового тока на расстоянии d от плоскости его протекания (рис. 7, б) можно рассчитать по формуле:

. (16)

При d= 0 формула (16) переходит в выражение (15). С увеличениемdзначение напряженности поля по оси уменьшается. Если имеетсяwпроводников, уложенных в достаточно тонкую катушку (d0), то в уравнение (16) вместоIвойдет произведениеwI. Длинная катушка называется соленоидом.