
1151
.pdfМИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РФ ДЕПАРТАМЕНТ КАДРОВ И УЧЕБНЫХ ЗАВЕДЕНИЙ
САМАРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ПУТЕЙ СООБЩЕНИЯ
Кафедра "Строительные конструкции и материалы"
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ И РАМЫ. РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
Методические указания по выполнению расчетно-графической работы
для студентов дневной формы обучения
Составители: Е.А.Жичкин Е.С. Жичкина
Самара 2003
УДК 620.10
Сопротивление материалов. Статически определимые балки и рамы. Расчеты на прочность и жесткость. Методические указания по выполнению расчетно-графической работы для студентов дневной формы обучения. - Самара: СамГАПС, 2003. – 24 с.
Утверждено на заседании кафедры. Протокол № 3 от 13 марта 2003 г.
Печатается по решению редакционно-издательского совета академии.
Методические указания по выполнению расчетно-графической работы составлены в соответствии с программой курса "Сопротивление материалов" для студентов специальностей С, МТ, Л, ЭТ и В дневной формы обучения.
Составители: Евгений Александрович Жичкин, к.т.н., доцент Елена Сергеевна Жичкина, к.т.н., доцент
Рецензенты: Сеськин И.Е., профессор СамГАПС, канд. техн. наук, Любимов В.В., доцент кафедры "Теоретическая механика" СГАУ,
канд. физ.-мат. наук
Редактор И.А.Шимина
Компьютерная верстка: А.В.Эрлих
Подписано в печать 19.03.2003 Формат 60х84 1/16 Бумага писчая. Печать оперативная. Усл. п. л. 1,5 Тираж 250 экз. Заказ № 32
© Самарская государственная академия путей сообщения, 2003
2
|
Содержание |
|
1. |
ОСНОВЫ ТЕОРИИ................................................................................................................................. |
4 |
2. |
РАСЧЕТ БАЛКИ....................................................................................................................................... |
8 |
2.1. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР ................................................................................................ |
8 |
|
2.2. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ ОТ ЗАДАННЫХ НАГРУЗОК ............... |
9 |
|
2.3. РАСЧЕТ НЕОБХОДИМОГО ПО ПРОЧНОСТИ ДВУТАВРА............................................................ |
11 |
|
2.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ.............................................................................................. |
12 |
|
2.5. ПОДБОР КВАДРАТНОГО, ПРЯМОУГОЛЬНОГО, КРУГЛОГО И КОЛЬЦЕВОГО СЕЧЕНИЙ .............. |
15 |
|
3. |
РАСЧЕТ РАМЫ ...................................................................................................................................... |
16 |
3.1. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР .............................................................................................. |
17 |
|
3.2. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ ОТ ЗАДАННЫХ НАГРУЗОК ............. |
17 |
|
3.3. РАСЧЕТ НЕОБХОДИМОГО ПО ПРОЧНОСТИ ДВУТАВРА.............................................................. |
19 |
|
3.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ.............................................................................................. |
20 |
|
БИБЛИОГАФИЧЕСКИЙ СПИСОК ................................................................................... |
23 |
|
3

1. ОСНОВЫ ТЕОРИИ
При изгибе в поперечных сечениях бруса возникают изгибающие моменты М и поперечные силы Q (рис. 1). Эти силовые факторы вычисляют при помощи метода сечений. При этом изгибающий момент М считается положительным, когда на левом торце правой отсеченной части бруса он направлен по часовой стрелке, а на правом торце левой отсеченной части — против часовой стрелки. Поперечная сила Q положительна, когда на левом торце правой отсеченной части бруса она направлена вверх, а на правом торце левой отсеченной части — вниз (рис. 1).
Рис. 1. Внутренние силовые факторы, возникающие
впоперечном сечении бруса при изгибе
Впроизвольном сечении бруса, имеющем координату z, поперечная сила Q и изгибающий момент М являются функциями координаты z, т. е. Q = Q(z) и M = M(z). В конкретных задачах сопротивления материалов функции Q(z) и M(z) рассчитывают по следующим правилам [2].
Изгибающий момент М, действующий в поперечном сечении бруса, по величине и знаку равен сумме моментов относительно центральной оси этого сечения всех внешних сил, приложенных к левой части бруса, или сумме моментов (относительно той же оси), взятой с обратным знаком, всех внешних сил, приложенных к правой части:
М М М ; |
(1) |
лев прав |
|
при этом моменты внешних сил должны быть приняты положительными, когда они действуют по часовой стрелке.
Поперечная сила Q по величине и знаку равна сумме проекций всех внешних сил, приложенных к левой части бруса, на нормаль к его продольной оси, проведенной в рассматриваемом поперечном сечении, или сумме проекций (на ту же нормаль), взятой с обратным знаком, всех внешних сил, приложенных к правой части бруса:
4
Q Y Y ; |
(2) |
лев прав |
|
при этом проекции внешних сил на нормаль должны быть приняты положительными, когда они направлены снизу вверх.
Продольная сила N по величине и знаку равна сумме проекций всех внешних сил, приложенных к левой части бруса, на его продольную ось, или сумме проекций (на ту же ось), взятой с обратным знаком, всех внешних сил, приложенных к правой части бруса:
N Z Z ; |
(3) |
лев прав |
|
при этом проекции внешних сил на ось бруса приняты положительными, когда они направлены справа налево.
Графики зависимостей Q = Q(z) и M = M(z), называемые эпюрами поперечных сил и изгибающих моментов, строятся для выявления наиболее опасных сечений, в которых сила Q и/или момент М имеют наибольшие абсолютные значения. При построении эпюр моментов традиционно инженеры-машиностроители и инженеры-транспортники откладывают положительные значения моментов вверх от оси бруса, в этом случае ординаты эпюры моментов располагаются со стороны сжатого волокна. Инженерыстроители откладывают положительные значения моментов вниз от оси бруса, в этом случае ординаты эпюры моментов располагаются со стороны растянутого волокна.
При изгибе в поперечных сечениях возникают нормальные напряжения , которые распределяются по сечению неравномерно. Например, при изгибе бруса двутаврового поперечного сечения эпюра напряжений будет иметь вид, показанный на рис.2.
В случае, когда изгибающий момент М действует в плоскости симметрии сечения (или когда плоскость момента проходит через главную ось сечения), максимальное по абсолютной величине напряжение рассчитывается по формуле
|
|
|
|
M |
|
|
, |
(4) |
|
|
max Wи
где max — максимальное напряжение в сечении в Па, Wи — момент сопротивления изгибу в м3.
y |
М |
|
|
|
|
|
х |
z |
|
 max
max
Рис.2. Распределение нормальных напряжений в сечении двутавра
5

Момент сопротивления изгибу Wи — это геометрическая характеристика сечения. Для стандартных прокатных профилей геометрические характеристики даются в специальных таблицах, которые можно найти в приложениях к учебникам по сопротивлению материалов [1,2].
Для сечений простой формы моменты сопротивления изгибу вычисляются по формулам:
|
|
D3 |
|
|
|
d 4 |
|
|
3 |
|
|
|
d 4 |
|
|
||
для трубы |
Wu |
|
|
1 |
|
|
|
|
0,1D |
|
1 |
|
|
|
|
, |
|
|
|
4 |
|
|
4 |
||||||||||||
32 |
|
D |
|
|
|
D |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где d и D — внутренний и наружный диаметры трубы соответственно;
для прямоугольного сечения |
W |
|
|
bh2 |
, |
x |
|
||||
|
|
6 |
|
||
|
|
|
|
||
где Wx — момент сопротивления изгибу относительно оси х,
b — размер прямоугольного сечения, параллельный оси х,
h — размер прямоугольного сечения, перпендикулярный оси х.
Подбор размеров поперечного сечения осуществляется из условия прочности.
|
max |
|
|
|
M |
|
max |
, или |
|
max |
|
|
|
M |
|
max |
R , |
(5) |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Wx |
|
|
|
|
|
Wx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где — допускаемое напряжение; |
|
|
|
|
|
|
|
|
|
|
||||||||
R — расчетное сопротивление.
Перемещения, возникающие в стержневой системе, вычисляются при помощи
интеграла Мора: |
|
|
|
|
|
|
||
|
|
|
M ( z ) |
|
1 ( z ) |
|
||
|
|
А |
M |
dz , |
||||
|
|
|
EJ |
|
||||
|
|
l |
|
|
||||
|
|
|
|
|
|
|
|
|
где A — перемещение сечения А в заданном направлении, |
||||||||
M z — изгибающий момент от заданной нагрузки, |
||||||||
|
|
1 z — изгибающий |
момент от единичного фиктивного силового фактора, |
|||||
M |
||||||||
приложенного в сечении А в направлении искомого перемещения, E — модуль Юнга,
J — момент инерции сечения относительно оси, перпендикулярной к плоскости действия изгибающего момента.
Если на некотором участке функция M 1 z — линейная функция z и жесткость EJ постоянна, то интеграл Мора может быть вычислен методом Верещагина по формуле
l |
M ( z ) |
|
1 ( z ) |
|
|
|
|
|
|
|
||
M |
|
1 |
|
|
|
|
|
|||||
|
dz |
M M 1C |
, |
(6) |
||||||||
EJ |
|
EJ |
||||||||||
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
где М — площадь эпюры нагрузочных моментов M ,
M 1C — ордината эпюры моментов M 1 , находящаяся под центром тяжести C
эпюры нагрузочных моментов M .
Для простейших эпюр моментов значения площадей M и координат центров тяжести zC даны в таблице 1.
Если эпюра не является простейшей, то ее следует расщепить, т.е. представить в виде совокупности простейших эпюр.
6
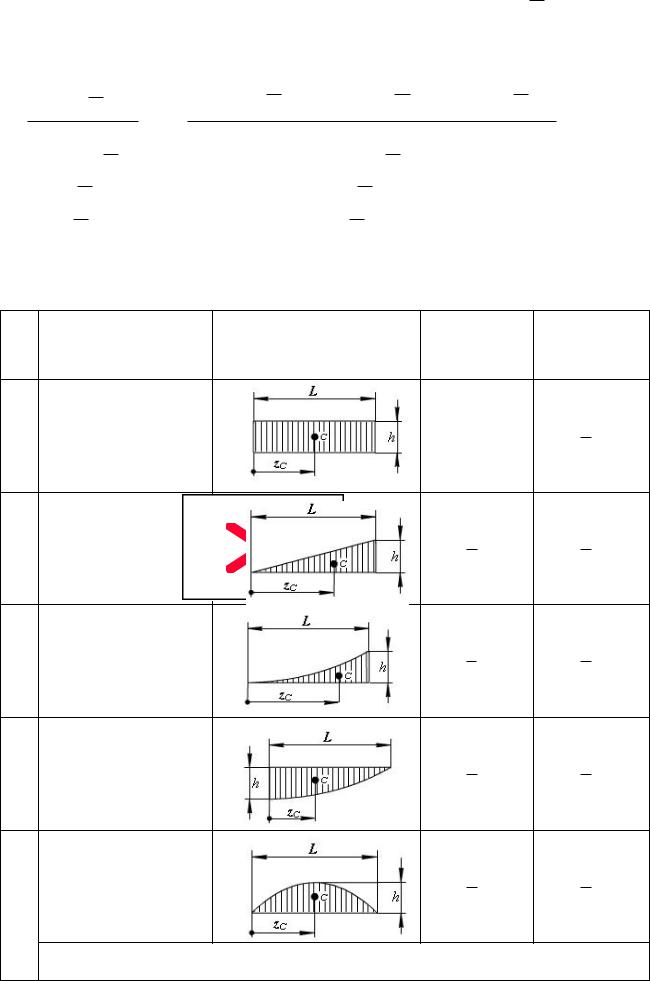
Интеграл Мора можно вычислить и по формуле Симпсона. Применение формулы |
||||||||||||
Симпсона для определения перемещений дает точные результаты, если в интеграле Мора |
||||||||||||
функция M z является линейной или квадратичной функцией z, а M 1 z |
— линейной |
|||||||||||
функцией и жесткость EJ постоянна. |
|
|
|
|
|
|
||||||
Формула Симпсона для вычисления интеграла Мора на некотором участке имеет |
||||||||||||
вид: |
|
|
|
|
l M нач M 1нач 4M сред |
M 1сред M кон M 1кон |
|
|
||||
l |
M ( z ) M |
1 |
( z ) |
|
|
|
||||||
|
|
|
dz |
|
|
|
|
, |
|
(7) |
||
EJ |
|
|
6 EJ |
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
где M нач , M 1нач — величины моментов M и M 1 в начале участка, |
|
|
||||||||||
M сред , M 1сред — величины моментов M и M 1 |
в середине участка, |
|
|
|||||||||
M кон , M 1кон — величины моментов M и M 1 в конце участка. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
Площади и координаты центров тяжести эпюр |
|
|
|
|||||
№ |
Тип эпюры |
Эпюра |
Площадь |
Координата |
||||||||
эпюры |
ц.т. эпюры |
|||||||||||
|
|
|
|
|
|
|||||||
1 |
прямоугольник |
|
L h |
zC |
1 L |
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
прямоугольный |
|
|
1 |
L h |
zC |
2 |
L |
||||
треугольник |
|
2 |
3 |
|||||||||
|
|
|
|
|
|
|||||||
3 |
криволинейный |
|
|
1 |
L h |
zC |
3 |
L |
||||
треугольник |
|
3 |
4 |
|||||||||
|
|
|
|
|
|
|||||||
4 |
половина |
|
|
|
2 |
L h |
zC |
3 |
L |
|||
"горбушки" |
|
3 |
8 |
|||||||||
|
|
|
|
|
|
|||||||
5 |
"горбушка" |
|
|
|
2 L h |
zC |
1 L |
|||||
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
Высота h "горбушки" вычисляется по формуле h=qL2/8 |
|
|
|||||||
7

Метод Верещагина и формула Симпсона дают один и тот же результат. В случае, если эпюры простые, предпочтительней применение метода Верещагина. Если же приходится расщеплять эпюру, то лучше применять интеграл Симпсона.
2. РАСЧЕТ БАЛКИ
Для балки, показанной на рис.3, требуется:
1)определить реакции опор и сделать проверку;
2)построить эпюры внутренних силовых факторов;
3)из расчета на прочность по максимальным нормальным напряжениям подобрать
номер двутаврового профиля, из которого следует изготовить балку, приняв допускаемое напряжение 200 МПа (или расчетное сопротивление R 200 МПа );
4)с помощью интегралов Мора найти вертикальное перемещение сечения К1 и
угол поворота сечения К2, приняв модуль упругости Е 200ГПа ;
5) из расчета на прочность подобрать для балки круговое, кольцевое, квадратное и прямоугольное сечения и сравнить массы всех рассчитанных балок, включая двутавровую; принять соотношение размеров прямоугольника h b 1,5 и кольца
b 1,5 и кольца
D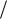 d 1,5 .
d 1,5 .
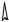 y 40кН/м
y 40кН/м
160кНм |
40кН |
A |
|
|
B |
K2 |
K1 |
|
|
||
2м |
2м |
|
2м |
Рис.3. Исходная расчетная схема
2.1. Определение реакций опор
Найдем реакции RA и RВ (рис.4b) из уравнений равновесия балки.
M A |
0; |
RB 4 40 2 3 160 40 6 0 RB 80 кН . |
M B |
0; |
RA 4 40 2 1 160 40 2 0 RA 40 кН . |
Изобразим найденные реакции опор на схеме (рис.4c). Поскольку RA и RB имеют положительные значения, то направление реакций остается прежним. Записываем 40 кН вместо RA и 80 кН вместо RB.
Сделаем проверку по рис.4с:
Fy 0; |
40 40 2 80 40 0 |
|
120 120 0 |
|
0 0 . |
Полученное тождество показывает, что реакции опор найдены правильно.
8

 y 40кН/м
y 40кН/м
160кНм |
40кН |
A |
|
|
B |
K2 |
a) |
K1 |
|
|
|||
|
|
|
|||
2м |
2м |
|
2м |
|
40кН/м |
|
|
|
RA |
RB |
40кН |
|
160кНм |
|||
|
A |
|
|
B |
K2 |
b) |
K1 |
|
|
|||
2м |
2м |
|
2м |
|
|
40кН/м |
|
|
40кН |
160кНм |
80кН |
40кН |
A |
|
|
B |
K2 |
|
K1 |
|
|
c) |
||
|
|
|
|
||
2м |
2м |
|
2м |
|
Рис.4. К определению реакций опор
2.2. Построение эпюр внутренних силовых факторов от заданных нагрузок
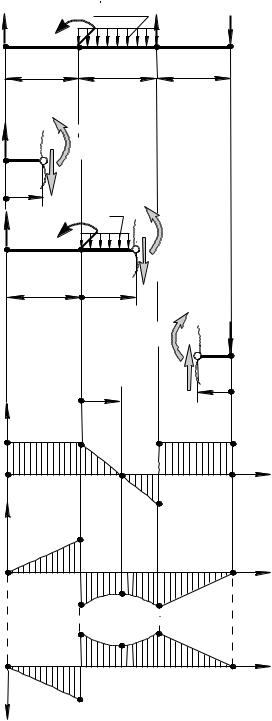
Строим эпюры поперечной силы Q и изгибающего момента M, используя метод сечений. Разделим балку на участки: 1-й участок — А-К1, 2-й участок — К1-В, 3-й участок В-К2 (рис.5а).
Участок А-К1
Уравнения равновесия левой отсеченной части (рис.5b).
Fy 0; |
40 Q 0 ; |
|
Q 40 кН . |
|
M s 0; 40 z1 M 0 ; |
|
|
M 40 z1 ; 0 z1 2м . |
|
Найдем значения момента в начале и конце участка. |
|
|||
В сечении А при z1 0 |
M 0 , т.е. |
M A 0 . |
|
|
В сечении К1 при z1 2м M 40 2 80 , т.е. |
M K1 80 кН м . |
|||
По найденным значениям строим на участке А-К1 эпюры Q (рис.5е) и M (рис.5f и 5g). На рис.5f эпюра изгибающих моментов построена на сжатом волокне, так строят эпюры инженеры - транспортники и машиностроители. На рис.5g эпюра моментов построена на растянутом волокне, так делают инженеры - строители.
9
40кН |
160кНм |
40кН/м |
80кН |
40кН |
|
||||
|
|
|
|
|
|
||||
A |
|
|
|
|
|
B |
|
K2 |
|
|
|
K1 |
|
|
|
|
a) |
||
|
|
2м |
2м |
|
|
2м |
|
||
|
|
|
|
|
|
||||
|
40 |
M |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
b) |
||
|
s |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z1 |
Q |
|
|
|
|
|
|
|
40 |
|
|
|
40 |
|
|
|
|
|
|
160 |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
|
|
|
|
|
c) |
|
|
|
K1 |
s |
|
|
|
|
||
|
|
|
|
Q |
|
|
|
||
|
|
2м |
z2 |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
M |
|
40 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
s |
K2 |
d) |
|
|
|
|
|
|
Q |
|
|
|
|
|
|
1м |
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
[кН] 40 |
|
40 |
|
40 |
|
40 |
|
||
|
|
|
|
|
|
||||
|
|
|
|
С |
|
|
|
z |
e) |
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
-40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[кНм] |
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
f) |
|
|
|
|
|
|
|
|
|
|
|
|
-80 |
|
-60 |
|
-80 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
-80 |
|
-60 |
|
-80 |
|
|
|
|
|
|
|
|
|
|
|
z |
g) |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[кНм] |
|
|
80 |
|
|
|
|
|
|
Рис.5. К построению эпюр внутренних силовых факторов |
|||||||||
Участок К1-В Составим уравнения равновесия левой отсеченной части (рис.5с):
Fy 0; 40 40 z2 Q 0 ;
Q40 40 z2 ;
M s 0; 40 2 z2 160 40 z2 0.5z2 M 0 ;
M 40 2 z |
2 |
160 20 z 2 |
; |
где 0 z |
2 |
2м . |
|
2 |
|
|
|
||
|
|
10 |
|
|
|
|
