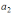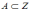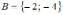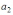ЗАДАНИЕ
N 1
Тема:
Правила дифференцирования
Производная
функции
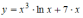 равна …
равна …
Решение:
Для
нахождения производной необходимо
воспользоваться правилами
 ,
,
 ,
,
 ,
где c
– постоянная величина, а U
и
V
– некоторые функции, зависящие от x,
и формулами
,
где c
– постоянная величина, а U
и
V
– некоторые функции, зависящие от x,
и формулами
 Тогда
получим
Тогда
получим

|
ЗАДАНИЕ
N 2
Тема:
Производная функции в точке
Если
|
Решение:
Напоминаем,
что производная суммы двух функций
равна сумме производных этих функций.
Тогда имеем
 Пусть
Пусть
 .
Получим
.
Получим

ЗАДАНИЕ
N 3
Тема:
Дифференциал функции
Для
приближенного вычисления значения
функции y(x)
в точке
 можно
использовать формулу
можно
использовать формулу
 где
где
 приращение
функции в точке
приращение
функции в точке
 Функция
y(x)
определяется из условия задачи.
Значения
Функция
y(x)
определяется из условия задачи.
Значения
 и
и
 выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить
 и
при этом
и
при этом
 ,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
 равно …
равно …
Решение:
 .
Так как
.
Так как
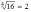 ,
то можно рассмотреть функцию
,
то можно рассмотреть функцию
 Пусть
Пусть
 тогда
тогда
 Имеем:
Имеем:

 По
формуле
По
формуле
 получим:
получим:

ЗАДАНИЕ
N 4
Тема:
Наибольшее и наименьшее значения
функции
Функция
 имеет
на отрезке
имеет
на отрезке
 наибольшее
значение, равное …
наибольшее
значение, равное …
Решение:
Заметим,
что функция
 непрерывна
на отрезке
непрерывна
на отрезке
 .
Найдем
производную
.
Найдем
производную
 В
данном задании критическими являются
точки, в которых производная равна
нулю. То есть
В
данном задании критическими являются
точки, в которых производная равна
нулю. То есть
 .
Корнями полученного уравнения являются
.
Корнями полученного уравнения являются
 и
и
 Обращаем
внимание на то, что точка
Обращаем
внимание на то, что точка
 не
принадлежит отрезку
не
принадлежит отрезку
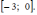 Вычислим
значения функции в точке
Вычислим
значения функции в точке
 и
на концах данного отрезка.
и
на концах данного отрезка.
 Наибольшее
значение функции на указанном промежутке
равно 10.
Наибольшее
значение функции на указанном промежутке
равно 10.
ЗАДАНИЕ
N 6
Тема:
Экстремум функции
Для
функции
 точка
минимума
точка
минимума
 равна …
равна …
Решение:
Заметим,
что
 .
Для отыскания точек экстремума нужно
найти точки, в которых производная
равна нулю или не существует.
.
Для отыскания точек экстремума нужно
найти точки, в которых производная
равна нулю или не существует.
 Из
полученного уравнения имеем
Из
полученного уравнения имеем
 Отметим
эти точки на числовой прямой. Напоминаем,
что в точке
Отметим
эти точки на числовой прямой. Напоминаем,
что в точке
 функция
не существует.
Найдем знак производной
функция
не существует.
Найдем знак производной
 на
каждом из получившихся промежутков.
на
каждом из получившихся промежутков.
 Точки
Точки
 и
и
 являются
экстремальными, так как при переходе
через эти точки производная меняет
знак.
являются
экстремальными, так как при переходе
через эти точки производная меняет
знак.
 –
точка минимума, так как производная
меняет знак с «-» на «+».
–
точка минимума, так как производная
меняет знак с «-» на «+».
ЗАДАНИЕ
N 7
Тема:
Действия над множествами
Пусть
на рисунке изображены множества
 и
и

 Тогда
заштрихованная область соответствует
множеству …
Тогда
заштрихованная область соответствует
множеству …
ЗАДАНИЕ
N 8
Тема:
Прямое произведение двух множеств
Пусть
 ,
,
 .
Тогда прямое произведение
.
Тогда прямое произведение
 равно …
равно …
Решение:
Прямое
произведение
 содержит
множество упорядоченных пар вида
содержит
множество упорядоченных пар вида
 ,
в которых x
пробегает все значения из множества
A,
а y –
все значения из множества B,
тогда
,
в которых x
пробегает все значения из множества
A,
а y –
все значения из множества B,
тогда
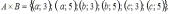
ЗАДАНИЕ
N 9
Тема:
Основные понятия теории множеств
Даны
множества
 нечетное
нечетное и
и
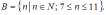 Тогда
верными будут утверждения …
Тогда
верными будут утверждения …
|
|
|
множество A бесконечно |
|
|
|
|
Решение:
Обращаем
внимание, что множества заданы с помощью
характеристического свойства. Зададим
их перечислением элементов. Получим
 и
и
 .
Тогда очевидно, что утверждения
.
Тогда очевидно, что утверждения
 и
«множество A
бесконечно» являются верными, а
утверждения
и
«множество A
бесконечно» являются верными, а
утверждения
 и
и
 являются
ложными.
являются
ложными.
ЗАДАНИЕ
N 10
Тема:
Числовые множества
Числовые
множества – это множества, элементами
которых являются числа.
Примеры таких
множеств:
R – множество действительных
чисел,
Q – множество рациональных
чисел,
Z – множество целых чисел,
N
– множество натуральных чисел.
Пусть
дано множество
 ,
тогда верными будут утверждения …
,
тогда верными будут утверждения …
|
|
|
|
|
|
|
|
Решение:
Элементами
множества A
являются целые числа. Значит, справедливы
утверждения, что
 и
и
 .
Так как отрицательные числа не являются
натуральными, то
.
Так как отрицательные числа не являются
натуральными, то
 неверно.
Неверным является и
неверно.
Неверным является и
 ,
так как множество A
содержит в себе всего три числа.
,
так как множество A
содержит в себе всего три числа.
ЗАДАНИЕ
N 11
Тема:
Способы задания множеств, конечные и
бесконечные множества
Даны
множества
 и
и
 Тогда
верными будут утверждения …
Тогда
верными будут утверждения …
|
|
|
|
|
|
|
|
Решение:
Обращаем
внимание, что множества заданы с помощью
характеристического свойства. Зададим
их перечислением элементов. Элементы
множества A
являются корнями уравнения
 .
Решим его, получим
.
Решим его, получим
 .
Значит,
.
Значит,
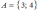 и
утверждение
и
утверждение
 ложное.
Аналогично получим
ложное.
Аналогично получим
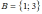 .
Для множеств A и B элемент 3 является
общим, значит, утверждение
.
Для множеств A и B элемент 3 является
общим, значит, утверждение
 истинное.
По этой же причине утверждение
истинное.
По этой же причине утверждение
 ложное.
Объединение множеств содержит все
элементы, которые содержатся в каждом
из них, поэтому утверждение
ложное.
Объединение множеств содержит все
элементы, которые содержатся в каждом
из них, поэтому утверждение
 истинное.
истинное.
ЗАДАНИЕ
N 12
Тема:
Действия над конечными множествами
Даны
множества
 и
и
 .
Тогда
.
Тогда
 равно …
равно …
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 13
Тема:
Первый замечательный предел
 равен …
равен …
Решение:
Напоминаем,
что для вычисления предела функции
нужно воспользоваться первым замечательным
пределом
 и
соотношением
и
соотношением
 .
Для
этого необходимо выполнить замену
переменной
.
Для
этого необходимо выполнить замену
переменной
 откуда
откуда
 Учитывая,
что
Учитывая,
что
 при
при
 ,
получаем
,
получаем
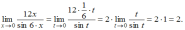
ЗАДАНИЕ
N 14
Тема:
Предел функции в точке
Предел
функции
 равен …
равен …
Решение:
Напоминаем,
что для вычисления предела многочлена
при
 достаточно
вместо переменной
достаточно
вместо переменной
 поставить
значение
поставить
значение
 ,
к которому она стремится, и выполнить
соответствующие действия:
,
к которому она стремится, и выполнить
соответствующие действия:
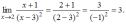
ЗАДАНИЕ
N 15
Тема:
Способы задания числовых
последовательностей
Дана
числовая последовательность
 Установите
соответствие между номером и
соответствующим членом данной
последовательности.
Установите
соответствие между номером и
соответствующим членом данной
последовательности.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
того чтобы найти определенный член
последовательности, нужно вместо
 в
данное равенство подставить его номер.
в
данное равенство подставить его номер.


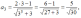

Задание n 16 Тема: Второй замечательный предел
ЗАДАНИЕ
N 17
Тема:
Раскрытие неопределенности вида "ноль
на ноль"
 равен …
равен …
Решение:
Обращаем
внимание, что предел данной функции
нельзя вычислить непосредственной
подстановкой предельного значения
аргумента в выражение, так как при этом
получается неопределенность вида
 .
Поэтому нужно преобразовать функцию,
используя формулу разности квадратов
.
Поэтому нужно преобразовать функцию,
используя формулу разности квадратов
 .
Имеем:
.
Имеем:
 Сократив
полученную дробь на критический
множитель
Сократив
полученную дробь на критический
множитель
 ,
и подставив предельное значение
аргумента в оставшееся выражение,
получим
,
и подставив предельное значение
аргумента в оставшееся выражение,
получим

ЗАДАНИЕ
N 18
Тема:
Раскрытие неопределенности вида
"бесконечность на бесконечность"
 равен …
равен …
Решение:
Обращаем
внимание, что так как
 и
и
 то
в данном случае имеет место неопределенность
вида
то
в данном случае имеет место неопределенность
вида
 .
Для ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на
.
Для ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на
 (наивысшую
степень
(наивысшую
степень
 в
данной дроби). Тогда, зная, что
в
данной дроби). Тогда, зная, что
 ,
получим:
,
получим:

ЗАДАНИЕ
N 19
Тема:
Методы вычисления неопределенных
интегралов
Неопределенный
интеграл
 равен …
равен …
Решение:
Обращаем
внимание, что подстановка
 приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному:
 Для
этого нужно найти дифференциал от обеих
частей подстановки:
Для
этого нужно найти дифференциал от обеих
частей подстановки:
 .
Подставляя получившиеся выражения в
исходный интеграл, получаем
.
Подставляя получившиеся выражения в
исходный интеграл, получаем
 Заменив
Заменив
 его
выражением из подстановки, имеем
его
выражением из подстановки, имеем

ЗАДАНИЕ
N 20
Тема:
Неопределенный интеграл
Неопределенный
интеграл
 равен …
равен …
ЗАДАНИЕ
N 21
Тема:
Геометрические приложения определенного
интеграла
 Площадь
фигуры, изображенной на заданном
рисунке, равна …
Площадь
фигуры, изображенной на заданном
рисунке, равна …
Решение:
Обращаем
внимание, что площадь данной плоской
фигуры вычисляется по формуле
 Тогда
Тогда
 Получаем,
что площадь фигуры равна
Получаем,
что площадь фигуры равна
 (кв.
ед.).
(кв.
ед.).
ЗАДАНИЕ
N 22
Тема:
Свойства определенного интеграла
Определенный
интеграл
 равен …
равен …
Решение:
Обращаем
внимание, что используя свойства
интеграла
 и
и
 ,
исходный интеграл можно представить
в виде разности двух выражений и,
применяя формулу Ньютона – Лейбница
,
исходный интеграл можно представить
в виде разности двух выражений и,
применяя формулу Ньютона – Лейбница
 ,
получим:
,
получим:

ЗАДАНИЕ
N 23
Тема:
Определенный интеграл. Формула Ньютона
- Лейбница
Определенный
интеграл
 равен …
равен …
Решение:
Напоминаем,
что формула Ньютона – Лейбница имеет
вид
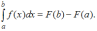 В
нашем случае, используя формулу
В
нашем случае, используя формулу
 ,
имеем
,
имеем

ЗАДАНИЕ
N 24
Тема:
Физические приложения определенного
интеграла
Скорость
движения тела задана уравнением
 .
Тогда путь, пройденный телом за время
от второй секунды до четвертой секунды
движения, равен …
.
Тогда путь, пройденный телом за время
от второй секунды до четвертой секунды
движения, равен …
Решение:
Напоминаем,
что путь
 ,
пройденный телом за отрезок времени
от
,
пройденный телом за отрезок времени
от
 до
до
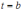 ,
движущимся прямолинейно со скоростью
,
движущимся прямолинейно со скоростью
 ,
вычисляется по формуле:
,
вычисляется по формуле:
 .
Тогда,
используя условие, имеем:
.
Тогда,
используя условие, имеем:

ЗАДАНИЕ N 25 Тема: Элементы комбинаторики Автомобилю может быть присвоен номер, состоящий из 4 цифр: 1, 3, 5, 7. Цифры в номере повторяться не могут. Тогда максимальное количество автомобилей, которым могут быть присвоены такие номера, равно …
Решение:
Число
различных номеров из 4 цифр: 1, 3, 5, 7, в
которых каждая цифра встречается ровно
один раз, равно числу перестановок из
четырех элементов:

ЗАДАНИЕ N 26 Тема: Классическое определение вероятности В урне 10 шаров, имеющих номера: 1, 2, …, 10. Наугад вынутый шар имеет номер, кратный 3, с вероятностью, равной …
Решение:
Вероятностью
Р(А)
события А
называется отношение числа благоприятных
для А
исходов к числу всех равновозможных
исходов.
По условию задачи число
благоприятных исходов, то есть количество
выпадений номеров, кратных 3: 3, 6 и 9,
равно 3. Число всех равновозможных
исходов равно 10, тогда

ЗАДАНИЕ
N 27
Тема:
Объем выборки
Объем
выборки, заданной статистическим
распределением
 ,
равен …
,
равен …
Решение: Случайная величина Х принимает некоторое значение 120 раз, второе значение − 180 раз, третье значение − 205 раз и четвертое значение 95 раз. Тогда 120 + 180 + + 205 + 95 = 600 – объем выборки.
ЗАДАНИЕ
N 28
Тема:
Характеристики вариационного ряда.
Выборочное среднее
Выборочное
среднее для вариационного ряда
 равно …
равно …
ЗАДАНИЕ
N 29
Тема:
Математическое ожидание дискретной
случайной величины
Математическое
ожидание М(Х)
случайной величины, имеющей закон
распределения вероятностей
 ,
равно …
,
равно …
Решение:
Воспользуемся
формулой
 где
где
 –
значение дискретной случайной величины;
а
–
значение дискретной случайной величины;
а
 –
вероятность, с которой дискретная
случайная величина принимает значение
–
вероятность, с которой дискретная
случайная величина принимает значение
 .
Тогда
.
Тогда

ЗАДАНИЕ N 30 Тема: Теоремы сложения и умножения вероятностей В первой урне 2 белых и 3 черных шара, во второй − 4 белых и 6 черных шаров. Из каждой урны вынули по одному шару. Вероятность того, что оба вынутых шара будут белыми, равна …
Решение:
Пусть
событие А
означает, что из первой урны вынули
белый шар, тогда
 Событие
В
означает, что из второй урны вынули
белый шар, значит,
Событие
В
означает, что из второй урны вынули
белый шар, значит,
 События
А
и В
являются независимыми. Тогда вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий:
События
А
и В
являются независимыми. Тогда вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий:

ЗАДАНИЕ N 1 Тема: Классическое определение вероятности В урне 30 красных, 25 зеленых и 75 желтых шаров. Наугад вынутый шар окажется красным с вероятностью, равной …
ЗАДАНИЕ
N 2
Тема:
Объем выборки
Объем
выборки, заданной статистическим
распределением
 ,
равен …
,
равен …
Решение: Случайная величина Х принимает некоторое значение 120 раз, второе значение − 180 раз, третье значение − 205 раз и четвертое значение 95 раз. Тогда 120 + 180 + + 205 + 95 = 600 – объем выборки.
ЗАДАНИЕ N 3 Тема: Элементы комбинаторики Пин–код пластиковой карты состоит из 4 цифр: 4, 5, 6, 7. Если бы каждая цифра встречалась ровно один раз, то максимальное количество карт с такими кодами было бы равно …
Решение:
Число
различных кодов, состоящих из 4 цифр:
4, 5, 6, 7, в которых каждая цифра встречается
ровно один раз, равно числу перестановок
из четырех элементов:

ЗАДАНИЕ
N 4
Тема:
Математическое ожидание дискретной
случайной величины
Математическое
ожидание М(Х)
случайной величины, имеющей закон
распределения вероятностей
 ,
равно …
,
равно …
ЗАДАНИЕ
N 5
Тема:
Характеристики вариационного ряда.
Выборочное среднее
Выборочное
среднее для вариационного ряда
 равно …
равно …
Решение:
Выборочным
средним называется среднее арифметическое
всех значений выборки:
 Обращаем
внимание, что значение «1» некоторая
случайная величина
принимает 2 раза,
значение «4» – 2 раза,
значение «8» – 5 раз и
значение «10»− 1 раз. Тогда
среднее арифметическое всех значений
выборки
равно
Обращаем
внимание, что значение «1» некоторая
случайная величина
принимает 2 раза,
значение «4» – 2 раза,
значение «8» – 5 раз и
значение «10»− 1 раз. Тогда
среднее арифметическое всех значений
выборки
равно

ЗАДАНИЕ
N 6
Тема:
Теоремы сложения и умножения
вероятностей
Первый
спортсмен попадает в мишень с вероятностью
 ,
а второй – с
вероятностью
,
а второй – с
вероятностью
 .
Оба спортсмена стреляют одновременно.
Вероятность того, что они оба промахнутся,
равна …
.
Оба спортсмена стреляют одновременно.
Вероятность того, что они оба промахнутся,
равна …
Решение:
Если
первый спортсмен попадает в мишень с
вероятностью
 ,
то вероятность
промаха равна
,
то вероятность
промаха равна
 .
Аналогично вероятность промаха для
второго спортсмена равна
.
Аналогично вероятность промаха для
второго спортсмена равна
 .
Тогда
вероятность совместного появления
двух независимых событий (два промаха)
равна произведению вероятностей этих
событий:
.
Тогда
вероятность совместного появления
двух независимых событий (два промаха)
равна произведению вероятностей этих
событий:

ЗАДАНИЕ
N 7
Тема:
Правила дифференцирования
Производная
функции
 равна …
равна …
ЗАДАНИЕ
N 8
Тема:
Экстремум функции
Для
функции
 точка
максимума
точка
максимума
 равна …
равна …
Решение:
Заметим,
что
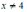 .
Для отыскания точек экстремума нужно
найти точки, в которых производная
равна нулю или не существует.
.
Для отыскания точек экстремума нужно
найти точки, в которых производная
равна нулю или не существует.
 Из
полученного уравнения имеем
Из
полученного уравнения имеем
 Отметим
эти точки на числовой прямой. Напоминаем,
что в точке
Отметим
эти точки на числовой прямой. Напоминаем,
что в точке
 функция
не существует.
Найдем знак производной
функция
не существует.
Найдем знак производной
 на
каждом из получившихся промежутков.
на
каждом из получившихся промежутков.
 Точки
Точки
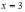 и
и
 являются
экстремальными, так как при переходе
через эти точки производная меняет
знак.
являются
экстремальными, так как при переходе
через эти точки производная меняет
знак.
 –
точка максимума, так как производная
меняет знак с «+» на «-».
–
точка максимума, так как производная
меняет знак с «+» на «-».
ЗАДАНИЕ
N 9
Тема:
Дифференциал функции
Для
приближенного вычисления значения
функции y(x)
в точке
 можно
использовать приближенную формулу
можно
использовать приближенную формулу
 где
где
 приращение
функции в точке
приращение
функции в точке
 Функция
y(x)
определяется из условия задачи.
Значения
Функция
y(x)
определяется из условия задачи.
Значения
 и
и
 выбираются
так, чтобы можно было вычислить
выбираются
так, чтобы можно было вычислить
 и
при этом
и
при этом
 ,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
,
взятое по модулю, было бы как можно
меньше.
Тогда приближенное значение
выражения
 равно …
равно …
Решение:
 .
. Так
как
Так
как
 ,
то можно рассмотреть функцию
,
то можно рассмотреть функцию

 Тогда
Тогда

 По
формуле
По
формуле
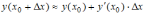 получим
получим

ЗАДАНИЕ
N 11
Тема:
Наибольшее и наименьшее значения
функции
Наименьшее
значение функции
 на
отрезке
на
отрезке  равно …
равно …
Решение:
Заметим,
что функция
 непрерывна
на отрезке
непрерывна
на отрезке  .
Найдем
значения функции на концах отрезка:
.
Найдем
значения функции на концах отрезка:
 Найдем
производную данной функции.
Найдем
производную данной функции.
 Тогда
Тогда
 Так
как
Так
как
 то
нужно найти только
то
нужно найти только

 Сравнивая
значения
Сравнивая
значения
 и
и
 ,
определим, что наименьшее значение
функции равно 1.
,
определим, что наименьшее значение
функции равно 1.
ЗАДАНИЕ
N 12
Тема:
Производная функции в точке
Если
 ,
то
,
то
 принимает
значение, равное …
принимает
значение, равное …
Решение:
Напоминаем,
что производная суммы двух функций
равна сумме производных этих функций.
Тогда имеем
 .
Пусть
.
Пусть
 .
Получим
.
Получим

ЗАДАНИЕ
N 13
Тема:
Действия над конечными множествами
Даны
множества
 и
и
 .
Тогда
.
Тогда
 равно …
равно …
ЗАДАНИЕ
N 14
Тема:
Числовые множества
Числовые
множества – это множества, элементами
которых являются числа.
Примеры таких
множеств:
R
– множество действительных чисел,
Q
– множество рациональных чисел,
Z
– множество целых чисел,
N
– множество натуральных чисел.
Пусть
дано множество
 ,
тогда верными будут утверждения …
,
тогда верными будут утверждения …
|
|
|
|
|
|
|
|
Решение:
Элементами
множества A
являются рациональные числа. Значит,
справедливы утверждения, что
 и
и
 .
Числа
.
Числа
 и
и
 являются
рациональными и не принадлежат множеству
целых и тем более натуральных чисел,
поэтому два оставшихся утверждения
ложные.
являются
рациональными и не принадлежат множеству
целых и тем более натуральных чисел,
поэтому два оставшихся утверждения
ложные.
ЗАДАНИЕ
N 15
Тема:
Прямое произведение двух множеств
Пусть
 ,
,
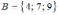 .
Тогда прямое произведение
.
Тогда прямое произведение
 равно …
равно …
Решение:
Прямое
произведение
 содержит
множество упорядоченных пар вида
содержит
множество упорядоченных пар вида
 ,
в которых x
пробегает все значения из множества
A,
а y –
все значения из множества B,
тогда
,
в которых x
пробегает все значения из множества
A,
а y –
все значения из множества B,
тогда

ЗАДАНИЕ
N 16
Тема:
Основные понятия теории множеств
Даны
множества
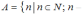 четное
четное и
и
 Тогда
верными будут утверждения …
Тогда
верными будут утверждения …
|
|
|
|
|
|
|
множество A конечно |
Решение:
Обращаем
внимание, что множества заданы с помощью
характеристического свойства. Зададим
их перечислением элементов. Получим
 и
и
 .
Здесь элементы множества B являются
корнями квадратного уравнения
.
Здесь элементы множества B являются
корнями квадратного уравнения
 .
Тогда очевидно, что утверждения
.
Тогда очевидно, что утверждения
 и
и
 являются
верными, а утверждения
являются
верными, а утверждения
 и
«множество A
конечно» являются ложными.
и
«множество A
конечно» являются ложными.
ЗАДАНИЕ
N 17
Тема:
Действия над множествами
Пусть
на рисунке изображены множества
 и
и

 Тогда
заштрихованная область соответствует
множеству …
Тогда
заштрихованная область соответствует
множеству …
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 18
Тема:
Способы задания множеств, конечные и
бесконечные множества
Даны
множества
 и
и
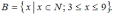 Тогда
верными будут утверждения …
Тогда
верными будут утверждения …
|
|
|
|
|
|
|
|
Решение:
Обращаем
внимание, что множества заданы с помощью
характеристического свойства.
Зададим
эти же множества перечислением
элементов.
Получим
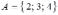 и
и
 .
Очевидно, что утверждение
.
Очевидно, что утверждение
 истинное,
а
истинное,
а
 ложное.
Для множеств A и B элементы 3 и 4 являются
общими. Значит, утверждение
ложное.
Для множеств A и B элементы 3 и 4 являются
общими. Значит, утверждение
 истинное.
По этой же причине утверждение
истинное.
По этой же причине утверждение
 ложное.
ложное.
ЗАДАНИЕ
N 19
Тема:
Определенный интеграл. Формула Ньютона
- Лейбница
Определенный
интеграл
 равен …
равен …
Решение:
Напоминаем,
что формула Ньютона – Лейбница имеет
вид:
 Тогда,
используя формулу
Тогда,
используя формулу
 ,
имеем:
,
имеем:

ЗАДАНИЕ
N 20
Тема:
Методы вычисления неопределенных
интегралов
Неопределенный
интеграл
 равен …
равен …
ЗАДАНИЕ
N 21
Тема:
Физические приложения определенного
интеграла
Скорость
движения тела задана уравнением
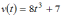 .
Тогда путь, пройденный телом за время
от первой секунды до третьей секунды
движения, равен …
.
Тогда путь, пройденный телом за время
от первой секунды до третьей секунды
движения, равен …
Решение:
Напоминаем,
что путь
 ,
пройденный телом за отрезок времени
от
,
пройденный телом за отрезок времени
от
 до
до
 ,
движущимся прямолинейно со скоростью
,
движущимся прямолинейно со скоростью
 ,
вычисляется по формуле:
,
вычисляется по формуле:
 .
Тогда,
используя условие, имеем:
.
Тогда,
используя условие, имеем:

ЗАДАНИЕ
N 22
Тема:
Свойства определенного интеграла
Определенный
интеграл
 равен …
равен …
Решение:
Обращаем
внимание, что используя свойства
интеграла
 и
и
 ,
исходный интеграл можно представить
в виде разности двух выражений и,
применяя формулу Ньютона – Лейбница
,
исходный интеграл можно представить
в виде разности двух выражений и,
применяя формулу Ньютона – Лейбница
 ,
получим:
,
получим:

ЗАДАНИЕ
N 23
Тема:
Неопределенный интеграл
Неопределенный
интеграл
 равен …
равен …
ЗАДАНИЕ
N 24
Тема:
Геометрические приложения определенного
интеграла
Площадь
фигуры, ограниченной параболой
 и
осью ОХ,
равна …
и
осью ОХ,
равна …
Решение:
Обращаем
внимание, что площадь данной плоской
фигуры вычисляется по формуле
 В
данной задаче сначала необходимо найти
пределы интегрирования (точки пересечения
параболы с осью ОХ):
В
данной задаче сначала необходимо найти
пределы интегрирования (точки пересечения
параболы с осью ОХ):
 Тогда
Тогда Площадь
фигуры равна
Площадь
фигуры равна
 (кв. ед.).
(кв. ед.).
ЗАДАНИЕ
N 25
Тема:
Раскрытие неопределенности вида
"бесконечность на бесконечность"

Решение:
Так
как
 и
и
 то
имеет место неопределенность вида
то
имеет место неопределенность вида
 Для
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на
Для
ее раскрытия нужно разделить каждое
слагаемое числителя и знаменателя на
 .
Тогда, зная, что
.
Тогда, зная, что
 получим:
получим:

ЗАДАНИЕ
N 26
Тема:
Второй замечательный предел

Решение:
Функцию
 нужно
преобразовать так, чтобы использовать
второй замечательный предел, то есть
формулу
нужно
преобразовать так, чтобы использовать
второй замечательный предел, то есть
формулу
 Для
этого числитель и знаменатель дроби
необходимо разделить на число
Для
этого числитель и знаменатель дроби
необходимо разделить на число
 ,
получим:
,
получим:
 Выполним
замену переменной, полагая, что
Выполним
замену переменной, полагая, что
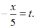 Если
Если
 ,
то и
,
то и
 ,
,
 и,
следовательно,
и,
следовательно,

ЗАДАНИЕ
N 27
Тема:
Раскрытие неопределенности вида "ноль
на ноль"

ЗАДАНИЕ
N 28
Тема:
Способы задания числовых
последовательностей
Дана
числовая последовательность
 Установите
соответствие между номером и
соответствующим членом данной
последовательности.
Установите
соответствие между номером и
соответствующим членом данной
последовательности.
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
того чтобы найти определенный член
последовательности, нужно вместо
 в
данное равенство подставить его номер.
в
данное равенство подставить его номер.




ЗАДАНИЕ
N 29
Тема:
Предел функции в точке
 …
…

 то
то
 принимает
значение, равное …
принимает
значение, равное …