
- •Составители: ст.Преп. Елена Николаевна Бесперстова
- •Порядок выполнения и защиты контрольных работ по высшей математике
- •8. Рабочая программа, теоретические сведения и методические указания для выполнения контрольных заданий указаны в методических указаниях №1540 (сокращенно м-1540). Рекомендуемая литература
- •Контрольная работа № 5
- •Примеры решения заданий для выполнения
- •Метод интегрирования по частям
- •Вычисление двойных интегралов
- •Вычисление криволинейных интегралов
- •Контрольная работа № 6 Дифференциальные уравнения
- •Примеры решения заданий контрольной работы № 6
- •Дифференциальные уравнения высших порядков
- •Уравнения, явно не содержащие неизвестной функции :
- •Уравнения, явно не содержащие независимую переменную :
- •Линейные уравнения второго порядка
- •Системы дифференциальных уравнений
Примеры решения заданий контрольной работы № 6
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Уравнения с разделяющимися переменными
Пример
25. Найти
общее решение уравнения
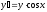 (см.
М-1540, стр. 32–33).
Имеем:
(см.
М-1540, стр. 32–33).
Имеем:
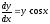 ;
;
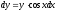 ;
;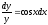 .
.
Интегрируем последнее уравнение
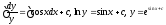 — общее решение
данного уравнения.
— общее решение
данного уравнения.
Однородные уравнения первого порядка
Пример
26. Решить
уравнение
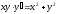 (см.
М-1540, стр. 34).
(см.
М-1540, стр. 34).
Решение.
Находим
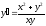 ;
;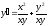 ;
;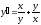 .
Так как правая часть зависит от
.
Так как правая часть зависит от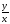 ,
то уравнение является однородным. Делаем
подстановку:
,
то уравнение является однородным. Делаем
подстановку: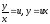 ,
тогда
,
тогда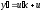 и получаем
и получаем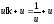 ,
,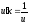 ,
,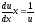 ,
,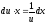 ,
,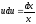 ,
интегрируя, получим
,
интегрируя, получим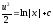 ,
,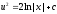 ,
,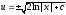 .
Следовательно,
.
Следовательно,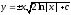 — общее решение данного уравнения.
— общее решение данного уравнения.
Линейные уравнения первого порядка
Пример
27.
Найти общее решение уравнения
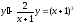 (см.
М-1540, стр. 34).
(см.
М-1540, стр. 34).
Решение.
Сделаем подстановку
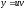 ,
где
,
где и
и — неизвестные пока функции от
— неизвестные пока функции от .
Тогда
.
Тогда
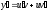 и
уравнение принимает вид:
и
уравнение принимает вид:
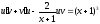 или
или
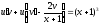 . (9)
. (9)
Выбираем
 так, чтобы
так, чтобы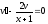 .
Решаем
это уравнение
.
Решаем
это уравнение
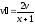 ,
,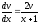 ;
;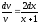 ;
интегрируя получим:
;
интегрируя получим: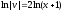 ;
;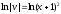 ;
;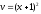 .
Подставляя это значение в равенство
(9) получим:
.
Подставляя это значение в равенство
(9) получим:
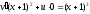 ;
;
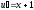 ;
;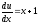 ;
;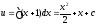 .
.
Таким
образом,
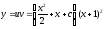 — общее решение данного уравнения.
— общее решение данного уравнения.
Замечание.
Уравнение вида
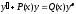 ,
при
,
при
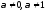 не является линейным. Оно называетсяуравнением
Бернулли,
но решается так же, как и линейное,
подстановкой
не является линейным. Оно называетсяуравнением
Бернулли,
но решается так же, как и линейное,
подстановкой
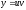 .
.
Дифференциальные уравнения высших порядков
Уравнения, не содержащие у и у′
Пример
28.
Решить дифференциальное уравнение
второго порядка
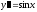 (см.
М-1540, стр. 35).
(см.
М-1540, стр. 35).
Решение.
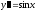 ;
;
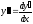 ;
;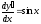 ;
;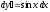 .
Интегрируя, находим
.
Интегрируя, находим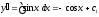 .
Далее
.
Далее
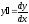 ;
;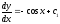 ;
;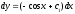 ,
интегрируя, получаем
,
интегрируя, получаем
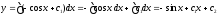 — общее решение.
— общее решение.
Замечание. Аналогичным образом решаются уравнения указанного вида более высокого порядка.
Уравнения, явно не содержащие неизвестной функции :
Пример
29.
Найти общее решение уравнения
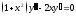 (см.
М-1540, стр. 35)
(см.
М-1540, стр. 35)
Решение.
Делаем
подстановку
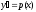 .
Тогда
.
Тогда
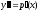 .
Получим
.
Получим
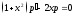 ,
,
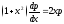 ;
;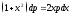 ;
;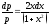 .
.
Интегрируя
последнее уравнение, найдем
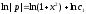 ;
;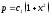 .
Так
как
.
Так
как
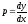 ,то
,то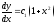 ;
;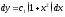 ,
откуда
,
откуда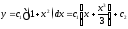 — это и есть общее решение данного
уравнения.
— это и есть общее решение данного
уравнения.
Уравнения, явно не содержащие независимую переменную :
Пример
30.
Найти общее решение уравнения
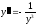 (см.
М-1540, стр. 36).
(см.
М-1540, стр. 36).
Решение.
Делая
подстановку
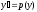 ,
,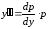 ,
получим
,
получим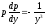 ,
,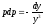 .
Интегрируем обе части уравнения:
.
Интегрируем обе части уравнения: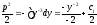 ;
;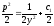 ;
;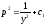 ;
;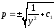 .
Так как
.
Так как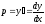 ,
то
,
то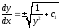 ;
;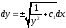 ;
;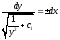 ;
;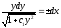 .
Интегрируя,
найдем:
.
Интегрируя,
найдем:
2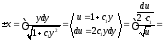
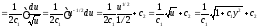 .
.
Итак,
общий
интеграл данного уравнения
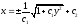 .
.
Линейные уравнения второго порядка
Пример
31. Найти
общее решение уравнения
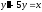 (см.
М-1540, стр. 38).
(см.
М-1540, стр. 38).
Решение.
Искомое
решение будем искать в виде
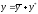 ,
где
,
где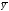 –
общее
решение уравнения
–
общее
решение уравнения
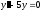 ,
ау*−
частное решение всего уравнения.
Составим
характеристическое уравнение
,
ау*−
частное решение всего уравнения.
Составим
характеристическое уравнение
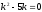 ,
,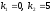 .
Следовательно,
.
Следовательно,
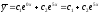 .
.
Найдем
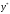 .
Так как правая часть уравнения равна
.
Так как правая часть уравнения равна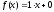 ,
то
это случай 4 табл.4 и частное решение
было бы
,
то
это случай 4 табл.4 и частное решение
было бы
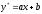 ,
если
бы числа
,
если
бы числа
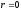 не было среди корней характеристического
уравнения. Но, так как число
не было среди корней характеристического
уравнения. Но, так как число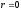 встречается среди корней характеристического
уравнения один раз (
встречается среди корней характеристического
уравнения один раз (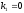 ),
то
),
то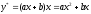 .
Найдем
.
Найдем
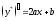 ,
,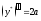 ,
подставим эти значения в данное уравнение
и потребуем, чтобы оно обратилось в
тождество
,
подставим эти значения в данное уравнение
и потребуем, чтобы оно обратилось в
тождество
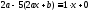 ;
;
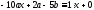 ,
,
откуда
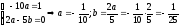 .
.
Таким
образом,
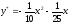 и общее решение уравнения будет
и общее решение уравнения будет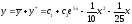 .
.
Если
в начальный момент времени
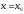 известны
известны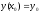 и
и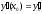 ,
то можно найти частное решение уравнения
(10), удовлетворяющее этим условиям, то
есть решить так называемуюзадачу
Коши.
,
то можно найти частное решение уравнения
(10), удовлетворяющее этим условиям, то
есть решить так называемуюзадачу
Коши.
Пример
32.
Найти
частное решение уравнения
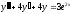 ,
удовлетворяющее
начальным условиям
,
удовлетворяющее
начальным условиям
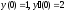 (см.
М-1540, стр. 39).
(см.
М-1540, стр. 39).
Решение.
Данное
уравнение — это уравнение вида (10), при
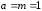 ,
,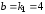 ,
,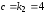 ,
,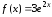 .
.
Найдем
сначала общее решение данного уравнения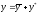 .
.
Для этого решим соответствующее однородное уравнение:
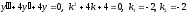 .
Следовательно
.
Следовательно
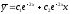 .
.
Так
как числа
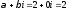 нет среди корней характеристического
уравнения, то (случай 3, табл.2) частное
решение
нет среди корней характеристического
уравнения, то (случай 3, табл.2) частное
решение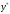 подбираем в таком же виде, как и правая
часть
подбираем в таком же виде, как и правая
часть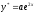 ,
,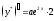 ,
,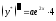 .
Подставляем
эти значения в уравнение
.
Подставляем
эти значения в уравнение
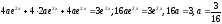 .
.
Следовательно,
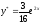 .
Значит,
.
Значит,
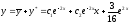 – общее решение данного уравнения. Для
нахождения частного решения,
удовлетворяющего заданным начальным
условиям, найдем:
– общее решение данного уравнения. Для
нахождения частного решения,
удовлетворяющего заданным начальным
условиям, найдем:
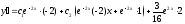 .
Так как
.
Так как
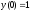 и
и
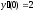 ,
то получаем
,
то получаем
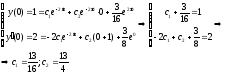
Подставляя
эти значения в общее решение, найдем
частное решение
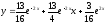 ,
удовлетворяющее заданным начальным
условиям.
,
удовлетворяющее заданным начальным
условиям.
Пример
33.
Найти частное решение уравнения
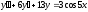 ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям: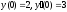 (см.
М-1540, стр. 39–40).
(см.
М-1540, стр. 39–40).
Решение.
Данное уравнение — это уравнение вида
(10), при
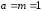 ,
,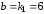 ,
,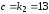 ,
,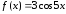 .
.
Решаем
уравнение
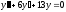 .
Составляем
характеристическое уравнение
.
Составляем
характеристическое уравнение
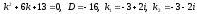 .
.
Следовательно,
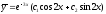 – общее решение уравнения без правой
части. По виду правой части
– общее решение уравнения без правой
части. По виду правой части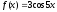 находим число
находим число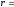
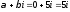 (случай 2, табл. 2). Такого числа среди
корней характеристического уравнения
нет, поэтому
(случай 2, табл. 2). Такого числа среди
корней характеристического уравнения
нет, поэтому
( )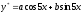 ;
;
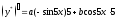 ;
;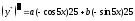 .
Подставим
эти значения в данное уравнение
.
Подставим
эти значения в данное уравнение
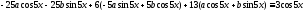 или
или
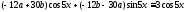 .
Сравнивая
слагаемые, содержащие
.
Сравнивая
слагаемые, содержащие
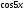 и
и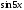 ,
получим
,
получим
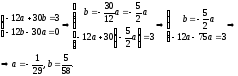
Поэтому
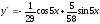 ,
,
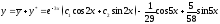 – общее решение данного уравнения.
Найдем
– общее решение данного уравнения.
Найдем
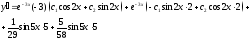
Учитывая
начальные условия, найдем:
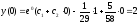 ,
,
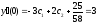 ,откуда
,откуда
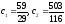 .
Подставляя эти значения в общее решение,
получим
.
Подставляя эти значения в общее решение,
получим
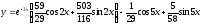 — частное
решение исходного уравнения, удовлетворяющее
заданным начальным условиям.
— частное
решение исходного уравнения, удовлетворяющее
заданным начальным условиям.
Физический
смысл полученного решения (и предыдущих)
в том, что это есть отклонение платформы
от положения равновесия в любой момент
времени. В частности, при
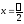 получим
получим
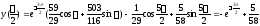 .
.
