
- •Составители: ст.Преп. Елена Николаевна Бесперстова
- •Порядок выполнения и защиты контрольных работ по высшей математике
- •8. Рабочая программа, теоретические сведения и методические указания для выполнения контрольных заданий указаны в методических указаниях №1540 (сокращенно м-1540). Рекомендуемая литература
- •Контрольная работа № 5
- •Примеры решения заданий для выполнения
- •Метод интегрирования по частям
- •Вычисление двойных интегралов
- •Вычисление криволинейных интегралов
- •Контрольная работа № 6 Дифференциальные уравнения
- •Примеры решения заданий контрольной работы № 6
- •Дифференциальные уравнения высших порядков
- •Уравнения, явно не содержащие неизвестной функции :
- •Уравнения, явно не содержащие независимую переменную :
- •Линейные уравнения второго порядка
- •Системы дифференциальных уравнений
Вычисление двойных интегралов
Пример
21. Вычислить
двойной интеграл двумя способами,
изменяя порядок интегрирования:
 ,
гдеD
— область, ограниченная линиями
,
гдеD
— область, ограниченная линиями
 ,
, ,
, (см.
М-1540, стр.52–55).
(см.
М-1540, стр.52–55).
Решение. Сделаем чертеж (рис. 4)

рис. 4
Выбирая
внутреннее интегрирование по переменной
 ,
а внешнее по
,
а внешнее по ,
получим:
,
получим:
 .
.
Здесь
внешний интеграл берется по переменной
 .
Граничными точками этой переменной
будут точки
.
Граничными точками этой переменной
будут точки и
и ,
которые и определяют внешние пределы
интегрирования. Внутренний интеграл
берется по переменной
,
которые и определяют внешние пределы
интегрирования. Внутренний интеграл
берется по переменной .
Пределы интегрирования для него будут
являться функциями от
.
Пределы интегрирования для него будут
являться функциями от ,
которые определяются из уравнений
линий, ограничивающих областьD
снизу (
,
которые определяются из уравнений
линий, ограничивающих областьD
снизу ( )
и сверху (
)
и сверху ( ).
Следовательно,
).
Следовательно,

Изменяя
порядок интегрирования, разобьем область
D
на две части: пусть D1
— часть, лежащая ниже оси
 ,
аD2
— часть, лежащая выше оси
,
аD2
— часть, лежащая выше оси
 .
Тогда
.
Тогда
 .
.

Совпадение результатов подтверждает правильность вычислений.
.
Вычисление криволинейных интегралов
Пример 22.
Вычислить криволинейный интеграл
 ,если
кривая АВ
задана уравнением
,если
кривая АВ
задана уравнением
 и
и (см.
М-1540, стр. 57–58).
(см.
М-1540, стр. 57–58).
Решение.
Так как кривая задана явным уравнением
 ,
где
,
где ,
то
вычисляем интеграл по формуле (16). Находим
,
то
вычисляем интеграл по формуле (16). Находим
 и
и

Пример
23.
Вычислить криволинейный интеграл
 от точкиМ(1,1)
до точки N(4,2)
вдоль кривой
от точкиМ(1,1)
до точки N(4,2)
вдоль кривой
 .
.
Решение. Этот интеграл вычисляем по формуле (17)

Пример
24.
Вычислить криволинейный интеграл
 ,
если криваяАВ
задана параметрическими уравнениями:
,
если криваяАВ
задана параметрическими уравнениями:
 ,
, ,
, .
.
Решение. Кривая АВ есть часть эллипса с полуосями 3 и 2, находящаяся в первой четверти. Так как кривая АВ задана параметрически, то этот интеграл будем вычислять по формуле (18). Имеем

Замечание. Если в криволинейном интеграле путь интегрирования L разбит на несколько участков, например, на L1 и L2, то
 =
= +
+ .
.
Контрольная работа № 6 Дифференциальные уравнения
7. Найдите общее решение дифференциальных уравнений
|
7.1. |
a)
b)
c)
|
7.2. |
a)
b)
c)
|
|
7.3. |
a)
b)
c)
|
7.4. |
a)
b)
c)
|
|
7.5. |
a)
b)
c)
|
7.6. |
a)
b)
c)
|
|
7.7. |
a)
b)
c)
|
7.8. |
a)
b)
c)
|
|
7.9. |
a)
b)
c)
|
7.10. |
a)
b)
c)
|
|
7.11. |
a)
b)
c)
|
7.12. |
a)
b)
c)
|
|
7.13. |
a)
b)
c)
|
7.14. |
a)
b)
c)
|
|
7.15. |
a)
b)
c)
|
7.16. |
a)
b)
c)
|
|
7.17. |
a)
b)
c)
|
7.18. |
a)
b)
c)
|
|
7.19. |
a)
b)
c)
|
7.20. |
a)
b)
c)
|
|
7.21. |
a)
b)
c)
|
7.22. |
a)
b)
c)
|
|
7.23. |
a)
b)
c)
|
7.24. |
a)
b)
c)
|
|
7.25. |
a)
b)
c)
|
7.26. |
a)
b)
c)
|
|
7.27. |
a)
b)
c)
|
7.28. |
a)
b)
c)
|
|
7.29. |
a)
b)
c)
|
7.30. |
a)
b)
c)
|
8. Найдите общее решение однородных дифференциальных уравнений.
|
8.1 |
a)
b)
c)
|
8.2. |
a)
b)
c)
|
|
8.3. |
a)
b)
c)
|
8.4. |
a)
b)
c)
|
|
8.5. |
a)
b)
c)
|
8.6. |
a)
b)
c)
|
|
8.7. |
a)
b)
c)
|
8.8. |
a)
b)
c)
|
|
8.9. |
a)
b)
c)
|
8.10. |
a)
b)
c)
|
|
8.11. |
a)
b)
c)
|
8.12. |
a)
b)
c)
|
|
8.13. |
a)
b)
c)
|
8.14. |
a)
b)
c)
|
|
8.15. |
a)
b)
c)
|
8.16. |
a)
b)
c)
|
|
8.17. |
a)
b)
c)
|
8.18. |
a)
b)
c)
|
|
8.19. |
a)
b)
c)
|
8.20. |
a)
b)
c)
|
|
8.21. |
a)
b)
c)
|
8.22. |
a)
b)
c)
|
|
8.23. |
a)
b)
c)
|
8.24. |
a)
b)
c)
|
|
8.25. |
a)
b)
c)
|
8.26. |
a)
b) y″−12y′−36y=0; c)
|
|
8.27. |
a)
b)
c)
|
8.28. |
a)
b)
c)
|
|
8.29. |
a)
b)
c)
|
8.30. |
a)
b)
c)
|
9.
Железнодорожная
платформа массой m,
выведенная из положения равновесия,
совершает колебания в вертикальной
плоскости под действием вынуждающей
силы
 ,
гдех
— время. Найдите зависимость отклонения
платформы от положения равновесия
,
гдех
— время. Найдите зависимость отклонения
платформы от положения равновесия
 от времени, если сопротивление среды
пропорционально скорости, с коэффициентом
пропорциональности
от времени, если сопротивление среды
пропорционально скорости, с коэффициентом
пропорциональности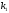 ,
а восстанавливающая сила рессоры,
стремящаяся вернуть платформу в положение
равновесия, пропорциональна величине
отклонения, с коэффициентом
пропорциональности
,
а восстанавливающая сила рессоры,
стремящаяся вернуть платформу в положение
равновесия, пропорциональна величине
отклонения, с коэффициентом
пропорциональности .
Считается, что в момент времени
.
Считается, что в момент времени ,
, ,
, .
.
Таблица 3
|
№ |
m |
|
|
|
|
|
|
9.1 |
1 |
-2 |
2 |
|
|
|
|
9.2 |
1 |
-6 |
9 |
|
|
|
|
9.3 |
1 |
-1 |
0 |
|
|
|
|
9.4 |
1 |
2 |
-3 |
|
|
|
|
9.5 |
1 |
4 |
5 |
|
|
|
|
9.6 |
1 |
0 |
-4 |
|
|
|
|
9.7 |
1 |
2 |
1 |
|
|
|
|
9.8 |
1 |
-3 |
-4 |
|
|
|
|
9.9 |
1 |
0 |
-9 |
|
|
|
|
9.10 |
1 |
5 |
0 |
|
|
|
|
9.11 |
1 |
-2 |
1 |
|
|
|
|
9.12 |
1 |
0 |
4 |
|
|
|
|
9.13 |
1 |
6 |
-16 |
|
|
|
|
9.14 |
1 |
3 |
0 |
|
|
|
|
9.15 |
1 |
-3 |
4 |
|
|
|
|
9.16 |
1 |
-6 |
13 |
|
|
|
|
9.17 |
1 |
4 |
20 |
|
|
|
|
9.18 |
1 |
1 |
0 |
|
|
|
|
9.19 |
1 |
0 |
-16 |
|
|
|
|
9.20 |
1 |
-4 |
5 |
|
|
|
|
9.21 |
1 |
5 |
-6 |
|
|
|
|
9.22 |
1 |
3 |
-4 |
|
|
|
|
9.23 |
1 |
9 |
0 |
|
|
|
|
9.24 |
1 |
0 |
1 |
|
|
|
|
9.25 |
1 |
7 |
-8 |
|
|
|
|
9.26 |
1 |
-6 |
5 |
|
|
|
|
9.27 |
1 |
-25 |
0 |
|
|
|
|
9.28 |
1 |
0 |
16 |
|
|
|
|
9.29 |
1 |
-5 |
4 |
|
|
|
|
9.30 |
1 |
0 |
4 |
|
|
|
8. Дана система дифференциальных уравнений

С помощью характеристического уравнения найти ее общее решение.
Таблица 4
|
№ |
a |
b |
c |
d |
№ |
a |
b |
c |
d |
|
10.1 |
-1 |
5 |
1 |
3 |
10.2 |
-2 |
1 |
-3 |
2 |
|
10.3 |
6 |
3 |
-8 |
-5 |
10.4 |
2 |
1 |
-6 |
3 |
|
10.5 |
2 |
5 |
1 |
2 |
10.6 |
6 |
-1 |
3 |
2 |
|
10.7 |
-7 |
5 |
4 |
-8 |
10.8 |
-1 |
2 |
-3 |
4 |
|
10.9 |
-1 |
1 |
2 |
-2 |
10.10 |
-1 |
-2 |
3 |
4 |
|
10.11 |
-1 |
-2 |
1 |
4 |
10.12 |
-2 |
1 |
4 |
1 |
|
10.13 |
3 |
-2 |
1 |
0 |
10.14 |
4 |
2 |
4 |
6 |
|
10.15 |
-5 |
-8 |
-3 |
-3 |
10.16 |
8 |
-3 |
2 |
1 |
|
10.17 |
-4 |
2 |
4 |
-2 |
10.18 |
3 |
1 |
1 |
3 |
|
10.19 |
-3 |
6 |
2 |
8 |
10.20 |
2 |
3 |
5 |
4 |
|
10.21 |
2 |
1 |
3 |
4 |
10.22 |
1 |
2 |
3 |
6 |
|
10.23 |
1 |
-1 |
-4 |
1 |
10.24 |
5 |
4 |
4 |
5 |
|
10.25 |
-1 |
8 |
1 |
1 |
10.26 |
1 |
-2 |
-4 |
3 |
|
10.27 |
-2 |
-3 |
-1 |
0 |
10.28 |
1 |
-2 |
-1 |
0 |
|
10.29 |
1 |
-1 |
-4 |
4 |
10.30 |
3 |
-2 |
2 |
8 |

 ;
; ;
; .
. ;
;
 ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
;
 ;
; ;
;
 .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; ;
; .
.








 1
1

 0
0 0
0
 -0,3
-0,3 1
1
 1
1 -1
-1
 0
0 0
0
 0
0 0
0
 4
4 0
0
 -2
-2 2
2
 1
1 0
0
 0
0 0
0
 0
0 0
0
 1
1 1
1
 0
0 -1
-1
 1
1 1
1
 0
0 0
0
 0
0 0
0
 -2
-2 1
1
 0
0 0
0
 0
0 0
0
 1
1 -1
-1
 0
0 0
0
 0
0 0
0
 0
0 0
0
 1
1 -1
-1
 2
2 3
3
 3
3 -1
-1
 0
0 0
0
 0
0 0
0
 4
4 0
0