- •Составители: ст.Преп. Елена Николаевна Бесперстова
- •Порядок выполнения и защиты контрольных работ по высшей математике
- •8. Рабочая программа, теоретические сведения и методические указания для выполнения контрольных заданий указаны в методических указаниях №1540 (сокращенно м-1540). Рекомендуемая литература
- •Контрольная работа № 5
- •Примеры решения заданий для выполнения
- •Метод интегрирования по частям
- •Вычисление двойных интегралов
- •Вычисление криволинейных интегралов
- •Контрольная работа № 6 Дифференциальные уравнения
- •Примеры решения заданий контрольной работы № 6
- •Дифференциальные уравнения высших порядков
- •Уравнения, явно не содержащие неизвестной функции :
- •Уравнения, явно не содержащие независимую переменную :
- •Линейные уравнения второго порядка
- •Системы дифференциальных уравнений
Примеры решения заданий для выполнения
контрольной работы № 5
Таблица 1
Основные правила и формулы интегрирования
|
1. |
|
10. |
|
|
2. |
|
11. |
|
|
3. |
|
12. |
|
|
4. |
|
13.
|
|
|
5. |
|
14. |
|
|
6. |
|
15. |
|
|
7. |
|
16. |
|
|
8. |
|
17. |
|
|
9. |
|
18. |
|
|
|
|
19. |
|
В формулах 3 – 19 переменная u может быть как независимой переменной, так и некоторой функцией аргумента x.
НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ
Пример
1.
Найти интеграл
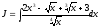 (см. М-1540, стр. 12–13).
(см. М-1540, стр. 12–13).
Решение. Преобразуем подынтегральное выражение и воспользуемся формулами 1, 2, 4. Получим
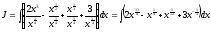 .
.
Здесь
мы применили известные формулы
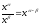 и
и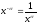 .
Следовательно,
.
Следовательно,
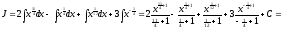
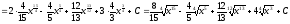 .
.
Проверим найденный результат дифференцированием. Найдем
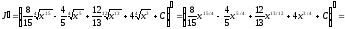
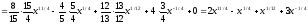 ,
,
что совпадает с подынтегральным выражением, и, следовательно, интегрирование проведено правильно.
МЕТОД ПОДСТАНОВКИ ИЛИ ЗАМЕНЫ ПЕРЕМЕННОЙ
Пример
2.
Вычислить интеграл
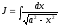 (см. М-1540, стр. 14).
(см. М-1540, стр. 14).
Решение.
Сделаем
подстановку
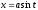 ,
тогда
,
тогда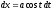 и
и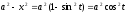 .
Поэтому интеграл преобразуется к виду
.
Поэтому интеграл преобразуется к виду
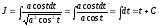 .
.
Из
подстановки
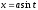 найдем
найдем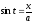 и
и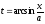 .
Тогда
.
Тогда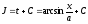 .
.
Таким образом, мы получили табличный интеграл
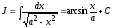 .
.
Пример
3.
Вычислить интеграл
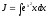 (см. М-1540, стр. 14).
(см. М-1540, стр. 14).
Решение.
Сделаем
подстановку
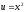 .
Тогда
.
Тогда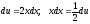 .
Переходя под интегралом к переменной
.
Переходя под интегралом к переменной ,
получим
,
получим
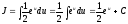 .
.
Возвращаясь
к переменной
 ,
найдем окончательно
,
найдем окончательно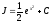 .
.
Сделаем
проверку
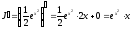 ,
что совпадает с подынтегральным
выражением.
,
что совпадает с подынтегральным
выражением.
Аналогичным образом вычислим еще несколько интегралов, не делая подробных объяснений.
Пример
4.
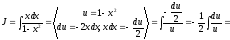
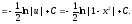
Пример
5.
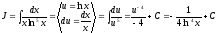 .
.
Пример
6.
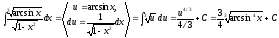 .
.
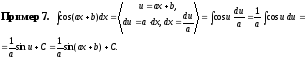
Пример
8.
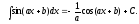
Метод интегрирования по частям
Пример
9.
Вычислить интеграл
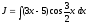 (см. М-1540, стр. 15).
(см. М-1540, стр. 15).
Решение.
Обозначим
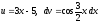 .
Тогда
.
Тогда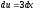 ,
а
,
а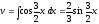 (см. пример 7), по формуле (3) получим
(см. пример 7), по формуле (3) получим
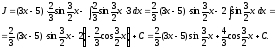
Пример
10.
Вычислить интеграл
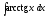 (см. М-1540, стр. 15).
(см. М-1540, стр. 15).
Решение.

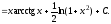 (см. пример 4).
(см. пример 4).
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Пример
11. Вычислить
интеграл
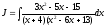 (см.
М-1540, стр. 16–18).
(см.
М-1540, стр. 16–18).
Решение.
Представим
подынтегральную дробь в виде суммы
простейших дробей. Так как квадратный
трехчлен
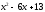 имеет отрицательный дискриминант
имеет отрицательный дискриминант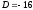 ,
то
,
то
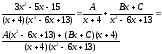
Отсюда получаем
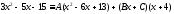 ,
,
или
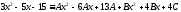 ,
,
или
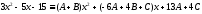 .
.
Приравнивая
коэффициенты при одинаковых степенях
 в левой и правой частях, получим:
в левой и правой частях, получим:
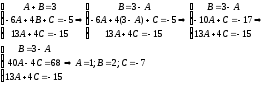
Таким образом,
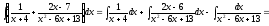
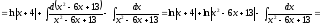
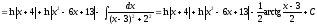 .
.
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
Пример
12.
Вычислить интеграл
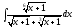 (см.
М-1540, стр. 18–19).
(см.
М-1540, стр. 18–19).
Решение.
Так
как
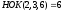 ,
сделаем подстановку
,
сделаем подстановку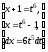 .
Тогда
.
Тогда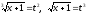 и
и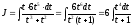 .
.
Разделив
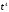 на
на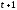 ,
получим
,
получим
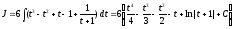 ,
где
,
где
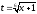 .
.
Следовательно,
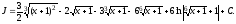
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Пример
13. Вычислить
интеграл
 (см.
М-1540, стр. 19).
(см.
М-1540, стр. 19).
Решение.
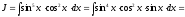
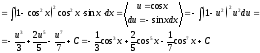
Пример
14.
Вычислить интеграл
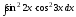 (см.
М-1540, стр. 19).
(см.
М-1540, стр. 19).
Решение.
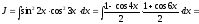
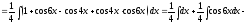
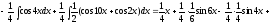
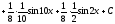 .
.
Пример
15. Вычислить
интеграл
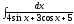 (см.
М-1540, стр. 19).
(см.
М-1540, стр. 19).
Решение.
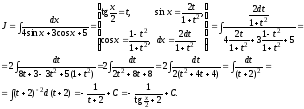
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример 16. Вычислить определенный интеграл
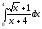 (см.
М-1540, стр. 20–21).
(см.
М-1540, стр. 20–21).
Решение.
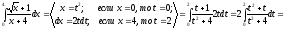
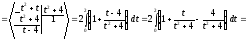
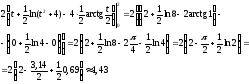
При вычислении этого интеграла были применены формулы
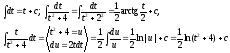
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Несобственные интегралы по бесконечному промежутку
Пример
17.
Вычислить несобственный интеграл
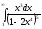 или доказать его расходимость (см.
М-1540, стр. 23).
или доказать его расходимость (см.
М-1540, стр. 23).
Решение.
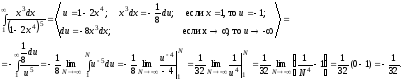
Таким
образом, несобственный интеграл равен
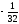 ,
т. е. он сходится.
,
т. е. он сходится.
Несобственные интегралы второго рода
Пример
18.
Вычислить интеграл
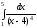 или доказать его расходимость.
(см.
М-1540, стр.23–24).
или доказать его расходимость.
(см.
М-1540, стр.23–24).
Решение.
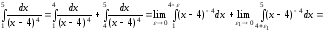

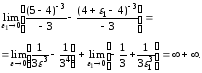
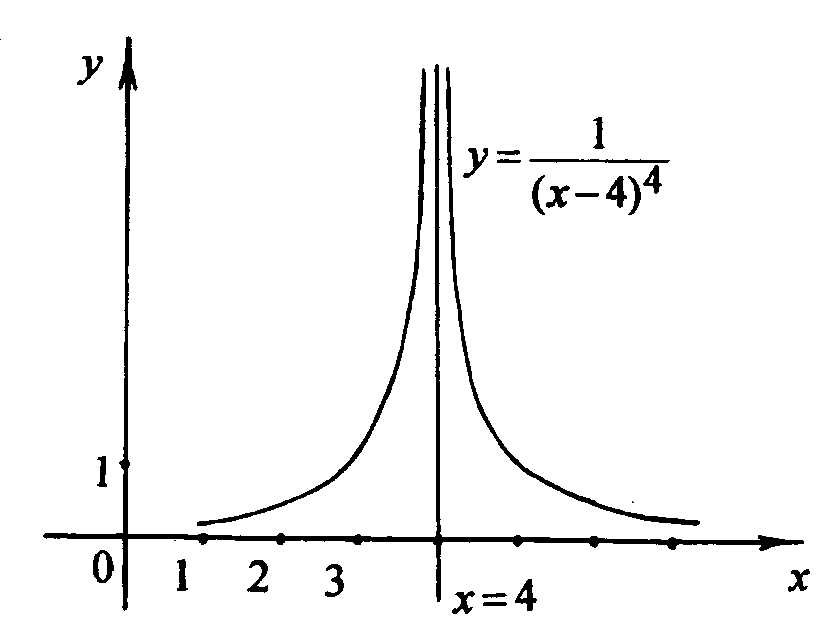
Так как оба предела стремятся к бесконечности, то они не существуют и поэтому, несобственный интеграл расходится (рис. 1).
рис.
1
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пример
19.
Найти площадь фигуры, ограниченной
линиями
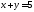 ,
,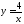 (см. М-1540, стр.24–25).
(см. М-1540, стр.24–25).
Решение. Первое уравнение определяет на плоскости прямую линию, второе – гиперболу (рис. 2).
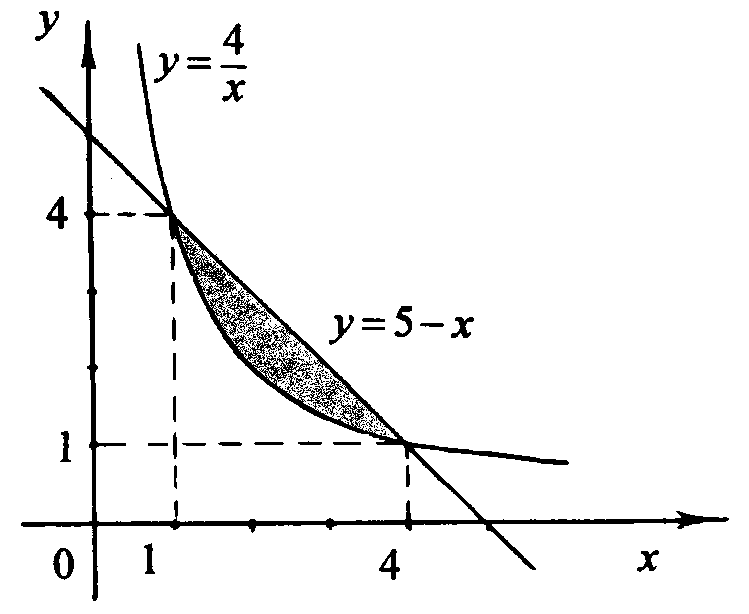
рис. 2
Найдем их точки пересечения
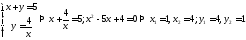
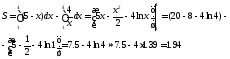
Пример
20.
Вычислить площадь области, ограниченной
кривой, уравнение которой в полярной
системе координат имеет вид
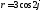 ,
,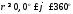 (см. М-1540, стр.26).
(см. М-1540, стр.26).
Решение.
Для построения кривой составим таблицу значений функции.
Таблица 2
|
|
0 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
150 |
165 |
180 |
|
|
3 |
2,55 |
1,5 |
0 |
- |
- |
- |
- |
- |
0 |
1,5 |
2,55 |
3 |
Для
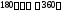 значения
значения будут повторяться в силу периодичности
функции
будут повторяться в силу периодичности
функции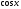 .
Строим кривую по точкам (нижняя часть
кривой симметрично достраивается) (рис.
3).
.
Строим кривую по точкам (нижняя часть
кривой симметрично достраивается) (рис.
3).

рис. 3
Заметим, что построенная фигура состоит из четырех равных частей, поэтому
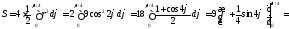
 (кв.ед.)
(кв.ед.)

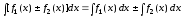 ;
;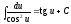 ;
;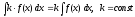 ;
;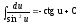 ;
;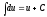 ;
;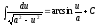 ;
;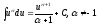 ;
;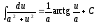 ;
;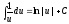 ,
,
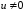 ;
;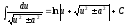 ;
;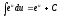 ;
;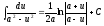 ;
; ;
; ;
; ;
; ;
;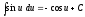 ;
;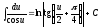 ;
;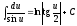 .
.