Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ZADANIYa_1_semestr.docx

Скачиваний:

Добавлен:

09.04.2015

Размер:

2.97 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

Функции многих переменных

Задание 34. Дана функция 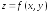. Найдите: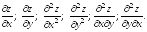

1. ;	11	21 ;
2. ;	12. ;	22 ;
3. ;	13 ;	23 ;
4. ;	14. ;	24 ;
5. ;	15 ;	25 ;
6. ;	16 ;	26 ;
7. ;	17 ;	27 ;
8. ;	18 ;	28 ;
9. ;	19 ;	29 ;
10.	20 ;	30 ;

Задание 35. Дана функция 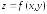, точка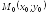и вектор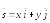. Найдите градиент функции и производную по направлению векторав точке.

1. ;	;
2. ;	;
3. ;	;
4. ;	;	.
5. ;	;	.
6. ;	;	.
7. ;	;	.
8. ;	;
9. ;	;	.
10. ;	;	.
11. ;	;	.
12 .;	;	.
13. ;	;	.
14. ;	;	.
15. ;	;	.
16. ;	;	.
17. ;		.
18. ;	;	.
19. ;	;	.
20. ;	;	.
21. ;	;	.
22. ;	;	.
23. ;	;	.
24. ;	;	.
25. ;	;
26. ;	;	.
27. ;	;	.
28. ;	;	.
29. ;	;	.
30. ;	;	.

Задание 36. Найти наибольшее и наименьшее значения функции z=f(x,y) в области D, заданной системой неравенств. Сделать чертеж области D.

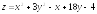; D: .
; D: .
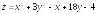; D: .
; D: .
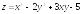; D: .
; D: .
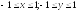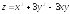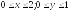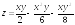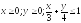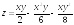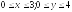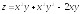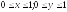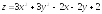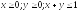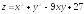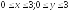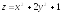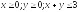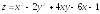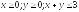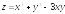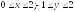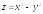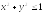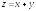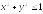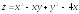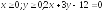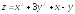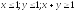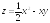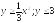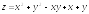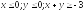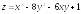; D: .
; D: .
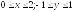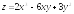; D: .
; D: .
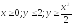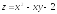; D: .
; D: .
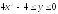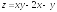; D: .
; D: .
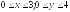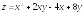; D: .
; D: .
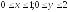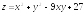; D: .
; D: .
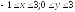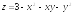; D: .
; D: .
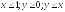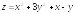; D: .
; D: .
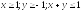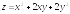; D: .
; D: .
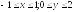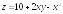; D: .
; D: .
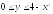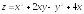; D: .
; D: .
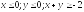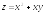; D: .
; D: .

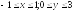Задание 37. Экспериментально получены значения искомой функции 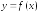при нескольких значениях аргумента. Считая зависимость междуx и y линейной, найдите методом наименьших квадратов приближенное уравнение функции в виде 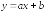. Сделайте чертеж.

1	x	1	2	3	4	5	6	7	8	9
1	y	4,3	5,3	3,8	1,8	2,3	1,2	0,9	-0,2	-1,1
2	x	1	2	3	4	5	6	7	8	9
2	y	1,0	3,2	5,5	6,8	8,5	10,5	12,7	14,0	16,2
3	x	1	2	3	4	5	6	7	8	9
3	y	-0,5	-3,2	-5,5	-7,2	-9,5	-11,5	-13,2	-14,8	-17,3
4	x	1	2	3	4	5	6	7	8	9
4	y	4,1	7,0	9,8	13,1	15,8	19,0	22,1	24,7	28,2

5	x	1	2	3	4	5	6	7	8	9
5	y	2,2	0,8	0,1	-1,2	-2,0	-3,1	-3,9	-5,2	-6,1
6	x	1	2	3	4	5	6	7	8	9
6	y	0,1	1,8	4,2	5,9	8,1	9,7	12,3	14,0	16,1
7	x	1	2	3	4	5	6	7	8	9
7	y	3,5	4,2	4,4	5,2	5,7	6,2	6,5	7,2	7,6
8	x	1	2	3	4	5	6	7	8	9
8	y	1,2	3,8	7,1	9,9	13,2	15,7	19,0	21,8	25,2
9	x	1	2	3	4	5	6	7	8	9
9	y	2,2	6,5	9,0	13,5	16,1	19,5	23,7	27,4	30,2
10	x	1	2	3	4	5	6	7	8	9
10	y	-2,1	0,2	2,2	4,3	6,5	7,8	10,5	11,5	14,2
11	x	1	2	3	4	5	6	7	8	9
11	y	0,9	4,3	5,9	7,5	9,6	12,4	13,3	15,6	19,3
12	x	1	2	3	4	5	6	7	8	9
12	y	0	-0,6	-1,6	-1,8	-2,4	-3,4	-3,3	-4,2	-5
13	x	1	2	3	4	5	6	7	8	9
13	y	-0,7	-1,2	-2,8	-3,9	-5,2	-5,8	-7,4	-7,9	-9,8
14	x	1	2	3	4	5	6	7	8	9
14	y	2,5	3,7	5,1	5,9	6,8	8,3	8,9	9,9	10,9
15	x	1	2	3	4	5	6	7	8	9
15	y	3,4	4,5	6,2	7,1	7,9	9,4	9,9	11,3	12,3
16	x	1	2	3	4	5	6	7	8	9
16	y	-0,8	0,1	1,4	2,2	3,2	3,9	5,3	6,1	7,5
17	x	1	2	3	4	5	6	7	8	9
17	y	0,2	1,5	1,9	2,6	4,1	5,2	6,3	7,1	8,4
18	x	1	2	3	4	5	6	7	8	9
18	y	0,2	-0,8	-1,9	-3,2	-3,8	-4,8	-6,4	-6,8	-8,5
19	x	1	2	3	4	5	6	7	8	9
19	y	1,1	-0,2	-1,1	-1,9	-3,1	-3,9	-5,1	-6,3	-7,3
20	x	1	2	3	4	5	6	7	8	9
20	y	2,1	0,7	-0,1	-1,2	-2,3	-3,2	-4,2	-4,9	-6,3
21	x	1	2	3	4	5	6	7	8	9
21	y	-2,5	-1,2	0,3	1,3	2,4	3,2	3,7	5,6	6,2

22	x	1	2	3	4	5	6	7	8	9
22	y	1,9	1,1	-0,3	-1,5	-2,5	-3,0	-3,9	-5,1	-6,5
23	x	1	2	3	4	5	6	7	8	9
23	y	-2,1	-1,5	0,3	1,7	2,5	3,1	4,1	5,8	6,5
24	x	1	2	3	4	5	6	7	8	9
24	y	0,1	-1,1	-2,3	-3,5	-4,3	-5,3	-6,2	-7,4	-8,1
25	x	1	2	3	4	5	6	7	8	9
25	y	1,5	-0,5	-1,6	-2,5	-3,2	-4,3	-5,1	-5,9	-8,1
26	x	1	2	3	4	5	6	7	8	9
26	y	1,1	2,6	4,9	7,5	9,5	11,2	11,9	15,6	18,3
27	x	1	2	3	4	5	6	7	8	9
27	y	1,3	-1,2	-3,5	-5,1	-6,4	-9,1	-10,4	-13,5	-15,3
28	x	1	2	3	4	5	6	7	8	9
28	y	3,5	2,5	1,1	0,1	-0,8	-1,9	-3,5	-3,9	-5,6
29	x	1	2	3	4	5	6	7	8	9
29	y	4,1	3,2	2,1	1,2	0,3	-1,1	-2,6	-2,9	-4,1
30	x	1	2	3	4	5	6	7	8	9
30	y	0,6	0,1	-0,3	-2,3	-3,2	-4,3	-4,9	-6,1	-7,5

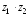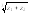Задание 38. Даны комплексные числа z₁ и z₂ (табл. 6). Записать их в тригонометрической форме. Найти числа ,z₁/ z₂, . Все результаты записать в тригонометрической и алгебраической формах. Отметить полученные числа на комплексной плоскости.

№ варианта	z₁	z₂	№ варианта	z₁	z₂
1.	,	.	16.	,	.
2.	3 + 3i,	.	17.	– 4 + 4i,	.
3.	,	.	18.	,	.
4.	,	.	19.	,	.
5.	– 2 + 2i,	.	20.	3 – 3i,	.
6.	,	.	21.	,	.
7.	,	.	22.	,	.
8.	– 4 – 4i,	.	23.	2 – 2i,	.
9.	,	.	24.	,	.
10.	,	.	25.	,	.
11.	1 – i,	.	26.	1 + i,	.
12.	,	.	27.	,	.
13.	,	.	28.	,	.
14.	2 + 2i,	.	29.	– 5 + 5i,	.
15.	,	.	30.	,	.
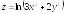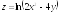
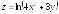
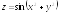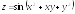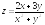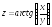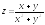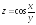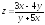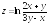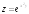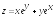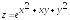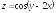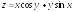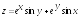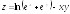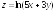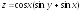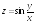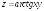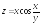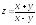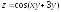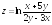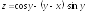
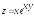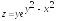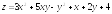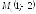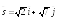
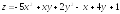
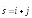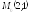
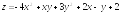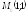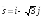
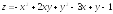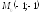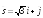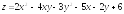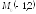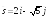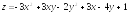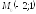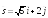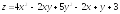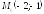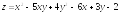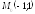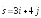
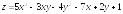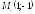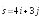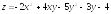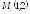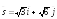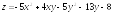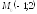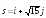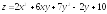
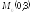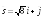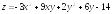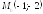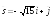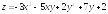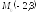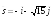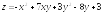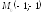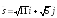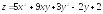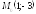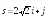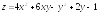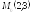
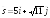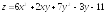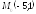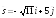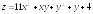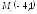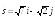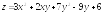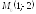
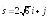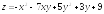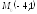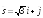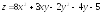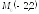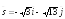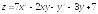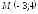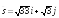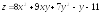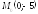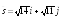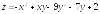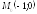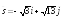
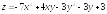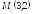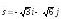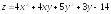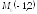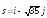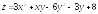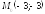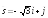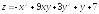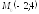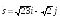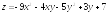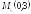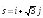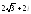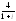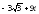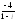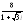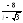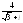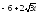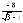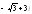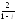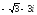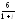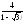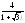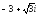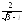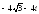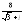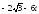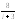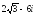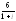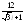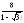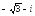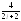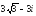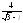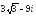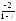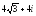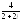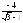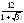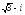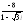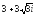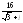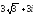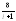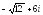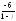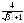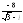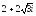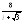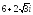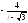