А) методом Гаусса
б) методом Жордана-Гаусса.
Решение:
а) Решаем методом Гаусса. Запишем расширенную матрицу системы:
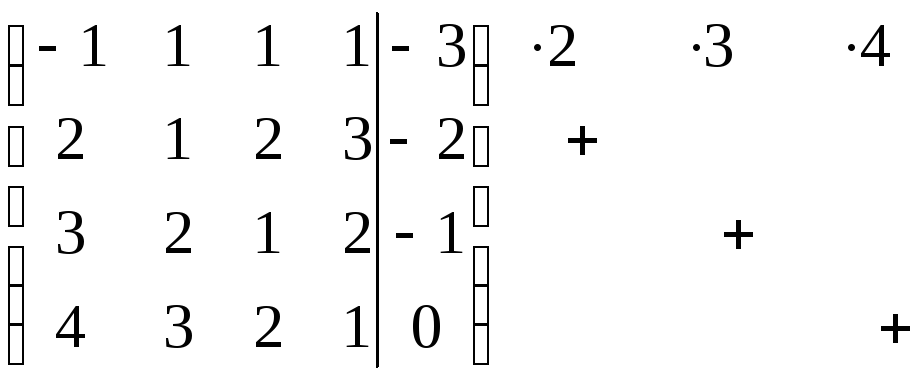
1шаг:
Элементы первой строки умножаем на 2 и сложим с соответствующими элементами 2-й строки, затем элемент 1-й строки умножим на 3 и сложим с 3-й строкой, умножим на 4 и сложим с 4-й строкой. Получим эквивалентную матрицу:
~
~
2 шаг.
Поменяем местами 2-й и 4-й столбцы, отметим, в эквивалентной матрице какой переменной соответствуют столбцы.
~
~
3 шаг.
Умножим элементы 2-й строки на (-1) и сложим с элементами 3-й и 4-й строк.
~
~
4 шаг.
Поменяем местами 3-ю и 4-ю строки
~
теперь уже точно система приведена к треугольному виду.
Обратный ход:
Проверка. Подставим найденные значения в исходную систему.
получим тождества
Ответ:
б) Решим систему методом Жордана-Гаусса.
Запишем расширенную матрицу системы
~
1 шаг.
Умножим элементы 1-й строки на (-3) сложим с элементами 2-й строки; потом на (-2) сложим с элементами 3-й строки; затем на (-1) и сложим с элементами 4-й строки, получим эквивалентную матрицу:
~
~
2 шаг.
Всю 2-ю строку разделим на (-1). Сложим элементы второй строки с элементами первой и четвертой строк и затем сложим с элементами 3-й строки:
~
~
~
3 шаг.
Умножим
элементы 3-й строки на
и сложим с элементами 2-й строки, затем
просто сложим элементы 3-й строки с
элементами 1-й строки, получим эквивалентную
матрицу:
~
~
4 шаг.
Разделим
4-ю строку на 10; затем умножим на 5 и сложим
с элементами второй строки, умножим
элементы 4-й строки на
и сложим с элементами 1-й строки. Получим
эквивалентную матрицу:
~
.
получаем
ответ:
Задание 3.2. Решить системы линейных алгебраических уравнений
а) Методом Гаусса
б) Методом Жордана-Гаусса.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Пример
3.3. Решить систему линейных уравнений
,
заданную расширенной матрицей, методом
последовательного исключения неизвестных.
В случае неопределенности системы найти
ее общее, базисное и любое частное
решение. Сделать проверку.
Решение:
Решаем задачу методом Жордана-Гаусса:
~
~
~
~
~
~
~
~
Нулевую строку вычеркиваем.
Система
неопределенная
.
Базисными
переменными являются:
Выражая базисные переменные, через свободные, получаем общее решение системы линейных уравнений:
Приравнивая свободные переменные к нулю, получаем базисное решение:
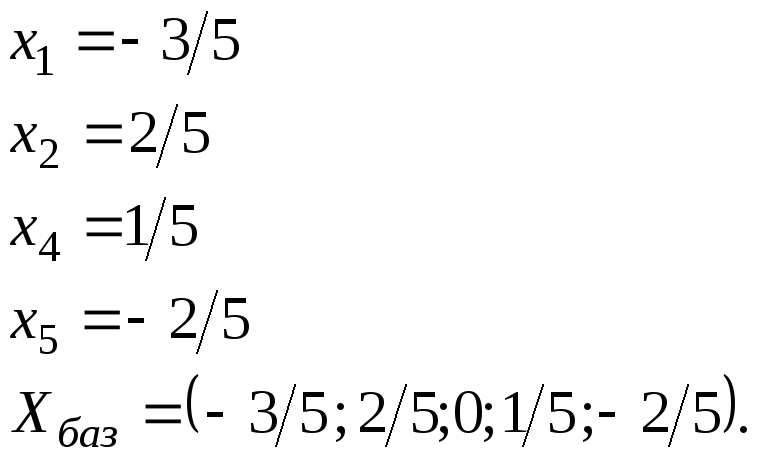
Задавая в общем, решении свободным переменным произвольные значения, получим частное решение:
Например,
если
,
то
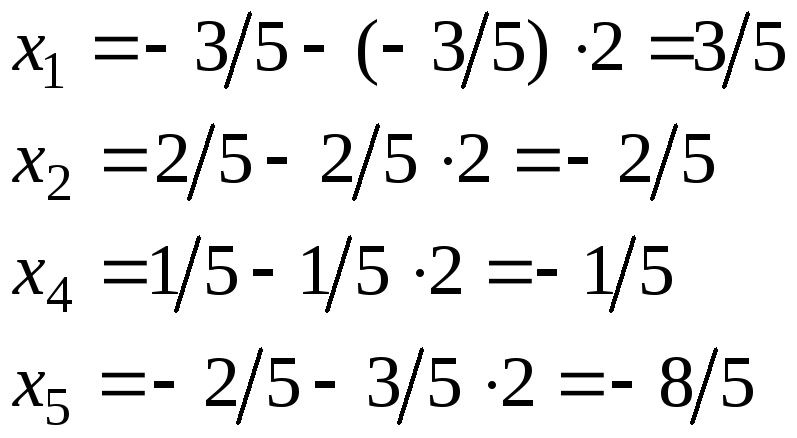
Делаем проверку, подставляя частное решение в систему линейных уравнений:
Ответ:
Общее
решение: 
Базисное
решение: 
Частное
решение: 
Задание 3.3. Решить систему линейных уравнений методом последовательного исключения неизвестных (методом Гаусса). Найти общее решение, базисное решение, частное решение. Сделать проверку.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;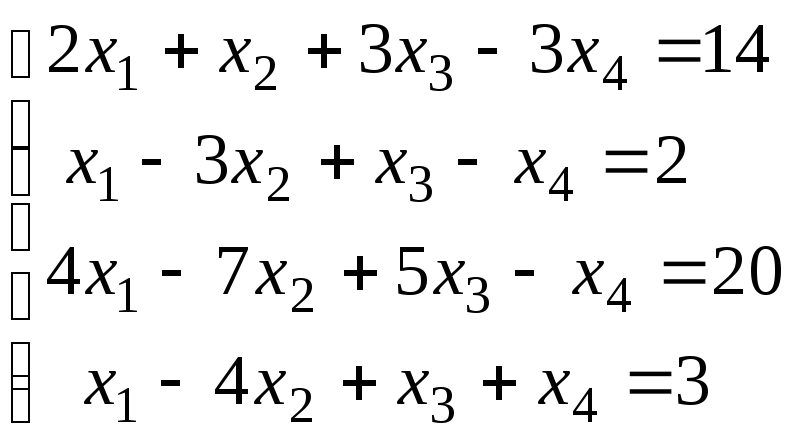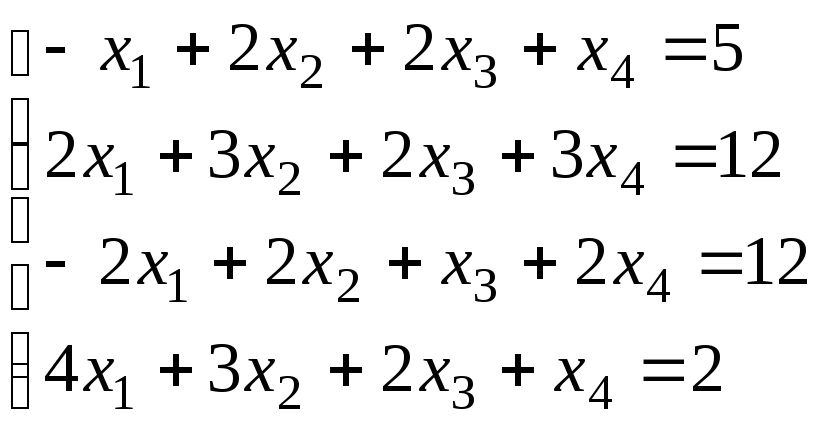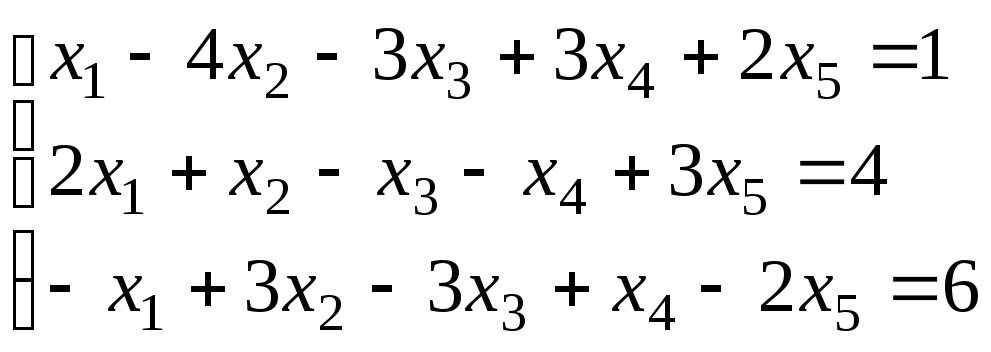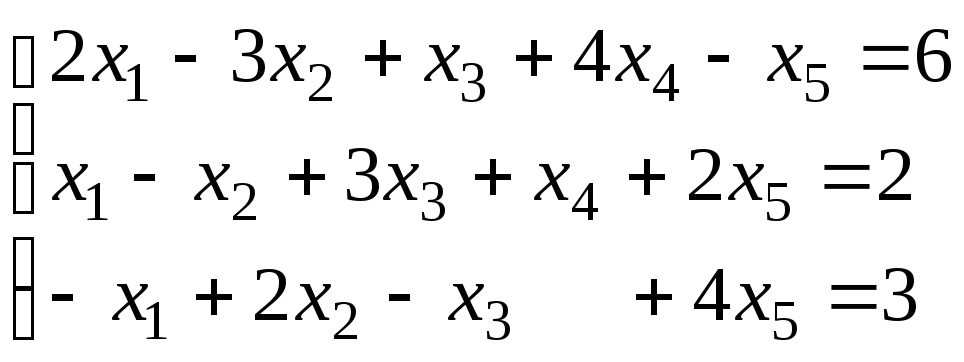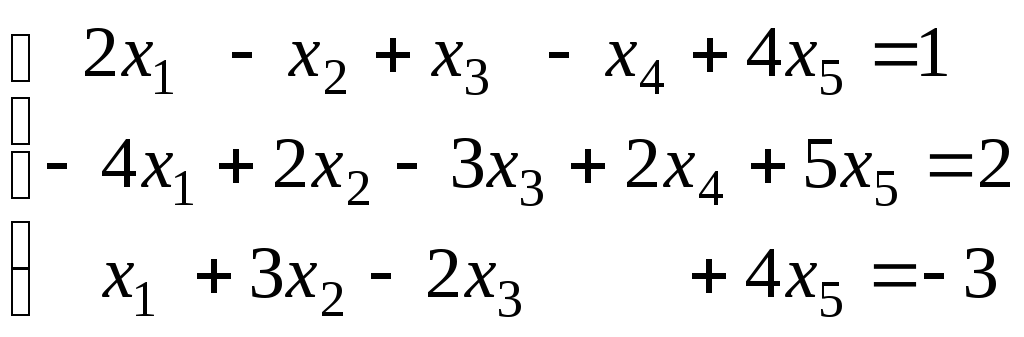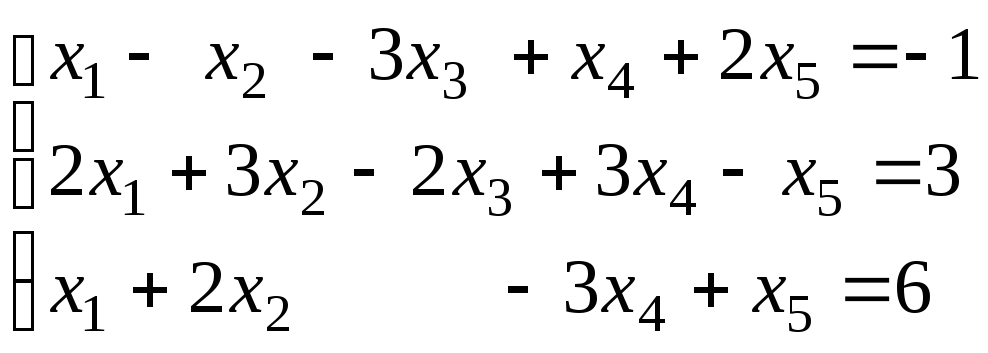