Задания

Задание 1.1. Вычислить определитель третьего порядка:

а) по определению (по правилу треугольников);

б) по правилу Саррюса;

в) по правилу Фридерищева;

г) разложением по элементам i-й строки;

д) разложением по элементам j-го столбца;

е) получив нули в любой строке или любом столбце;

ж) преобразовав его к треугольному виду.

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

1.11

1.12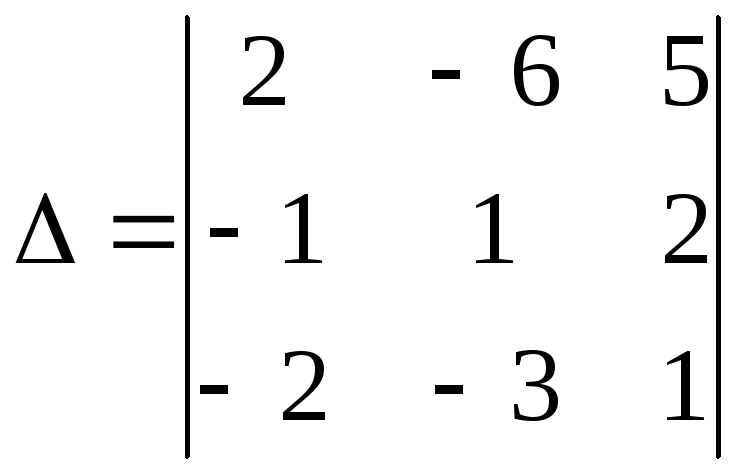

1.13

1.14

1.15

1.16

1.17

1.18

1.19

1.20

1.21

1.22

1.23

1.24

1.25

1.26

1.27

1.28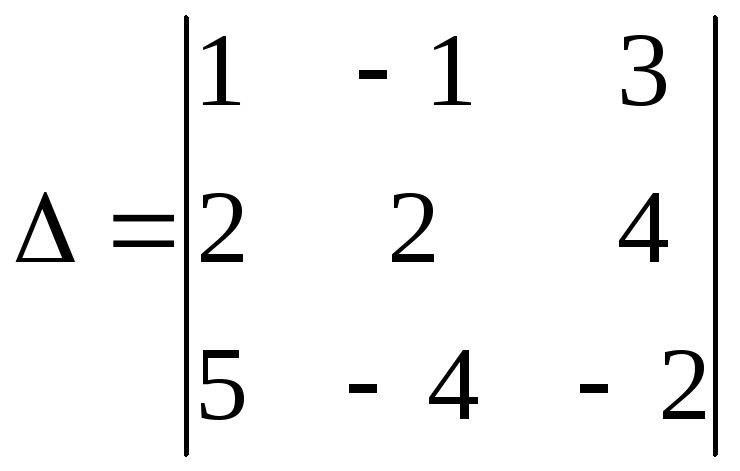

1.29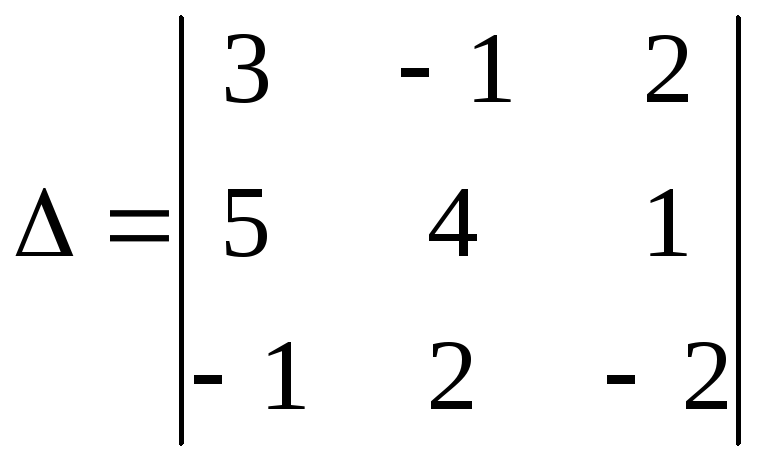

1.30

Задание 1.2. Вычислить определитель четвертого порядка:

а) получив нули в i-й строке;

б) получив нули в j-й столбце;

в) преобразовав его к треугольному виду.

2.1

2.2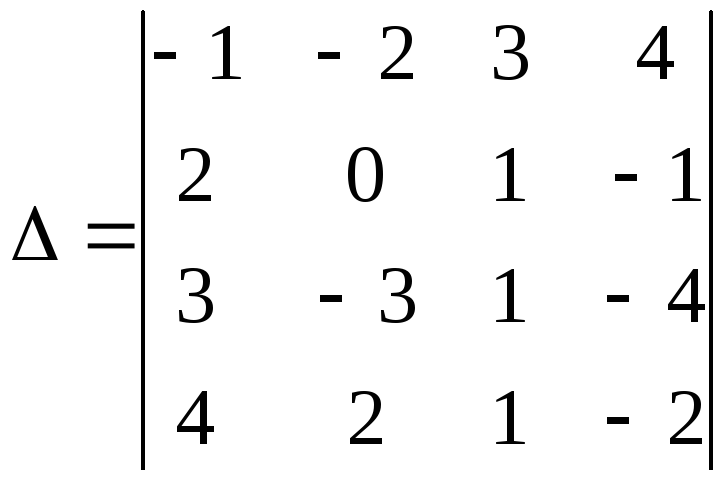

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18

2.19

2.20

2.21

2.22

2.23

2.24

2.25

2.26

2.27

2.28

2.29

2.30

2. Матрицы

0. Матрицы и операции над ними

Прямоугольная таблица, составленная из элементовнекоторого множества, называетсяматрицейи записывается в виде:

или

Индексы элемента:

- номер строки, - номер столбца.

Матрицы обозначают прописными буквами латинского алфавита Размерность матрицы, где- число строк;- число столбцов. Краткая запись:.

Матрица называется числовой, если её элементы- числа;функциональной, если- функции;векторной, если- векторы и т.д.

Если - матрица квадратная;

- матрица прямоугольная;

при - матрица-строка (или вектор-строка);

при - матрица-столбец (или вектор-столбец);

Квадратная матрица, по главной диагонали которой стоят единицы, а все остальные элементы равны нулю, называется единичнойи обозначается . Единичная матрица обладает свойством:

.

Матрицы равны тогда и только тогда, когда они имеют одинаковую размерность и соответствующие элементы совпадают.

Линейные операции над матрицами

1. Умножение матрицы на число. Чтобы умножить матрицу на число, нужно все элементы матрицы умножить на это число.

2. Сложение и вычитание матриц. Эти операции определяются только для матриц одинаковой размерности.

Суммой (разностью) матрици, обозначаемой() называется матрица, элементы которой().

Например. Найти линейную операцию,

если ,.

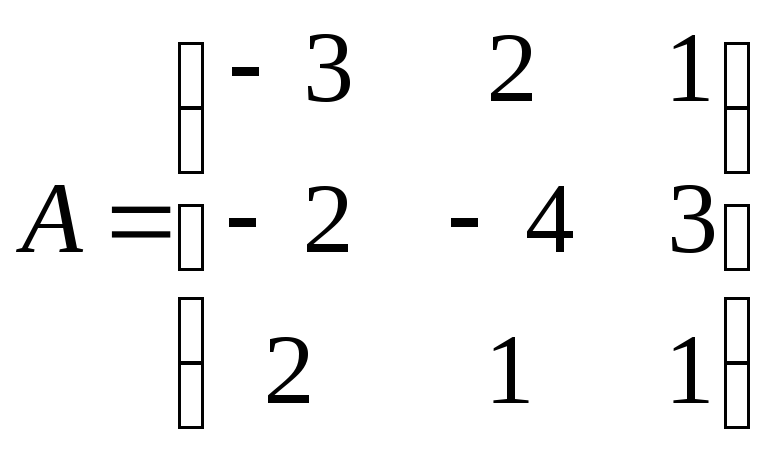Итак, согласно первому и второму пунктам:

3. Умножение матриц. Эта операция не относиться к линейной.

Произведением матриц иназывается матрица(проще записывается), элементы которой

,

где ,- элементы матрици- соответственно.

Отсюда следует, что произведение существует только в случае, когда первый множительимеет числостолбцовравное числустроквторого множителя.

Далее, число строк матрицы равно числустрок, а число столбцов – числустолбцов.

Из существования произведения не следует существования произведения.Как правило,. Если, то матрицыиназываютсяперестановочными(иликоммутирующими). Известно, что всегда.

Например. Даны матрицыи. Найтии.

(выполняется, так как число столбцовравно числу строк)

(выполняется, так как число столбцовравно числу строк)