Задания
Найти пределы функций.
1.1. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.2. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.3. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.4. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.5. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.6. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.7. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.8. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.9. а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.10 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.11 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.12 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.13 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.14 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.15 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.16 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.17 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.18 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.19 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.20 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.21 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.22 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.23 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.24 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.25 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.26 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.27 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.28 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.29 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
1.30 а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
Найти односторонние пределы функции
в точке разрыва. Указать вид точки
разрыва. Построить график функции.
2.1 а)
; б)
;
2.2 а)
; б)
;
2.3 а)
; б)
;
2.4 а)
; б)
;
2.5 а)
; б)
;
2.6 а)
; б)
;
2.7 а)
; б)
;
2.8 а)
; б)
;
2.9 а)
; б)
;
2.10 а)
; б)
;
2.11 а)
; б)
;
2.12 а)
; б)
;
2.13 а)
; б)
;
2.14 а)
; б)
;
2.15 а)
; б)
;
2.16 а)
; б)
;
2.17 а)
; б)
;
2.18 а)
; б)
;
2.19 а)
; б)
;
2.20 а)
; б)
;
2.21 а)
; б)
;
2.22 а)
; б)
;
2.23 а)
; б)
;
2.24 а)
; б)
;
2.25 а)
; б)
;
2.26 а)
; б)
;
2.27 а)
; б)
;
2.28 а)
; б)
;
2.29 а)
; б)
;
2.30 а)
; б)
;
Исследовать данную функцию на непрерывность и построить ее график.
3.1 
;
3.2 
;
3.3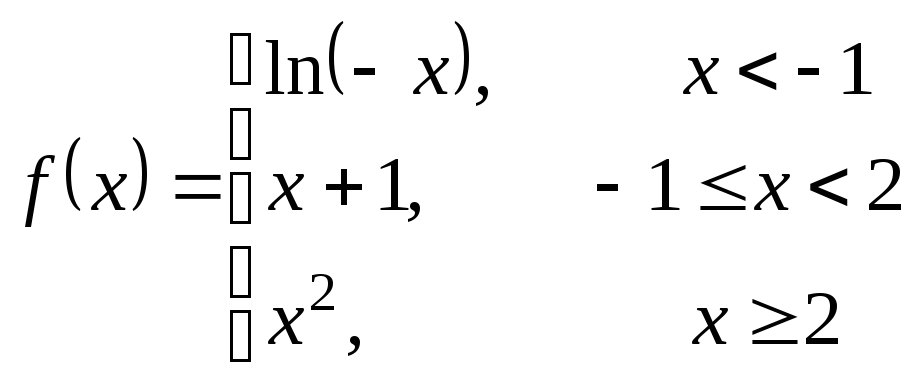 
;
3.4 
;
3.5 
;
3.6 
;
3.7 
3.8 
;
3.9 
;
3.10 
;
3.11 
;
3.12 
;
3.13 
;
3.14 
;
3.15 
;
3.16 
;
3.17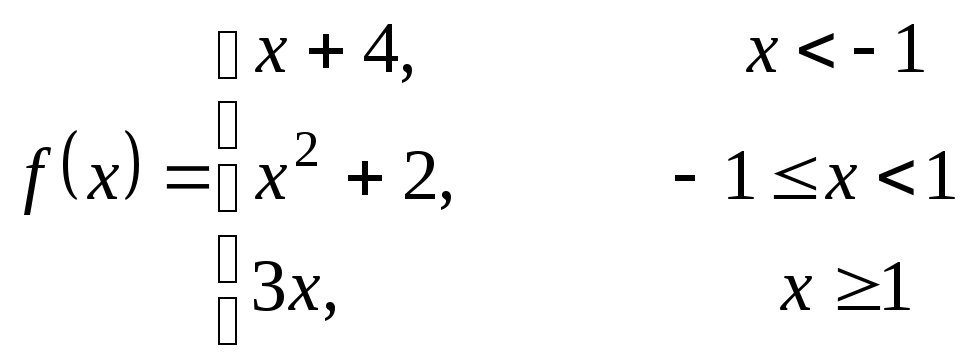 
;
3.18 
;
3.19 
;
3.20 
;
3.21 
;
3.22 
;
3.23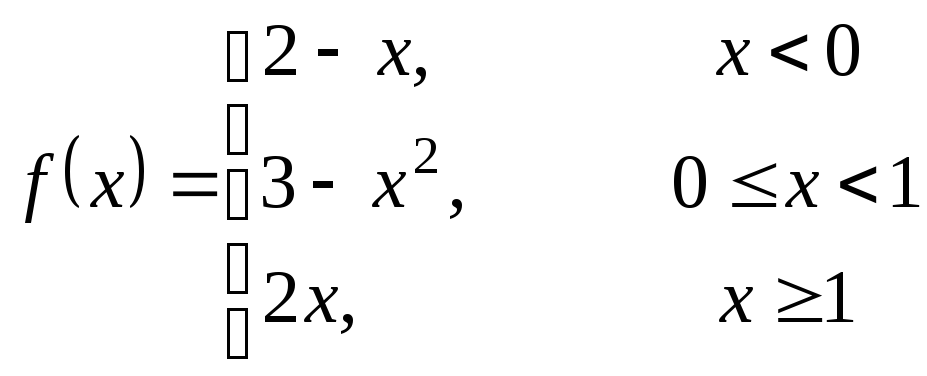 
;
3.24 
;
3.25 
; 3.26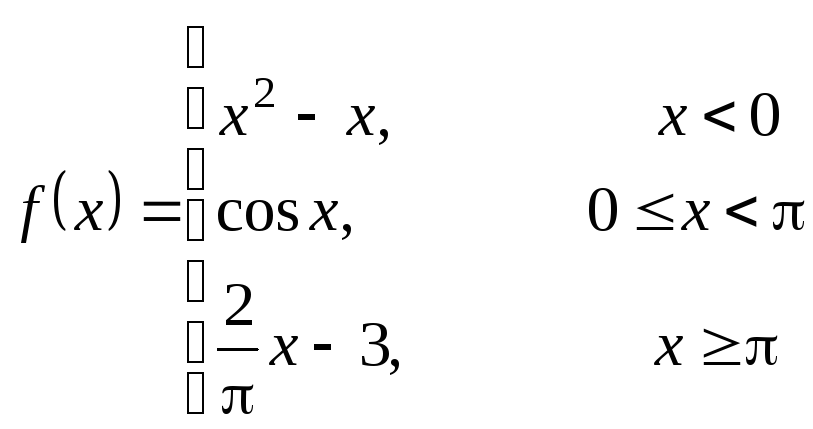
;
3.27 
;
3.28 
;
3.29 
;
3.30 
.
Найти указанные пределы, решив номера
,
,
,
,
,
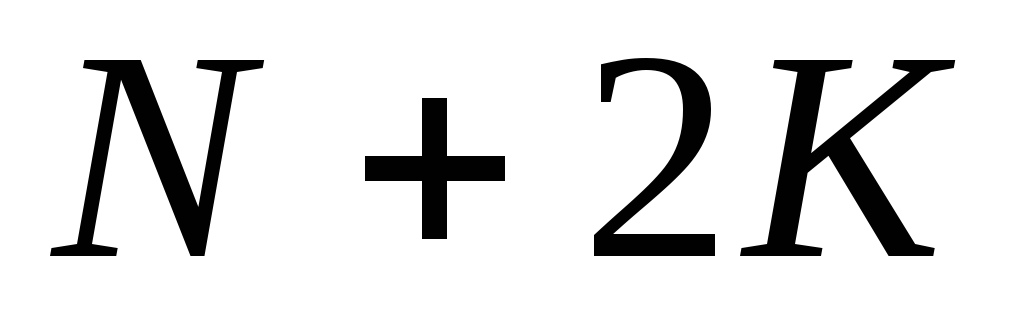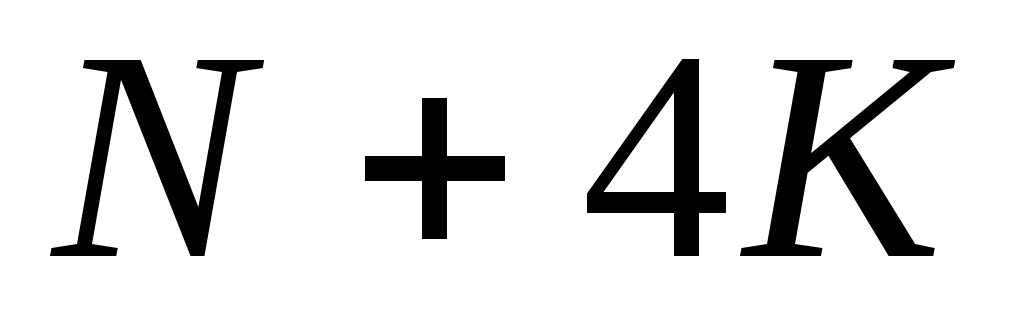где
- порядковый номер студента в группе,
- число студентов в группе. Проверить
правильность решения, сравнив его с
ответом.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
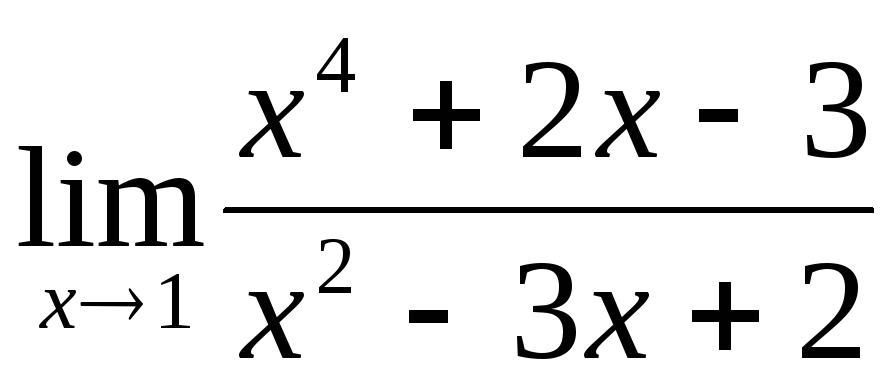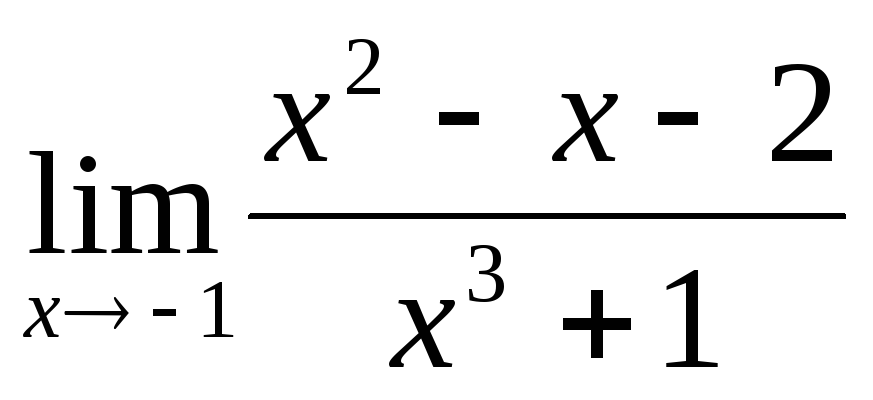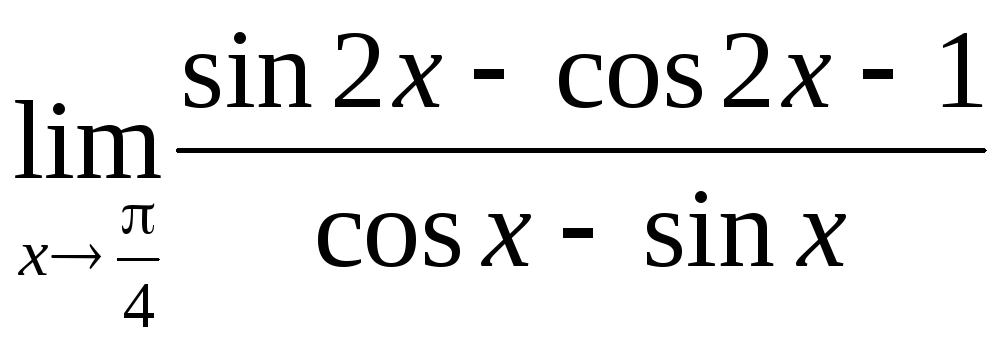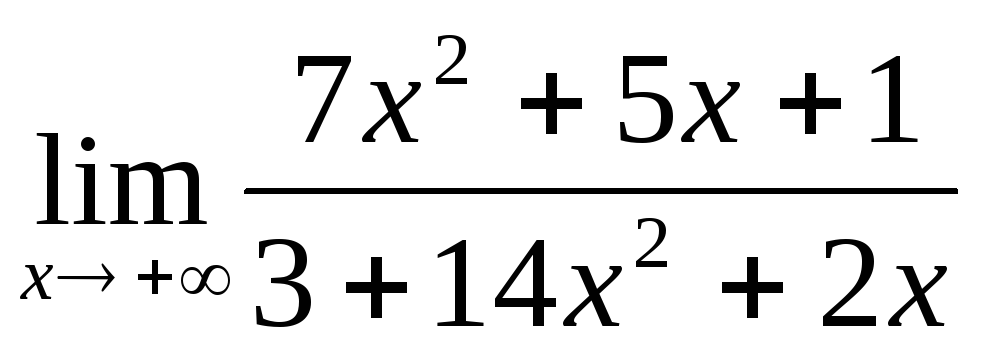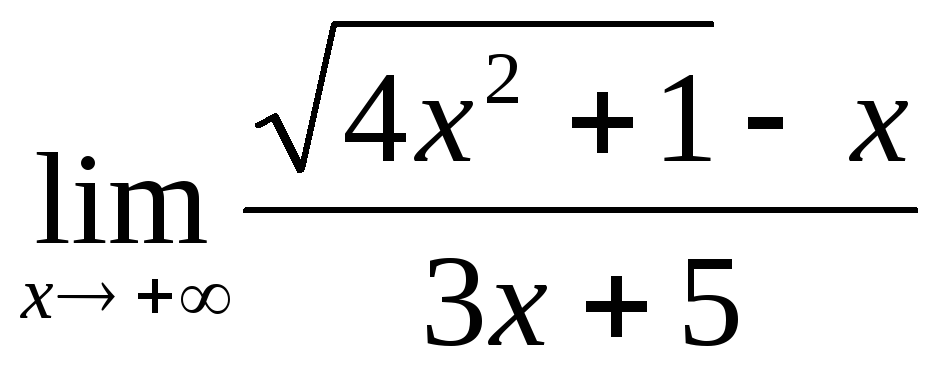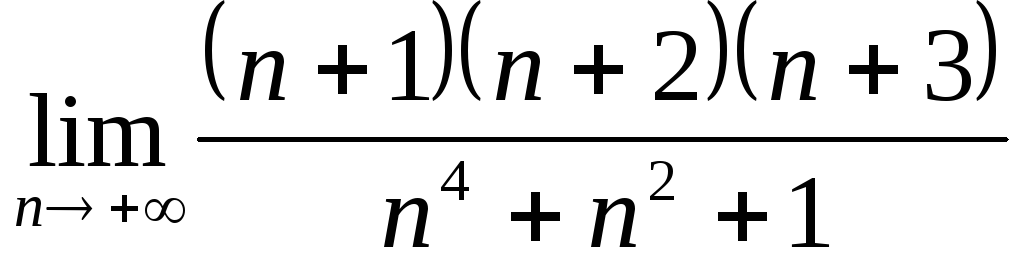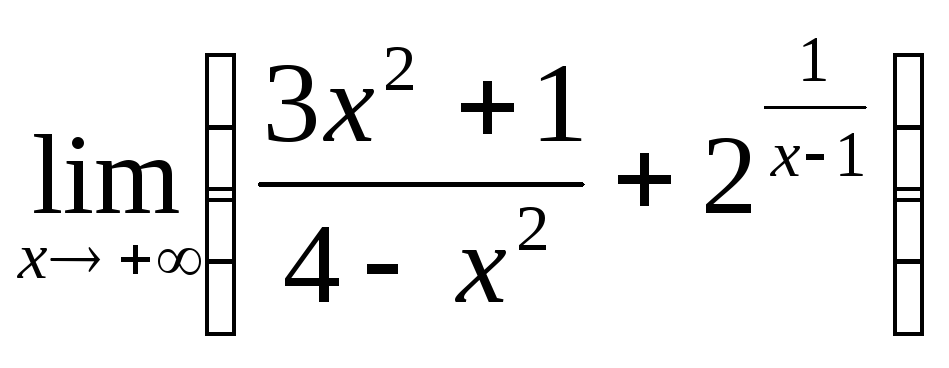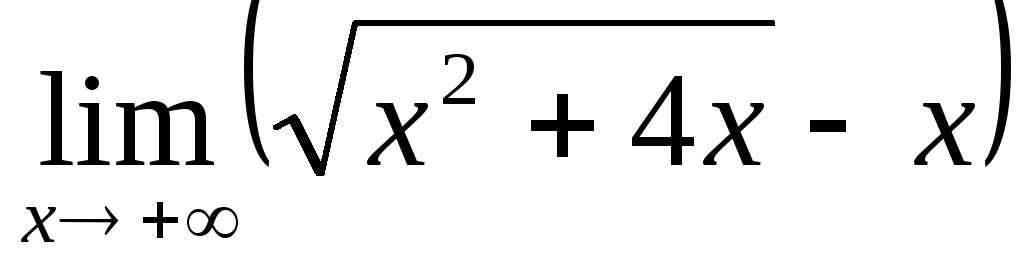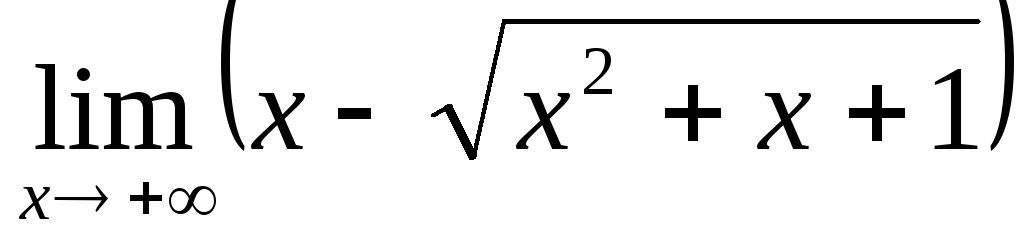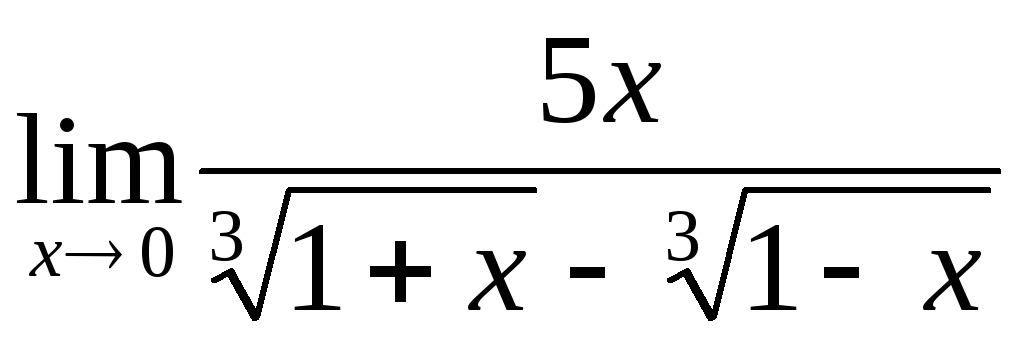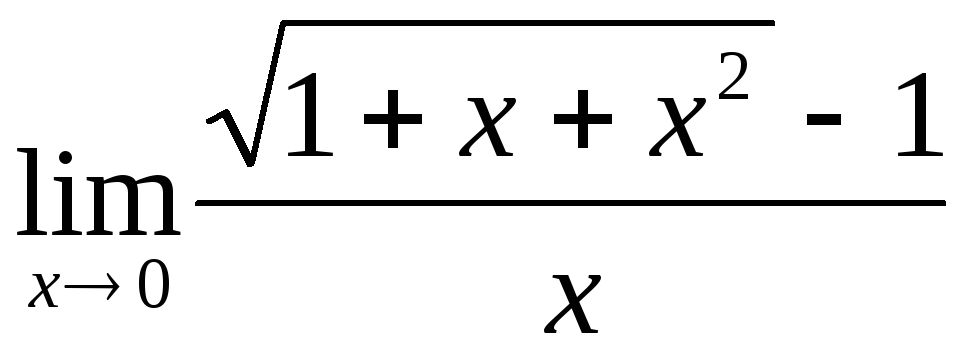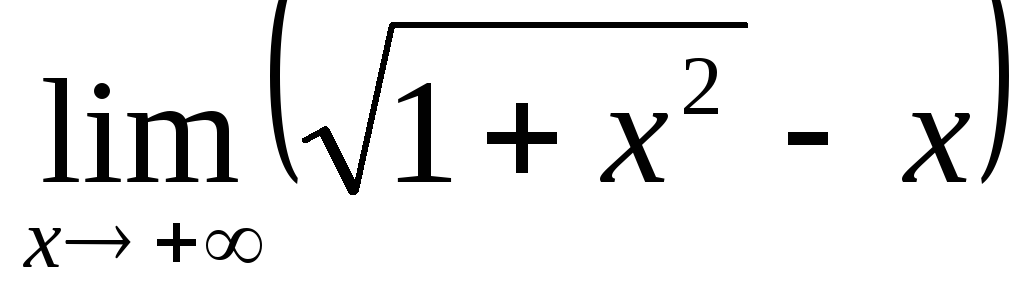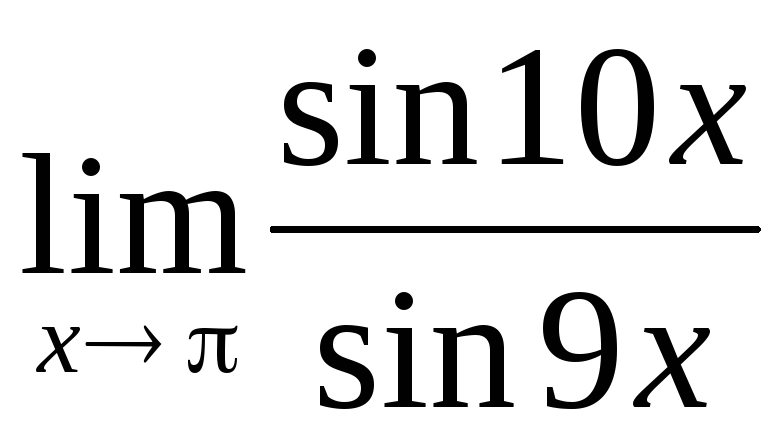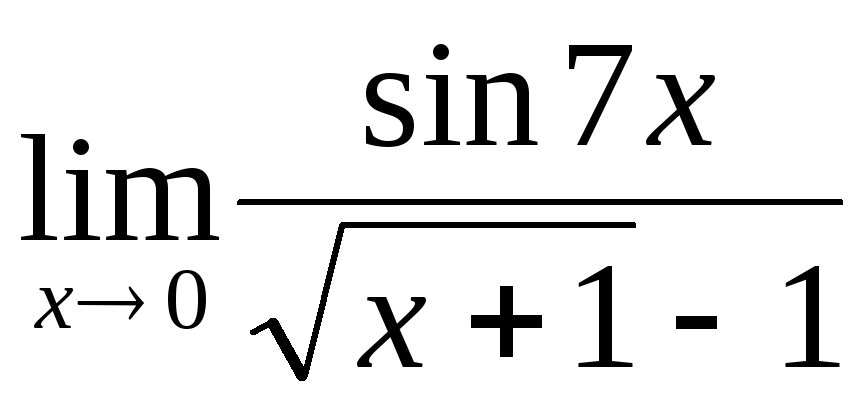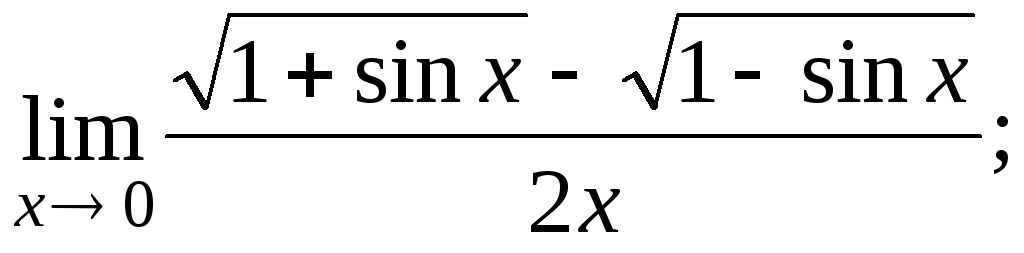
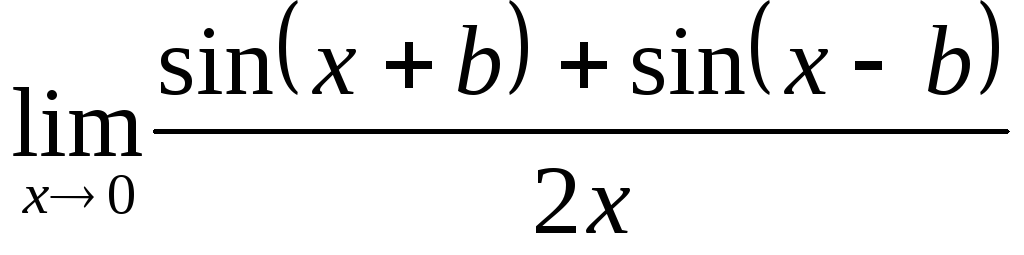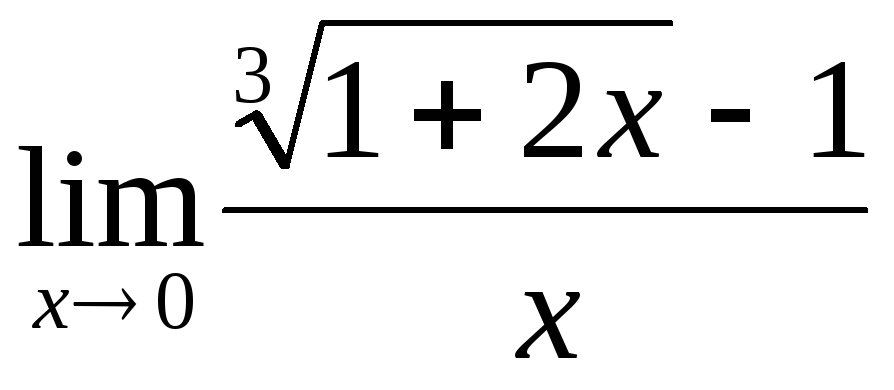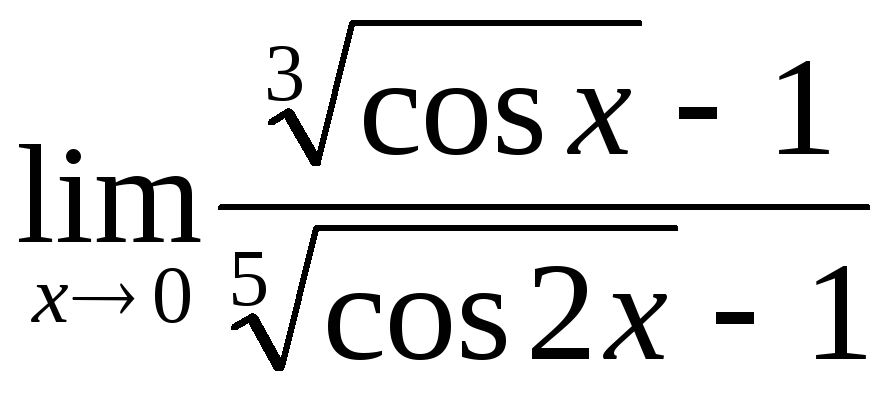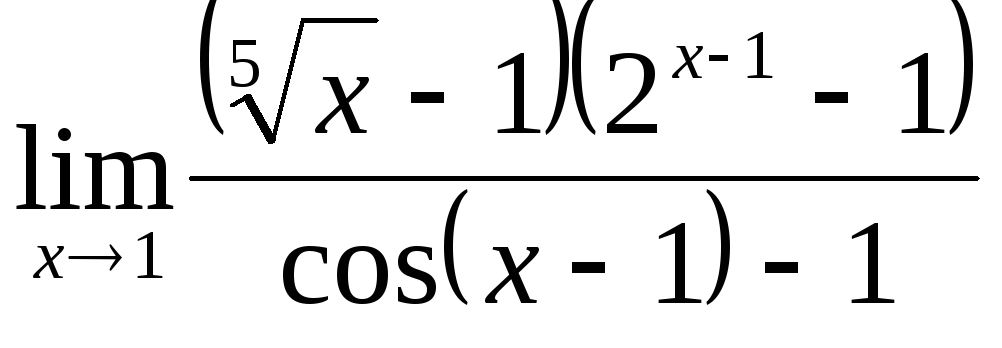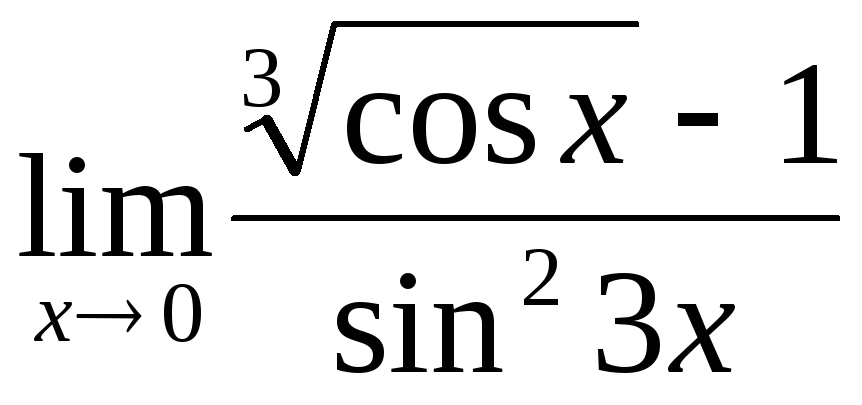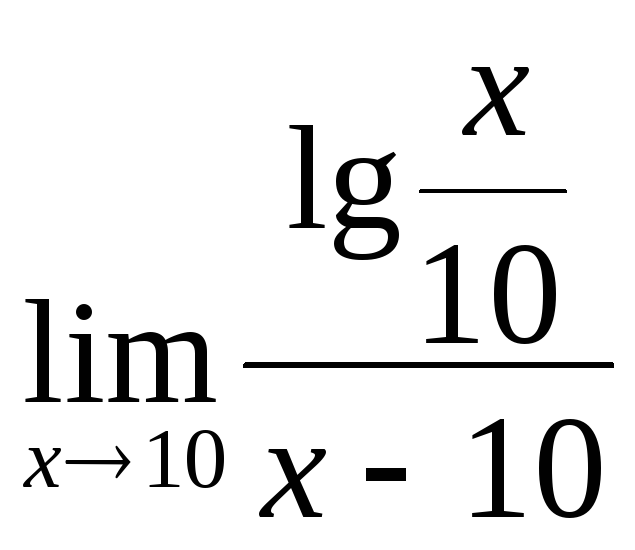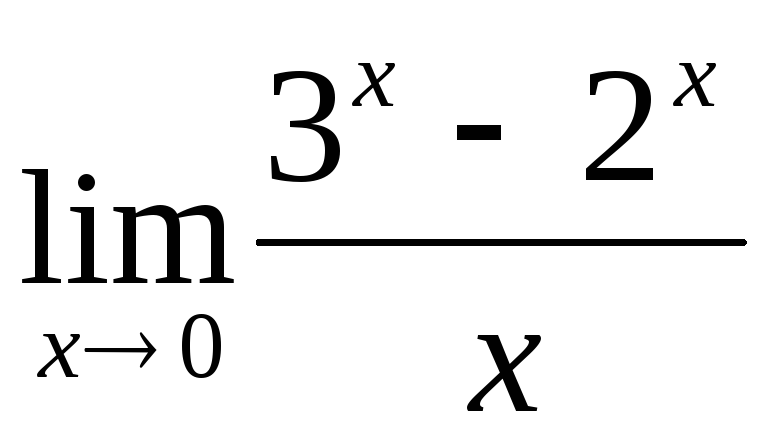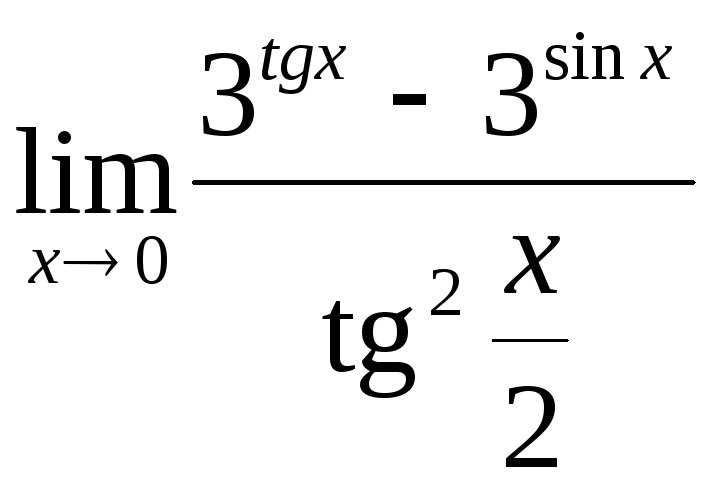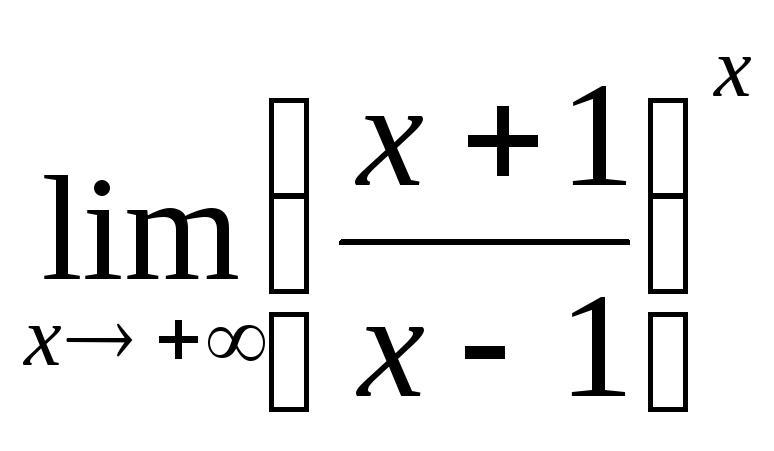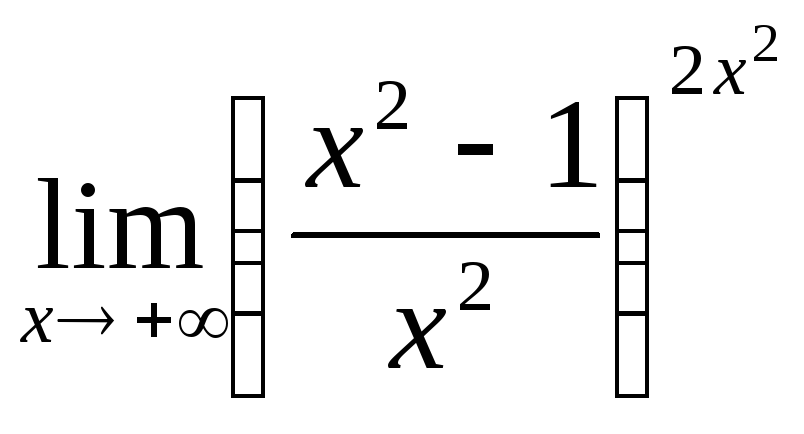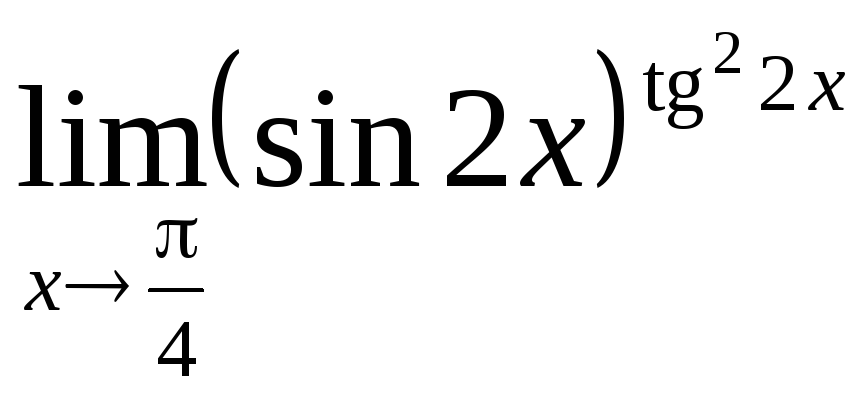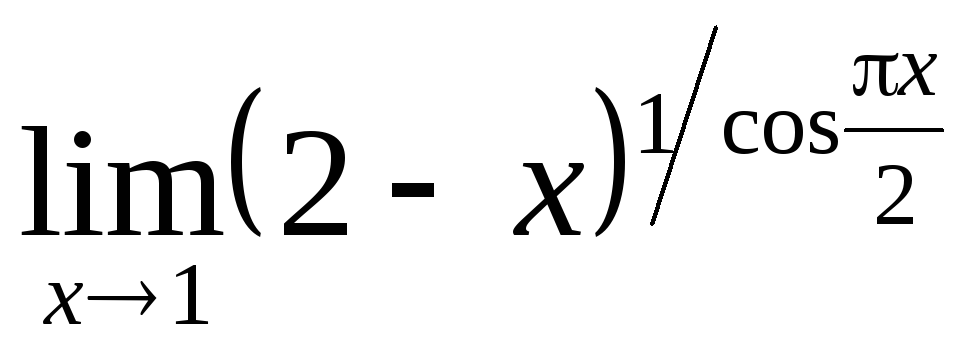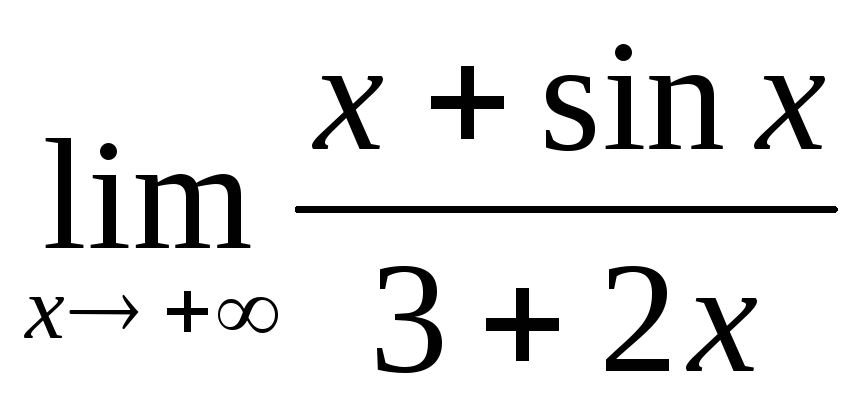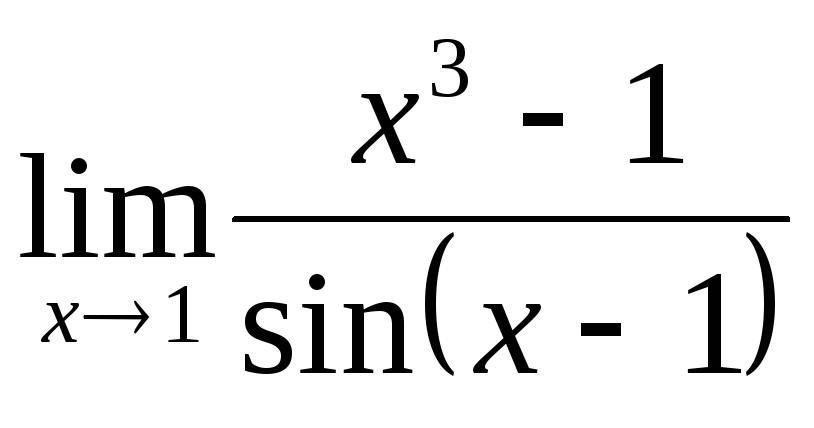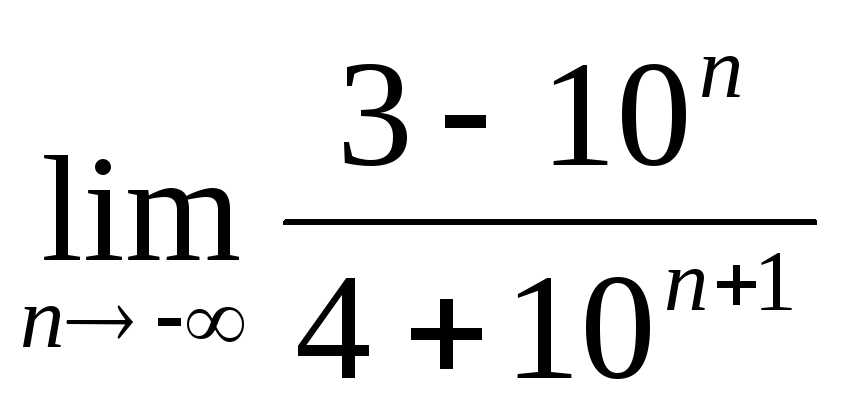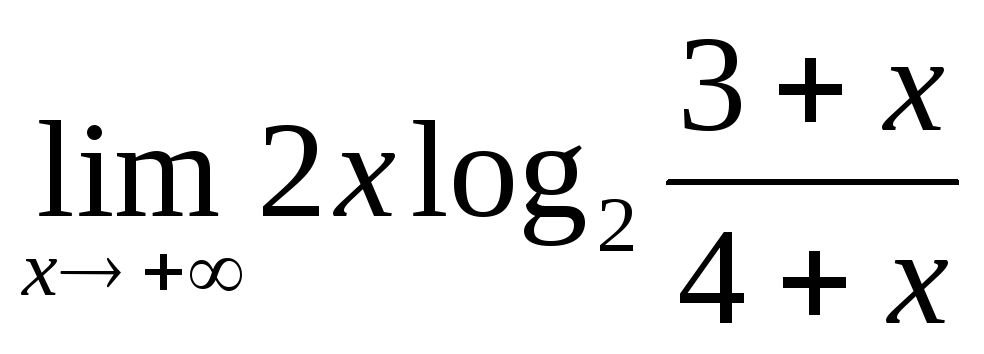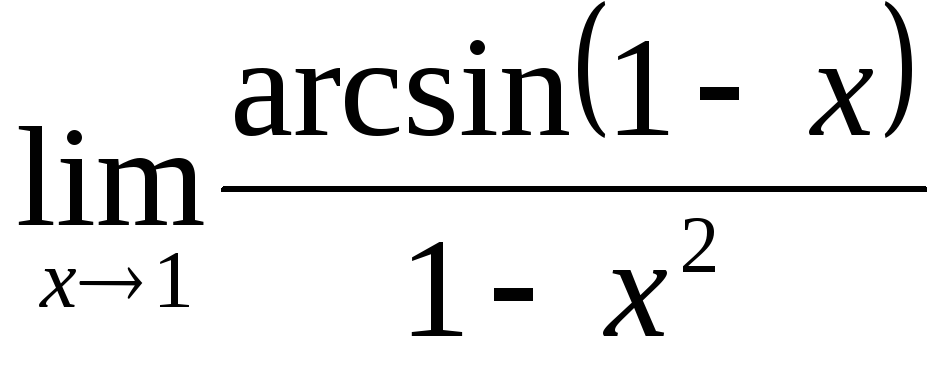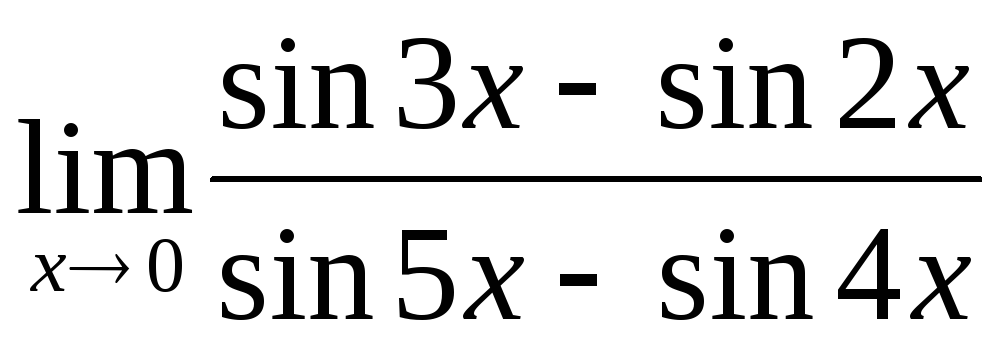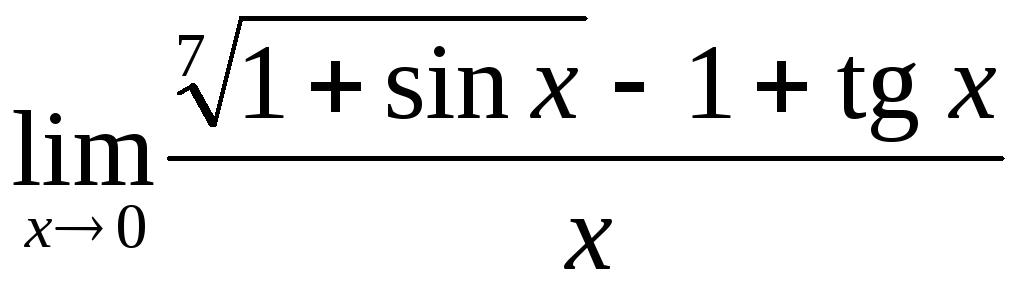
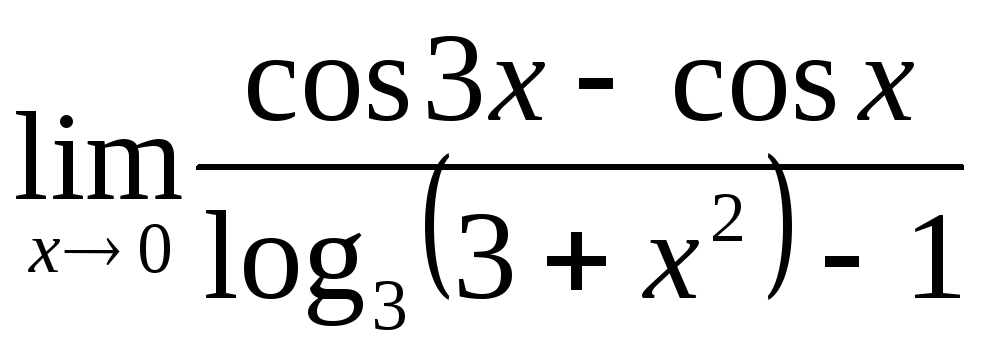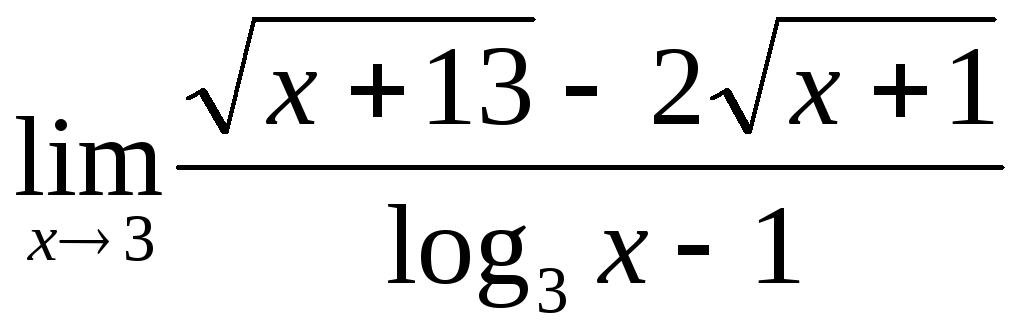
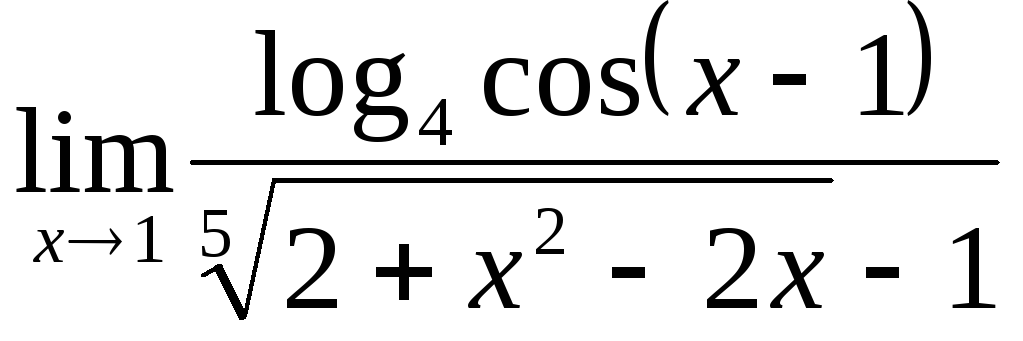
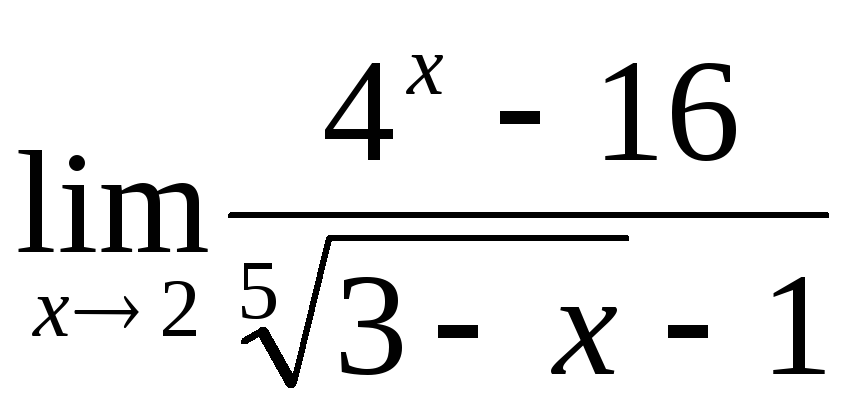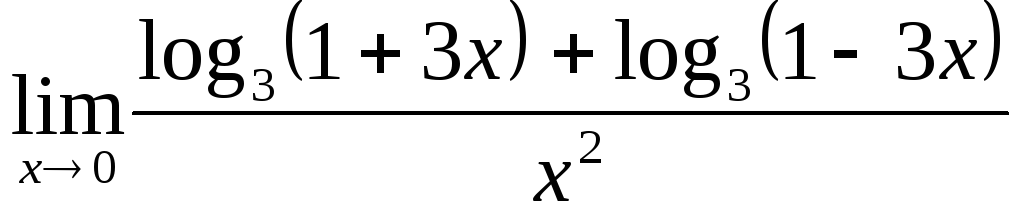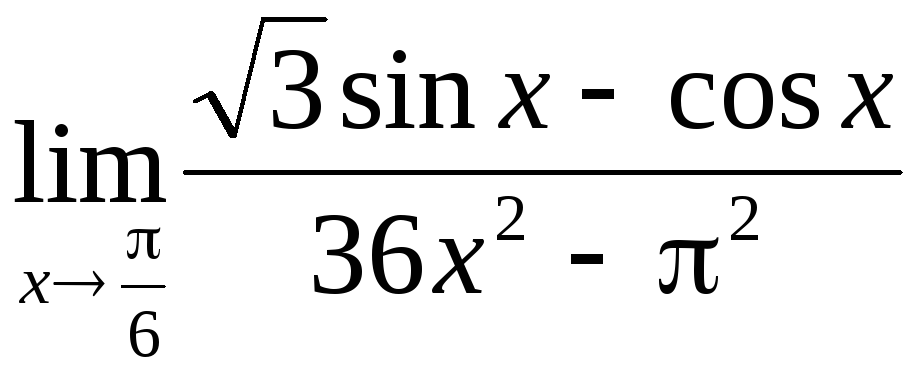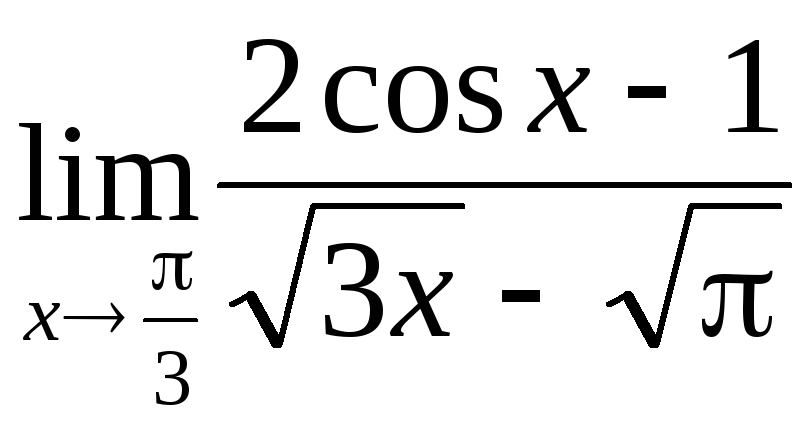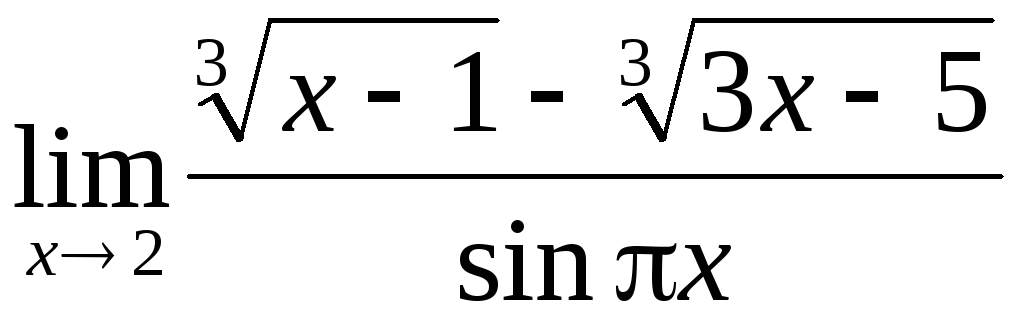
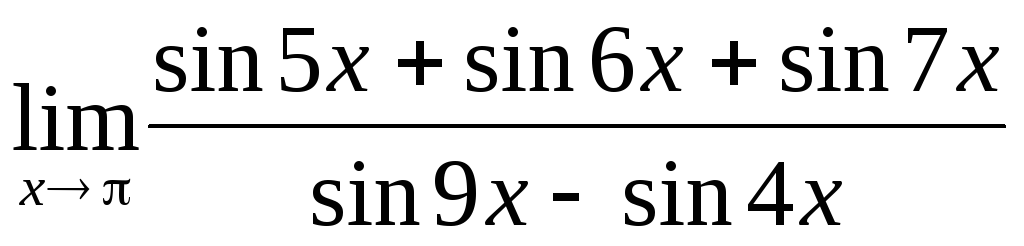
Ответы
1.
.
2.
.
3.
.
4.
.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
СОДЕРЖАНИЕ
Пределы последовательностей……………………………………….………3
Пределы функций. Точки разрыва функций………………………………12
Задания………………………………………………………………….…….17