
- •Пределы. Разрывы функций
- •2008 Удк 517
- •Пределы последовательностей
- •Признак существования конечного предела последовательности формулируется теоремой:
- •Решение. Подставляя в последовательность значение получим неопределенность. Для раскрытия неопределенности преобразуем знаменатель и воспользуемся формулами (7) и (12):
- •Пределы функций. Точки разрыва функции
- •Решение. А) Находим область определения функции:
- •Б) Находим область определения функции:
- •Решение. Функция непрерывна в точке , если выполняется условие (16). Проверим выполнение этого условия внутри каждого из заданных участков:
- •Задания
2082 МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Высшая математика»
Пределы. Разрывы функций
Задания и методические указания к выполнению типового расчета
для студентов первых курсов всех специальностей
очной формы обучения
Составители: Ф.С. Миронов
Н.М. Латыпова
Самара
2008 Удк 517
Пределы. Разрывы функций : задания и методические указания к выполнению типового расчета для студентов первых курсов всех специальностей очной формы обучения / составители : Ф.С. Миронов, Н.М. Латыпова. – Самара : СамГУПС, 2008. – 33 с.
Утверждены на заседании кафедры 06.09.2007г., протокол № 1.
Печатаются по решению редакционно-издательского совета университета.
Задания и методические указания составлены в соответствии с Государственными образовательными стандартами и действующей программой по высшей математике для всех специальностей. В методических указаниях даются необходимые краткие теоретические сведения и приводятся примеры решения заданий типового расчета по пределам и разрывам функций.
Составители: Миронов Ф.С.
Латыпова Н.М.
Рецензенты: д.п.н., зав. кафедрой «Высшая математика» СамГАСУ О.В. Юсупова
к.т.н., доцент кафедры «Высшая математика» СамГУПС О.Е. Лаврусь
Под редакцией В.А. Герасимова
Компьютерная верстка Р.Р. Абрамян
Подписано в печать 13.03.2008. Формат 60х84 1/16.
Бумага писчая. Печать оперативная. Усл.п.л. 2,0
Тираж 500 экз. Заказ № 23.
© Самарский государственный университет путей сообщения, 2008
ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
Пределы последовательностей
Определение
1. Переменная
![]() ,
принимающая некоторую последовательность
значений
,
принимающая некоторую последовательность
значений![]() ,
члены которой занумерованы всеми
натуральными числами и расположены в
порядке возрастания номеров, называетсявариантой
или последовательностью.
,
члены которой занумерованы всеми
натуральными числами и расположены в
порядке возрастания номеров, называетсявариантой
или последовательностью.
Варианта называется монотонно возрастающей, если
![]() (1)
(1)
Пример 1.
![]() ;
;
![]() - возрастающая варианта.
- возрастающая варианта.
Варианта называется монотонно убывающей, если
![]() (2)
(2)
Пример 2.
![]() ;
;
![]() - убывающая варианта.
- убывающая варианта.
Варианта называется немонотонной, если не выполняется условие (1) или (2).
Пример 3.
![]() ;
;
![]() - немонотонная последовательность.
- немонотонная последовательность.
Определение
2. Постоянное
число
![]() называетсяпределом
варианты
называетсяпределом
варианты
![]() ,
если для любого сколь угодно малого
числа
,
если для любого сколь угодно малого
числа![]() существует такой номер
существует такой номер![]() ,
что выполняется условие:
,
что выполняется условие:
![]() .
(3)
.
(3)
При
этом пишут:
![]() или
или![]() .
.
Определение
3. Последовательность
![]() называетсясходящейся,
если
называетсясходящейся,
если
![]() является конечным числом ирасходящейся,
если
является конечным числом ирасходящейся,
если
![]() или не существует предел
или не существует предел![]() .
.
В
примере 1
![]() является расходящейся последовательностью,
т.к.
является расходящейся последовательностью,
т.к.![]() .
.
В
примере 2
![]() является сходящейся последовательностью,
т.к.
является сходящейся последовательностью,
т.к.![]() .
.
В
примере 3
![]() является ограниченной последовательностью
(
является ограниченной последовательностью
(![]() не
превы-шает 1), но тем не менее расходящейся,
т.к. предел
не
превы-шает 1), но тем не менее расходящейся,
т.к. предел![]() не существует.
не существует.
Определение
4. Варианта
![]() называетсябесконечно
большой,
если для любого сколь угодно большого
числа
называетсябесконечно
большой,
если для любого сколь угодно большого
числа
![]() существует такой номер
существует такой номер![]() ,
что выполняется условие:
,
что выполняется условие:
![]() . (4)
. (4)
При
этом пишут:
![]() (
(![]() )
или
)
или![]() (
(![]() ).
).
Например,
в примере 1
![]() является бесконечно большой вариантой.
является бесконечно большой вариантой.
Определение
5. Варианта
![]() называетсябесконечно
малой,
если для любого сколь угодно малого
числа
называетсябесконечно
малой,
если для любого сколь угодно малого
числа
![]() существует такой номер
существует такой номер![]() ,
что выполняется условие:
,
что выполняется условие:
![]() . (5)
. (5)
Например,
в примере 2
![]() является бесконечно малой вариантой.
является бесконечно малой вариантой.
Теорема
1. Если для
двух вариант
![]() и
и![]() всегда выполняется условие
всегда выполняется условие![]() ,
причем каждая из них имеет конечный
предел
,
причем каждая из них имеет конечный
предел![]() и
и![]() ,
то и
,
то и![]() .
.
Теорема
2. Если для
вариант
![]() ,
,![]() ,
,![]() всегда выполняются неравенства
всегда выполняются неравенства![]() ,
причем варианты
,
причем варианты![]() и
и![]() стремятся к общему пределу
стремятся к общему пределу![]() ,
то и варианта
,
то и варианта![]() имеет тот же предел
имеет тот же предел![]() .
.
Если
варианты
![]() и
и![]() имеют конечные пределы
имеют конечные пределы![]() и
и![]() ,
то выполняются равенства:
,
то выполняются равенства:
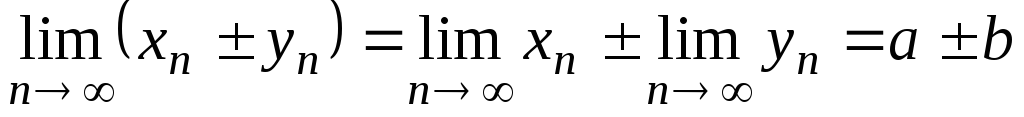 , (6)
, (6)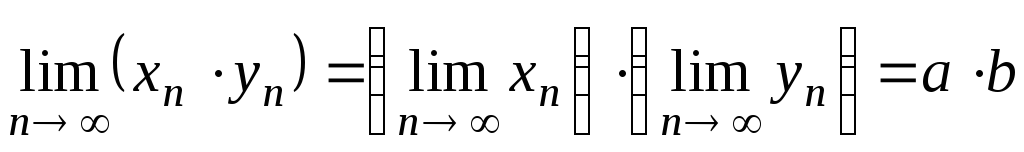 , (7)
, (7) . (8)
. (8)
