
- •Содержание рабочей программы
- •Рекомендуемая литература
- •Правила выполнения и оформления контрольных работ
- •9. Теоретический материал и методические указания к выполнению контрольных заданий приведены в работе [10] - му № 2312.
- •5.11. 5.12.
- •Задания на контрольную работу № 2 Введение в математический анализ
- •8.1. 8.2. 8.3
- •Примеры решения заданий контрольной работы № 1 Матрицы и определители
- •Системы линейных уравнений
- •Метод обратной матрицы
- •Метод Жордана-Гаусса последовательного исключения переменных
- •Элементы аналитической геометрии
- •Линии второго порядка
- •Примеры решения заданий контрольной работы № 2 Пределы
- •Непрерывность функции
- •Производная фунции и её геометрический смысл
- •Правило Лопиталя
- •Исследование функций и построение графиков
Примеры решения заданий контрольной работы № 1 Матрицы и определители
Сумма (разность) определяется только для матриц одинаковой размерности. Пусть
 .
Тогда
.
Тогда
 .
.
При умножении
матрицы А
на число
![]() нужно все элементы матрицыА
умножить на это число.
нужно все элементы матрицыА
умножить на это число.
Если
![]()
![]() ,
то
,
то![]() .
.
Произведением
матрицы
![]() на матрицу
на матрицу![]() называется матрица
называется матрица![]() ,
элементы которой находятся по формуле
,
элементы которой находятся по формуле![]() .
В общем случае
.
В общем случае![]()
Пусть
![]() ,
, .
.
Имеем: ,
где
,
где
![]()
![]() следовательно
следовательно
![]() .
.
Определителем
второго
порядка называется число,
равное
 .
(1.1)
.
(1.1)
Примеры.
1)
 ;
2)
;
2) .
.
Определителем третьего порядка называется число, равное сумме произведений элементов его первой строки на их алгебраические дополнения.
 .
(1.2)
.
(1.2)
Аналогично определяются определители более высоких порядков.
![]()
Вычислим определитель, разложив его по элементам первой строки:
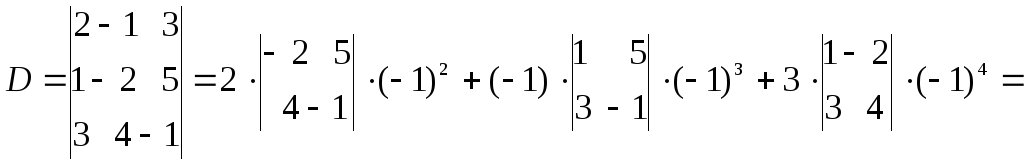
![]() .
.
Определители третьего порядка можно вычислить и по правилу треугольников (правилу Саррюса) по схеме:
 .
(1.3)
.
(1.3)
Пример.
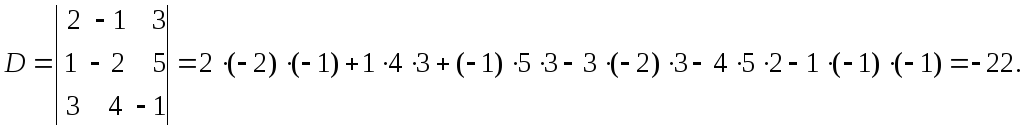
Системы линейных уравнений
Метод Крамера
Пример. Решить систему линейных уравнений по формулам Крамера
 .
.
Вычислим определитель
системы
![]()

Вычислим определители D1, D2, D3, заменяя в определителе D элементы первого, второго и третьего столбцов соответственно элементами столбца из свободных членов.
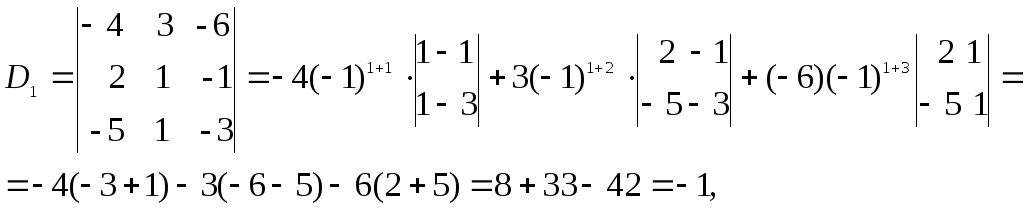
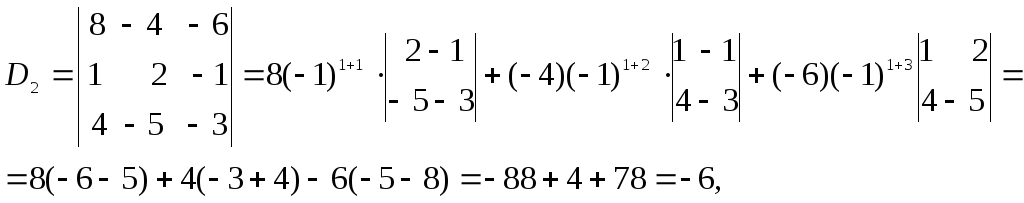
 .
.
Таким образом,
![]() ,
х2=
,
х2=![]() ,
,![]() .
.
Итак,
х1=1, х2=6, х3=5.
Метод обратной матрицы
Определение.
Матрица А
называется невырожденной, если D=det
А![]() 0.
0.
Каждая невырожденная
матрица А
имеет обратную
![]() ,
причем для матрицы
,
причем для матрицы![]() третьего порядка с элементами
третьего порядка с элементами![]() :
: обратная матрица
обратная матрица![]() имеет вид:
имеет вид:
 , (1.4)
, (1.4)
где А11,
А12
,…, А33
–
алгебраические
дополнения соответствующих элементов
![]() матрицы
матрицы![]() ,
располагаемые по столбцам в новой
матрице.
,
располагаемые по столбцам в новой
матрице.
Пример. Решить систему уравнений матричным методом:
 .
Имеем: А=
.
Имеем: А=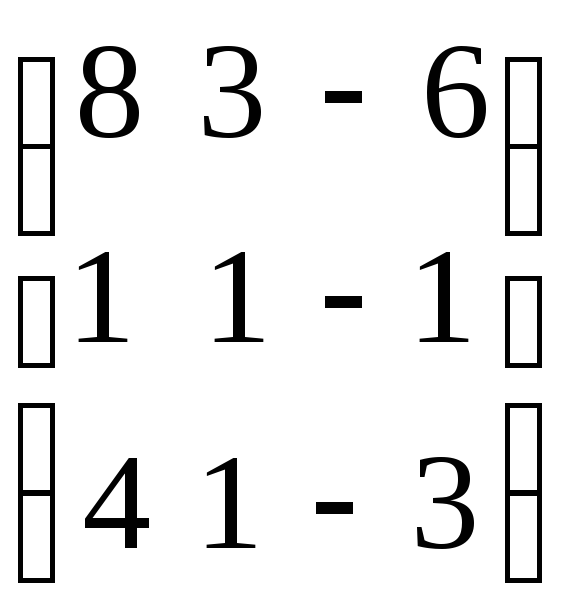 ,Х=
,Х=![]() ,Н=
,Н=![]() .
.
![]() ,
,
![]() .
.
Для нахождения обратной матрицы А-1 вычисляем все алгебраические дополнения элементов матрицы А:
![]() ,
,
![]() ,
, ,
,
![]() ,
,
![]() ,
, ,
,
![]() ,
,
![]() ,
,![]() .
.
Составляем обратную матрицу (1.4):
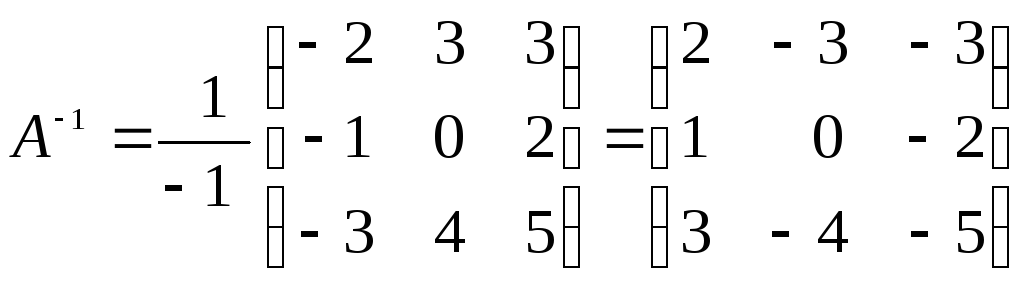 .
.
Тогда
 .
.
Таким образом, х1=1, х2=6, х3=5.
Метод Жордана-Гаусса последовательного исключения переменных
Пример. Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.

Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем расширенную матрицу системы:

![]()

![]()

![]()
![]()

![]()

![]()

Поясним сделанные преобразования:
Первую строку умножим последовательно на (- 2), (-3), (-4) и прибавим ко второй, третьей и четвертой строкам соттветственно.
Вторую строку умножаем на (-1), (-2) и прибавим к третьей и четвертой строке соответственно.
Поменяем местами вторую и четвертую строчку.
Вторую строку умножаем на 2 и на (-3) и прибавим к первой и третьей строке соответственно. Удаляем четвертую – нулевую строку.
Третью строку умножаем на на (-1) и на (-3) и прибавляем ко второй и первой строке соответственно.
Используя последнюю матрицу, эквивалентную исходной, получаем равносильную систему уравнений следующего вида:
![]()
 х1+
х1+![]() +1,2х4
= 1
+1,2х4
= 1
х2+ +0,4х4 = 3
х3+ −1,4х4 =− 2.
Переменные![]() х1,
х2,
х3
х1,
х2,
х3![]() назовём
базисными, переменную х4
−
свободной. Полагая х4=0,
непосредственно находим базисное
решение: х1=1,
х2=3,
х3=−2.При
х4=5,
получим частное решение: х3=5,
х2=1,
х1=−5.
При х4=
t,
где
t
назовём
базисными, переменную х4
−
свободной. Полагая х4=0,
непосредственно находим базисное
решение: х1=1,
х2=3,
х3=−2.При
х4=5,
получим частное решение: х3=5,
х2=1,
х1=−5.
При х4=
t,
где
t![]()
R,
получим общее решение системы:
R,
получим общее решение системы:
х 1=1-1,2
t
1=1-1,2
t
х2=3-0,4 t
х3=-2+1,4 t.
