5.11. 5.12.

_{5.13. 5.14.}

_{5.15. 5.16.}

_{5.17. 5.18.}

_{5.19. 5.20.}

_{5.21. 5.22.}

_{5.23. 5.24.}

_{5.25. 5.26.}

_{5.27. 5.28.}

5.29. 5.30..

№№ 6.1-6.30. Приведите к каноническому виду уравнение 2-го порядка и постройте линию, заданную этим уравнением.

№ вар.	6.1	6.2	6.3	6.4	6.5	6.6	6.7	6.8	6.9	6.10	6.11	6.12	6.13	6.14	6.15
A	4	1	2	1	1	3	16	9	0	2	1	-1	0	2	3
B	9	1	5	-6	-1	-4	5	-4	-3	0	2	2	1	1	-2
C	32	-4	8	-12	0	-18	64	18	4	-8	6	6	1	8	12
D	-54	6	-10	36	2	-16	-30	24	12	-1	8	16	2	6	4
E	109	4	-17	-30	-17	-5	29	-63	-12	11	9	-1	4	-3	4

№ вар.	6.16	6.17	6.18	6.19	6.20	6.21	6.22	6.23	6.24	6.25	6.26	6.27	6.28	6.29	6.30
A	1	2	1	0	4	-2	2	1	2	0	4	1	0	2	3
B	0	4	-3	-2	2	3	0	4	-4	-2	1	-2	3	4	0
C	2	4	4	3	8	8	4	2	4	3	12	4	6	-8	6
D	-2	4	12	8	4	6	4	8	8	6	6	8	-6	8	-3
E	3	-5	-11	-8	-2	-17	6	-11	-20	-4,5	2	-6	9	11	5

Задания на контрольную работу № 2 Введение в математический анализ

№№ 7.1-7.30. Найдите пределы функций, не используя правило Лопиталя.

7.1. а) ,b) , c)

при x₀=1; x₀=¥

7.2. а) , b) , c) ;

при x₀=2; x₀=¥.

7.3. а) ,b) , c) ;

при x₀=-4; x₀=¥.

7.4. а) ,b) , c) ;

при x₀=5; x₀=¥

7.5. а) ,b) , c) ;

при x₀=-2; x₀=¥.

7.6. а) ,b) , c) ;

при x₀=4; x₀=¥.

7.7. а) ,b) , c) ;

при x₀=-1; x₀=¥.

7.8. а) ,b) , c) ;

при x₀=3; x₀=¥.

7.9. а) ,b) , c) ;

при x₀=-3; x₀=¥.

7.10. а) ,b) , c) ;

при x₀=-5; x₀=¥.

7.11. a) , b), c);

при

7.12. a) , b) , c) ;

при

7.13. a) , b), c);

при

7.14. a) , b), c);

при

7.15. a) , b), c);

при

7.16. a) , b), c);

при

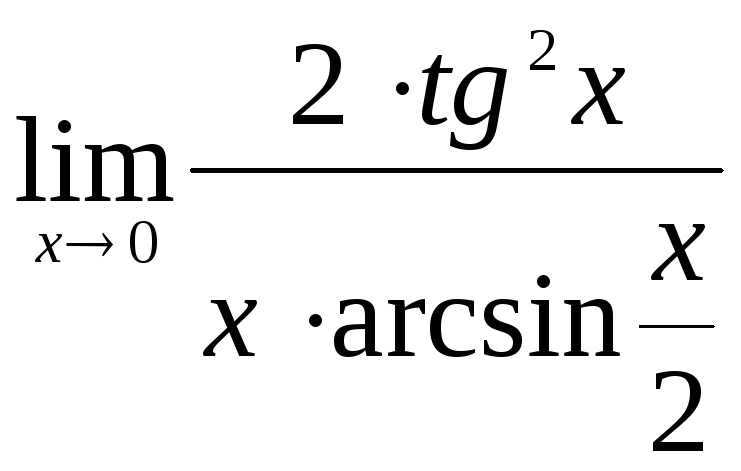7.17. a) , b), c);

при

7.18. a) , b), c);

при

7.19. a) , b), c);

при

7.20. a) , b), c);

при

7.21. a) , b) , c) ;

при

7.22. a) , b) , c) ;

при .

7.23. a) , b) , c) ;

при .

7.24. a) , b) , c) ;

при .

7.25. a) , b) , c) ;

при .

7.26. a) , b) , c) ;

при .

7.27. a) , b) , c) ;

при .

7.28. a) , b) , c) ;

при .

7.29. a) ,b) ,c) ;

при .

7.30. a) ,b) ,c) .

при .

№№ 8.1-8.30. Исследуйте данную функцию на непрерывность и постройте ее график.

8.1. 8.2. 8.3

8.4. 8.5. 8.6 8.7. 8.8. 8.9.

8.10. 8.11. 8.12.

_{8.13. 8.14. 8.15.}

_{8.16.8.17.8.18.}

_{8.19.8.20.8.21.}

_{8.22. 8.23. 8.24.}

8.25. 8.26. 8.27.

₈

8.30

.28. 8.29.

Дифференциальное исчисление функций одной переменной

№№ 9.1-9.30. Найдите дифференциалы функций.

9.1. а) ; b) ; c)d).

9.2. a) ; b); c);d).

9.3.a); b); c); d).

9.4. a) ; b)c); d).

9.5. a) ; b)c); d).

9.6. a) ; b)c);d).

9.7. a) ; b);c);d).

9.8. a) ; b)c);d).

9.9.a);b)c); d).

9.10. a) ; b)c); d).

9.11. a) ; b) ; c) ; d) .

9.12. a) ; b) ; c) ; d) .

9.13. а);b) ;c);d).

9.14. а);b) ;c);d).

9.15. а);b);c);d).

9.16. а) ;b);c);d).

9.17. а);b);c);d).

9.18. а) ;b);c);d).

9.19. а);b);c) ; d)

9.20. а);b) ;c);d).

9.21. а);b);c);d).

9.22. а);b);c);d).

9.23. а);b);c);d).

9.24. а);b);c);d)

9.25. а);b);c) ;d).

9.26. а) b) ;c);d).

9.27. а);b);c);d) .

9.28. а) ;b);c);d) .

9.29. а) ;b);c);d) .

9.30. а) ;b);c);d).

№№ 10.1-10.30. Составьте уравнения касательной и нормали к кривой в точке с абсциссойx₀.

№ вар.	10.1	10.2	10.3	10.4	10.5	10.6	10.7	10.8	10.9	10.10	10.11	10.12	10.13	10.14	10.15
a	1	-1	2	-2	3	-3	1	-1	2	3	-3	-2	1	-1	2
b	-4	6	8	10	-6	12	6	4	10	12	6	8	8	2	6
c	2	-4	9	-8	4	-8	7	-2	5	10	-1	-6	13	2	3
	2,5	2	-1,5	2	1,5	2,5	-2	3	-4	-1,5	1,5	2,5	-5	1,5	-1
№ вар.	10.16	10.17	10.18	10.19	10.20	10.21	10.22	10.23	10.24	10.25	10.26	10.27	10.28	10.29	10.30
a	-2	3	-3	1	1	1	1	1	-1	-3	-2	3	2	2	-2
b	-8	-12	-6	4	-4	-8	-10	-6	10	-4	6	12	-4	-8	-10
c	-5	10	0	2	1	16	25	5	-20	0	-3	10	5	6	-5
	-2,5	2,5	-1,5	-3	3	3	4	2	4	1	1	-1,5	1,5	1,5	-4

№№ 11.1-11.30. Найдите пределы функций с помощью правила Лопиталя. Условие взять из заданий 7.1-7.30 (примеры a и b).

№№ 12.1-12.30. Исследуйте функцию методами дифференциального исчисления и постройте ее график.

12.1. ;12.2. ;12.3. ;12.4. ;

12.5. ;12.6. ;12.7. ;12.8. ;

12.9. ;12.10. ;12.11. 12.12. ;

12.13. ; 12.14. ; 12.15. ; 12.16. ;

12.17. ; 12.18. ; 12.19. ; 12.20. ;

12.21. ; 12.22. ; 12.23. ; 12.24. ;

12.25. ; 12.26. ; 12.27. ; 12.28. ;

12.29. ; 12.30. .